[알고리즘/ 그래프] 최소 스패닝 트리 - 크루스칼(Kruskal)과 프림(Prim) 알고리즘 (Java)
스패닝 트리 또는 신장 트리
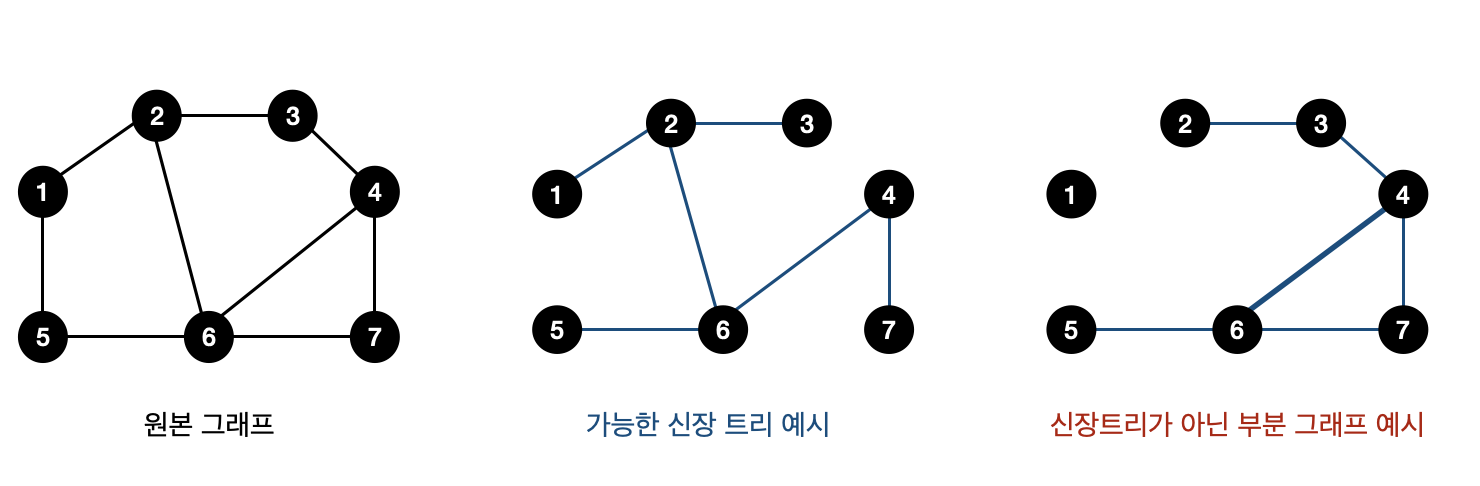
어떤 무향 그래프의 스패닝 트리는 원래 그래프의 정점 전부와 간선의 부분 집합으로 구성된 부분 그래프이다. 이때 스패닝 트리에 포함된 간선들은 정점들을 트리 형태로 전부 연결해야 한다.
- 트리 형태여야 한다는 말은 선택된 간선들이 사이클을 이루지 않는다는 뜻이며, 정점들이 꼭 부모-자식 관계로 연결될 필요는 없다는 데 유의하자.
즉, 스패닝 트리는 그래프에서 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미한다.
- 모든 노드가 포함되어 서로 연결되면서 사이클이 존재하지 않는다는 조건은 트리의 조건이기도 하다.
최소 스패닝 트리 (MST)
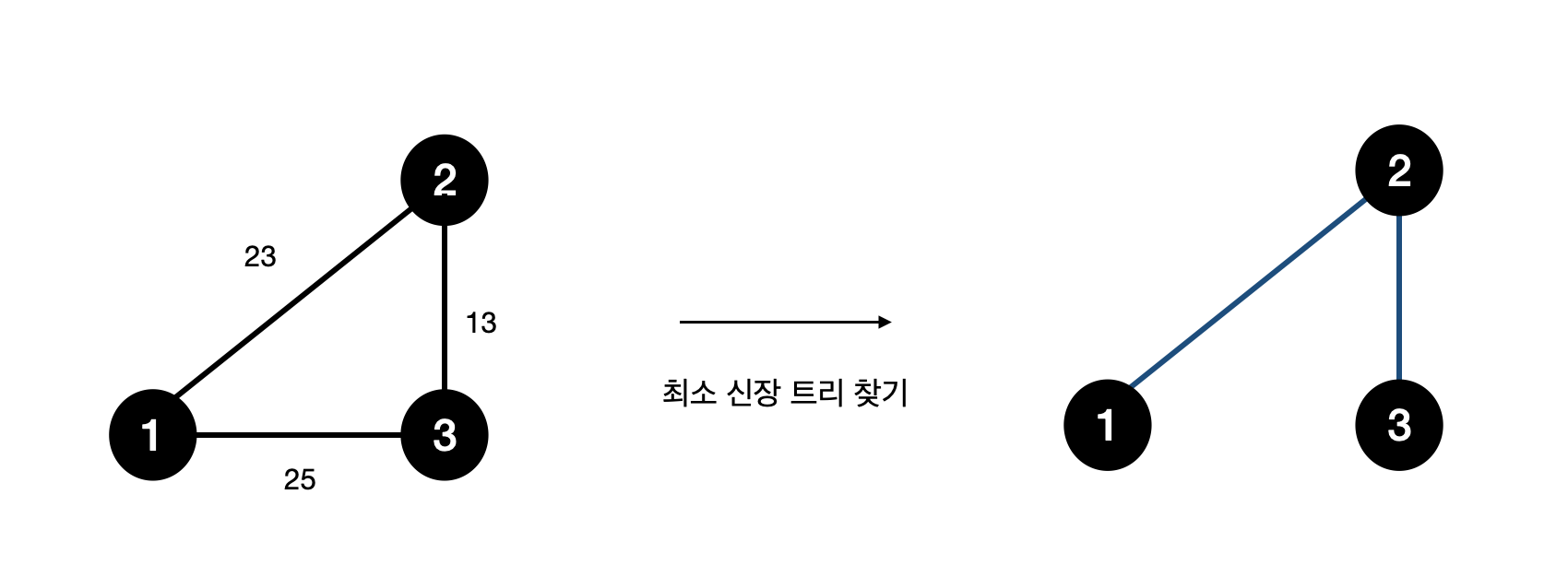
최소 스패닝 트리란 최소한의 비용으로 구성되는 스패닝 트리를 말한다. 두 가지 유명한 알고리즘으로 크루스칼과 프림이 있다.
- 크루스칼 알고리즘은 상호 배타적 집합 자료구조(유니온파인드)의 좋은 사용 예이다.
- 프림 알고리즘은 다익스트라 알고리즘과 거의 비슷한 형태를 띠고 있다.
크루스칼 알고리즘 (Kruskal Algorithm)
대표적인 최소 신장 트리 알고리즘으로 간선의 가중치의 합이 최솟값이 되도록 모든 노드를 연결시킨다. 크루스칼 알고리즘은 가중치가 가장 작은 간선일 수록 최소 스패닝 트리에 포함된다는 발상으로 인해 만들어졌다.
- 그래서 그래프의 모든 간선을 가중치의 오름차순으로 정렬한 뒤, 스패닝 트리에 하나씩 추가해 간다.
- 물론 가중치가 작다고 해서 무조건 간선을 트리에 더하는 것은 아니다. 자칫하다가는 싸이클을 이룰 수도 있기 때문이다.
따라서, 결과적으로 사이클이 생기는 간선은 고려에서 제외해야 한다. 크루스칼 알고리즘은 모든 간선을 한 번씩 검사하고 난 뒤 종료한다.
동작 과정
- 간선 데이터를 비용에 따라 오름차순으로 정렬한다.
- 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인한다.
- 사이클이 발생하지 않는 경우 최소 신장 트리에 포함시킨다.
- 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않는다
- 모든 간선에 대하여 2번의 과정을 반복한다.
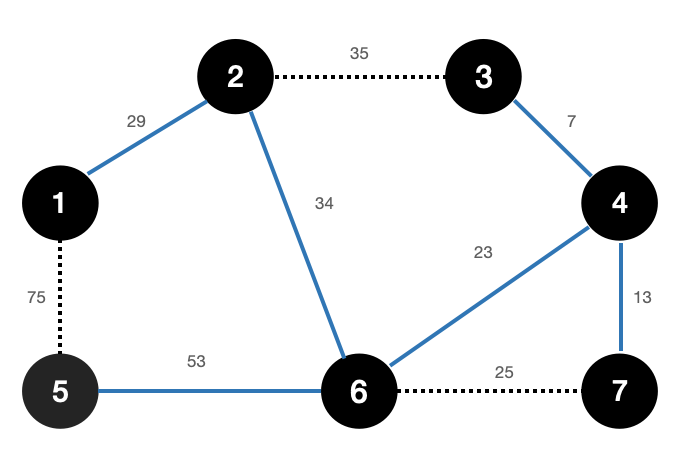
| 간선 | (1,2) | (1,5) | (2,3) | (2,6) | (3,4) | (4,6) | (4,7) | (5,6) | (6,7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | step 5 | step 9 | step 7 | step 6 | step 1 | step 3 | step 2 | step 8 | step 4 |
크루스칼 알고리즘 코드
크루스칼 알고리즘은 상호 배타적 집합 자료구조(Union-Find)를 활용해 구현해주면 된다. 이 자료구조에서 한 집합은 그래프의 한 컴포넌트를 표현한다.
- 그래서 새 간선을 추가할 때마다 사이클이 생기는지 확인하려면 두 정점이 이미 같은 집합에 속해있는지 확인하면 되고,
- 간선을 트리에 추가할 경우에는 이들이 포함된 두 집합을 합치면 된다.
class Node implements Comparable<Node>{
int to;
int from;
int value;
public Node(int to, int from, int value) {
this.to = to;
this.from = from;
this.value = value;
}
@Override
public int compareTo(Node o) {
return this.value - o.value;
}
}
public class Main {
private static int n;
private static int[] parents;
public static void main(String[] args) {
n = 7;
int[][] graph = {{1,2,29}, {1,5,75},{2,3,35},{2,6,34}, {3,4,7},{4,6,23},
{4,7,13}, {5,6,53}, {6,7,25}};
parents = new int[n + 1];
for (int i=1; i<n+1; i++) {
parents[i] = i;
}
Queue<Node> pq = new PriorityQueue<>();
for(int i=0; i<graph.length; i++) {
int to = graph[i][0];
int from = graph[i][1];
int value = graph[i][2];
// 우선순위 큐는 자동으로 간선 비용순(오름차순)으로 정렬된다.
pq.add(new Node(to, from, value));
}
int size = pq.size();
int total =0;
// 간선 하나씩 조회 (비용이 작은 간선부터)
for(int i=0; i< size; i++) {
Node node = pq.poll();
int rx = find(node.to);
int ry = find(node.from);
// 사이클이 발생하지 않는 경우에만 집합에 포함
if(!isSameParent(rx, ry)) {
total += node.value;
union(node.to,node.from);
}
}
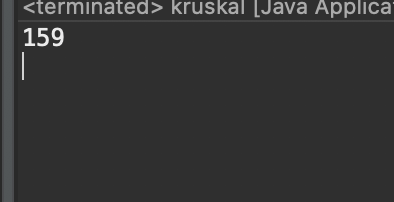
System.out.println(total);
}
static int find(int x) {
if (parents[x] == x) {
return x;
}
return parents[x] = find(parents[x]);
}
static void union(int x, int y) {
x = find(x);
y = find(y);
// 더 find 값으로 부모 노드 설정
if (x < y) {
parents[y] = x;
}
else {
parents[x] = y;
}
}
static boolean isSameParent(int x, int y) {
if(rx == ry) return true;
return false;
}
}
간선 비용이 낮은 순으로 오름차순으로 정렬 후 간선을 하나씩 조회하여 사이클이 발생하지 않게 집합(union)을 구하면 아래 그림의 트리와 같이 최소 신장 트리가 나온다.
프림 알고리즘 (Prim Algorithm)
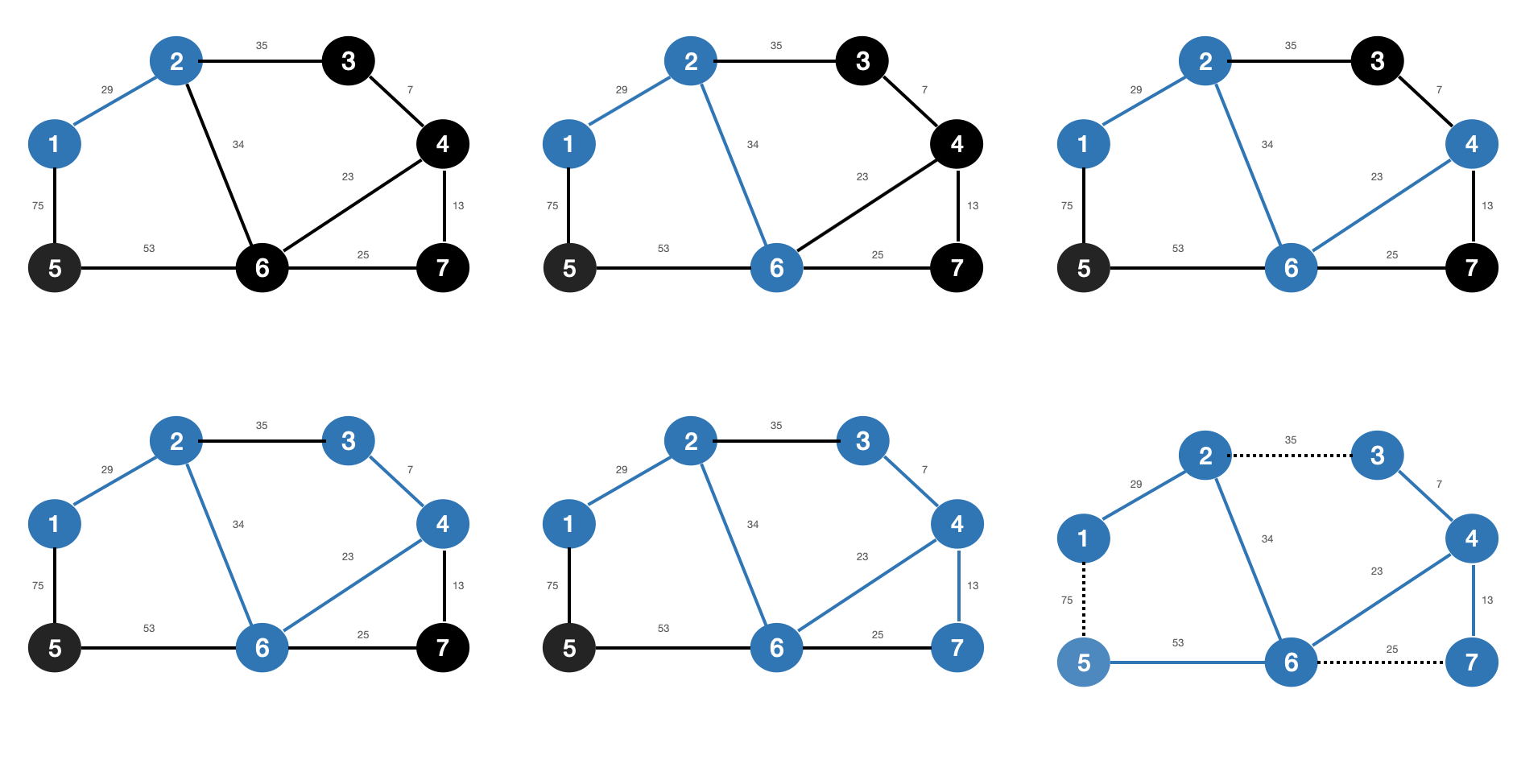
프림 알고리즘은 최소 신장트리를 구하는 또 하나의 알고리즘으로, 하나의 시작 정점을 기준으로 가장 작은 간선과 연결된 정점을 선택하여 스패닝 트리가 될 때까지 모든 노드를 연결시킨다. 따라서 항상 선택된 간선들은 중간 과정에서도 항상 연결된 트리를 이루게 된다.
- 이미 만들어진 트리에 인접한 간섭만을 고려한다는 점을 제외하면 프림은 크루스칼과 완전히 똑같다. 프림 알고리즘 또한 선택할 수 있는 간선들 중 가중치가 가장 작은 간선을 선택하는 과정을 반복하기 때문이다.
동작 과정
프림 알고리즘 동작과정은 간단하다.
- 임의의 간선을 선택한다.
- 선택한 간선의 정점으로부터 가장 낮은 가중치를 갖는 정점을 선택한다.
- 모든 정점에 대하여 2번의 과정을 반복한다.
프림 알고리즘 코드
프림 알고리즘 구현은 간단하다. 각 정점이 트리에 포함되었는지 여부를 나타내는 불린 값 배열 visited[]을 두고, 각 차례마다 최적의 간선을 찾아 다음으로 트리에 추가해주면 된다.
최적의 간선을 찾는 법은 트리와 이 정점을 연결하는 간선의 최소 가중치를 저장하는 배열 minWeight[]를 선언하여 사용해주면 되지만 그냥 다익스트라 알고리즘처럼 우선순위 큐를 사용하면 각 정점의 번호를 minWeight[]이 증가하는 순으로 담고있게 되므로 따로 배열 선언을 해주지 않고 구현이 가능하다.
class Node implements Comparable<Node>{
int to;
int value;
public Node(int to, int value) {
this.to = to;
this.value = value;
}
@Override
public int compareTo(Node o) {
return this.value - o.value;
}
}
public class Main {
static int total;
static List<Node>[] list;
static boolean[] visited;
public static void main(String[] args){
int v = 7;
int[][] graph = {{1,2,29}, {1,5,75},{2,3,35},{2,6,34}, {3,4,7},{4,6,23},
{4,7,13}, {5,6,53}, {6,7,25}};
list = new ArrayList[v+1];
visited = new boolean[v+1];
for(int i=1; i<v+1; i++) {
list[i] = new ArrayList<>();
}
for(int i=0; i<graph.length; i++) {
int a = graph[i][0];
int b = graph[i][1];
int w = graph[i][2];
list[a].add(new Node(b,w));
list[b].add(new Node(a,w));
}
prim(1);
System.out.println(total);
}
static void prim(int start) {
Queue<Node> pq = new PriorityQueue<>();
pq.add(new Node(start,0));
while(!pq.isEmpty()) {
Node p = pq.poll();
int node = p.to;
int weight = p.value;
if(visited[node]) continue;
// 선택한 간선의 정점으로부터 가장 낮은 가중치 갖는 정점 선택
visited[node]= true;
total += weight;
for(Node next : list[node]) {
if(!visited[next.to]) {
pq.add(next);
}
}
}
}
}
낮은 간선을 가진 정점을 기준으로 위주로 탐색하면 최소 신장 트리를 구할 수 있다.
크루스칼 vs 프림
| 크루스칼 알고리즘 | 프림 알고리즘 | |
| 탐색 방법 | 간선 위주 | 정점 위주 |
| 탐색 과정 | 시작점 따로 지정없이 최소 비용의 간선을 차례대로 대입하면서 사이클이 이루어지기 전까지 탐색 | 시작점을 지정한 후 가까운 정점을 선택하면서 모든 정점을 탐색 |
| 사용 | 간선의 개수가 적은 경우 크루스칼 알고리즘이 용이 | 간선의 개수가 많은 경우에는 정점 위주 탐색인 프림이 용이 |
| 시간복잡도 | O(ElogV) | O(ElogV) |
✱ 참고사이트
종만북