[알고리즘] 분할정복 알고리즘 정리 (합병 정렬, 퀵 정렬, 이진 탐색) (Java)

Dot Algo∙ DS/알고리즘 개념

[알고리즘] 분할정복 알고리즘 정리 (합병 정렬, 퀵 정렬, 이진 탐색) (Java)

루지 2021. 5. 30. 16:46

분할정복(divide and conquer) 알고리즘

분할정복 알고리즘 (Divide and conquer algorithm)은 그대로 해결할 수 없는 문제를 작은 문제로 분할하여 문제를 해결하는 방법이다. 대표적인 예로는 정렬 알고리즘 중에서 퀵 정렬이나 합병 정렬과 이진 탐색, 선택 문제, 고속 푸리에 변환(FFT) 문제들이 대표적이다.

정렬 알고리즘 비교

선택 정렬과 삽입 정렬의 최대 실행시간은 O(n^2)이다. 입력하는 배열의 크기가 크다면 이 알고리즘으로 정렬하는데 매우 오랜 시간이 걸릴 수 있다.
반면 분할정복 알고리즘을 사용하는 합병 정렬의 실행시간은 모든 경우에 대해 O(nlgn)으로 , 퀵 정렬은 최대 O(n^2)이지만 최선이나 평균의 경우 O(nlgn)으로 비교적 빠른 시간을 갖는 것을 볼 수 있다.

정렬 알고리즘	최대 실행 시간	최소 실행 시간	평균 실행 시간
선택 정렬	O(n^2)	O(n^2)	O(n^2)
삽입 정렬	O(n^2)	O(n)	O(n^2)
합병 정렬	O(nlgn)	O(nlgn)	O(nlgn)
퀵 정렬	O(n^2)	O(nlgn)	O(nlgn)

분할정복 설계

1) Divide

원래 문제가 분할하여 비슷한 유형의 더 작은 하위 문제로 분할이 가능할 때 까지 나눈다.

2) Conquer

각 하위 문제를 재귀적으로 해결한다. 하위 문제의 규모가 나눌 수 없는 단위가 되면 탈출 조건을 설정하고 해결한다.

3) Combine

Conquer한 문제들을 통합하여 원래 문제의 답을 얻어 해결한다.

🖋 Divide를 제대로 나누면 Conquer과정은 자동으로 쉬워진다. 그래서 Divide를 잘 설계하는 것이 중요!

🖋 분할정복 알고리즘은 재귀 알고리즘이 많이 사용되는데, 이 부분에서 분할정복 알고리즘의 효율성을 깎아내릴 수 있다.

☛ 분할정복 알고리즘은 최소한 두 개의 하위 문제를 생성하므로 재귀 호출을 여러번 실행한다.

분할정복 특징 및 장단점

분할된 작은 문제는 원래 문제와 성격이 동일하다 -> 입력 크기만 작아짐
분할된 문제는 서로 독립적이다(중복 제거 X) -> 순환적 분할 및 결과 결합 가능

분할정복은 Top-down방식으로 재귀 호출의 장단점과 똑같다고 보면 된다.

장점	단점
∙ Top-down 재귀방식으로 구현하기 때문에 코드가 직관적이다. ∙ 문제를 나누어 해결한다는 특징상 병렬적으로 문제를 해결할 수 있다.	∙ 재귀 함수 호츨로 오버헤드가 발생할 수 있다. ∙ 스택에 다량의 데이터가 보관되는 경우 오버플로우가 발생할 수 있다.

합병 정렬

하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.

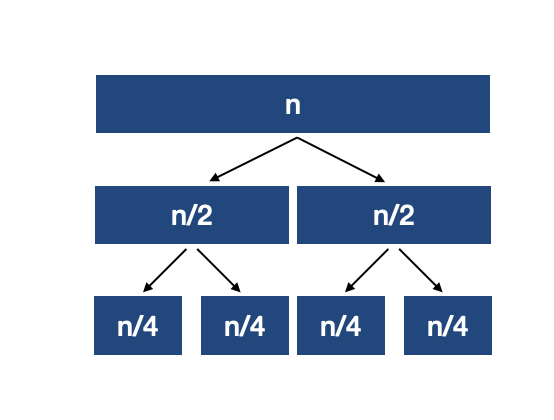
동작 과정

1) Divide

입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.

2) Conquer

부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면(left<right) 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.

3) Combine

정렬된 부분 배열들을 하나의 배열에 합병한다.

풀이 코드

mergeSort(left, right)

int l = left; 왼쪽 분할 문제 시작 인덱스
int r = mid+1; 오른쪽 분할 문제 시작 인덱스
int idx = l; l은 항상 mid+1보다 작기 때문에 분할 배열(tmp)의 저장 위치는 l(idx)로 지정

왼쪽 분할에서 값 가져오는 경우

r > right 오른쪽 분할의 원소를 이미 다 가져온 경우
l <= mid && arr[l] < arr[r] 왼쪽 분할에서 가져오지 않은 원소가 있고, 해당 원소 값(arr[l])이 오른쪽 분할의 원소 값(arr[r])보다 작은 경우

그 외의 경우에서는 오른쪽 분할에서 값을 가져온다. 그렇게 두 분할에서 모든 원소를 가져오면 left~right까지 새로운 값을 입력하여 저장해준다.

import java.io.*;

public class Main {
	
	static int[] arr, tmp;
	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();
		int n = Integer.parseInt(br.readLine());
		arr = new int[n];
		tmp = new int[n];
		for(int i=0; i<n; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}
		mergeSort(0, n-1);
		for(int num : arr) {
			sb.append(num+"\n");
		}
		System.out.println(sb.toString());
	}
	
	static void mergeSort(int left, int right) {
		if(left >= right) return;
		
		int mid = (left+right)/2;
		// divide
		mergeSort(left, mid); // 왼쪽 분할
		mergeSort(mid+1, right); // 오른쪽 분할
		
		// 분할(divide) -> 합병(merge)
		merge(left, mid, right);
	}
	
	static void merge(int left, int mid, int right) {
		int l = left;
		int r = mid+1;
		int idx = l;
		
		while(l <= mid || r <= right) {
			// 1. 오른쪽 분할의 원소를 이미 다 가져온 경우
			// 2. 왼쪽 분할에서 가져오지 않은 원소가 있고, 해당 원소(l)가 오른쪽 분할 원소(r)보다 작은 경우
			if(r>right || (l<=mid && arr[l]<arr[r])) {
				tmp[idx++] = arr[l++];
			}else { // 위에 해당하지않으면 오른쪽 분할에서 원소를 가져온다.
				tmp[idx++] = arr[r++];
			}
		}

		// left~right구간 정렬한 부분을 원래 배열 arr에 저장한다.
		for(int i=left; i<=right; i++) {
			arr[i] = tmp[i];
		}
	}

}

알고리즘	최대 실행 시간	최소 실행 시간	평균 실행 시간
병합 정렬	O(nlgn)	O(nlgn)	O(nlgn)

퀵 정렬

특정 원소 피봇(pivot)을 기준으로 주어진 배열을 두 부분 배열로 분할하고 각 부분 배열에 대해 퀵 정렬을 순환적으로 적용하는 방식이다.

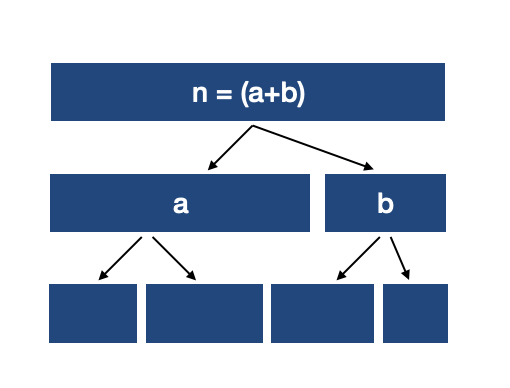
동작 과정

1) Divide

피봇 하나를 선택하여 피봇을 기준으로 2개의 부분 배열로 분할한다.

2) Conquer

피봇을 기준으로 피봇보다 큰 값, 혹은 작은 값을 찾는다. 왼쪽에서 부터 피봇보다 큰 값을 찾고 오른쪽에서 부터는 피봇보다 작은 값을 찾아서 두 원소를 교환한다. 분할된 부분 배열의 크기가 0이나 1일 될때까지 반복한다.

3) Combine

conquer과정에서 값의 위치가 바뀌므로 따로 결합은 하지 않는다.

📚 풀이 코드

int pivot = arr[left]; 왼쪽 피봇 선택 방식 사용 (상황에 따라 오른쪽, 중간 선택 방식을 사용할 수 도 있다)
while(i<j) 엇갈릴 때까지 반복한다.
- while(arr[j] > pivot && i<j) j--; 오른쪽에서부터 피봇 값보다 작은 값을 만날 때까지 탐색한다.
- while(arr[i] <= pivot && i<j) i++; 왼쪽에서부터 피봇 값보다 큰 값을 만날 때 까지 탐색한다.
- swap(i, j); i,j의 값을 찾았으면 위치를 바꿔준다.

swap(left, i); 맨 처음 pivot으로 설정했던 위치(arr[left]; 가장 큰 값)의 원소와 i가 가르키는 위치를 바꿔준다.

import java.io.*;

public class Main {
	
	static int[] arr;
	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();
		int n = Integer.parseInt(br.readLine());
		arr = new int[n];
		for(int i=0; i<n; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}
		quickSort(0,n-1);
		
		for(int num : arr) {
			sb.append(num+"\n");
		}
		System.out.println(sb.toString());
		
	}
	
	static void quickSort(int left, int right) {
		if(left>= right) {
			return;
		}
		
		int pivot = partition(left, right);
		quickSort(left,pivot-1);
		quickSort(pivot+1,right);
	}
	
	// 왼쪽 피봇 선택하는 경우
	static int partition(int left, int right) {
		int pivot = arr[left];
		int i = left;
		int j = right;
		while(i < j) {
			while(arr[j] > pivot&& i<j) {
				j--;
			}
			while(arr[i] <= pivot && i<j) {
				i++;
			}
			swap(i,j);
		}
		swap(left,i);
		return i;
	}
	
	static void swap(int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}

}

퀵 정렬의 경우 피봇의 위치나 배열의 상태에 따라 최악의 경우 O(n^2)이 나올 수도 있다.

예로, [1 2 3 4 5 6 7 8 9 10]와 같은 이미 정렬된 배열을 오름차순으로 퀵정렬을 하면 N개의 원소를 N번 순회하므로 N^2이라는 시간이 걸리게 된다. 그래서 무작정 분할정복 알고리즘인 합병,퀵 정렬을 사용하기보다는 그 문제의 특성을 찾고 그에 맞는 적절한 정렬 알고리즘을 선택하는 것이 중요하다.

알고리즘	최대 실행 시간	최소 실행 시간	평균 실행 시간
퀵 정렬	O(n^2)	O(nlgn)	O(nlgn)

합병, 퀵 정렬 실행과정 보는 사이트

이진 탐색

정렬된 데이터를 효과적으로 탐색할 수 있는 방법이다. (정렬된 데이터만 사용 가능; 참고로 정렬되지 않은 데이터 탐색은 파라메트릭 서치로 가능)

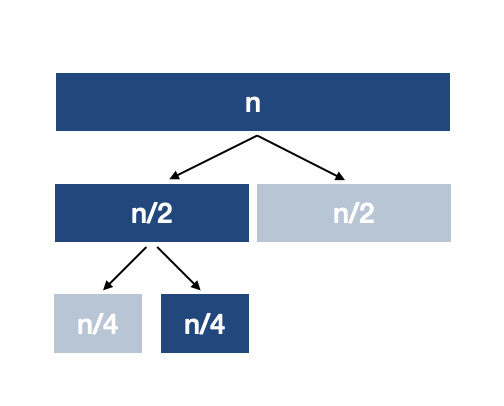
동작 과정

1) Divide

배열의 가운데 원소를 기준으로 왼쪽, 오른쪽 부분배열로 분할한다. 탐색키와 가운데 원소가 같으면 분할을 종료한다.

2) Conquer

탐색키가 가운데 원소보다 작으면 왼쪽 부분배열을 대상으로 이진 탐색을 순환 호출하고, 크면 오른쪽 부분배열을 대상으로 이진 탐색을 호출한다.

3) Combine

탐색 결과가 직접 반환되므로 결합이 불필요하다.

📚 풀이 코드

left : 배열 탐색 시작 인덱스, right : 배열 탐색 마지막 인덱스

// left : start, right: arr.length()-1
static int binarySearch(int[] arr, int left, int right, int key) {
	int mid =0;
	
	while(left<= right) {
		mid = (left+right)/2;
        
		if(key == arr[mid]) return mid;
        
		if(arr[mid] < key) {
			left = mid+1;
		}else {
			right = mid;
		}
	}
	return -1; // not found
}

☛ Arrays.binarySearch

 private static int binarySearch0(int[] a, int fromIndex, int toIndex,
                                     int key) {
        int low = fromIndex;
        int high = toIndex - 1;

        while (low <= high) {
            int mid = (low + high) >>> 1;
            int midVal = a[mid];

            if (midVal < key)
                low = mid + 1;
            else if (midVal > key)
                high = mid - 1;
            else
                return mid; // key found
        }
        return -(low + 1);  // key not found.
    }

이진탐색의 탐색 대상은 정렬이 되어 있어야하고 탐색대상 정렬 크기가 매 회 절반으로 줄어드므로, 시간 복잡도는 O(logn)을 가진다.

알고리즘	실행 시간
이진 탐색	O(nlgn)