[알고리즘] 단절점 (백준 11266번 풀이)

Dot Algo∙ DS/알고리즘 개념

[알고리즘] 단절점 (백준 11266번 풀이)

루지 2021. 12. 3. 13:36

#11266 단절점

난이도 : 플레 5

유형 : 그래프 이론 / 단절점 / DFS

11266번: 단절점

첫째 줄에 두 정수 V(1≤V≤10,000), E(1≤E≤100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B

www.acmicpc.net

▸ 문제

그래프가 주어졌을 때, 단절점을 모두 구해 출력하는 프로그램을 작성하시오. 단절점이란 그 정점을 제거했을 때, 그래프가 두 개 또는 그 이상으로 나누어지는 정점을 말한다. 즉, 제거했을 때 그래프의 connected component의 개수가 증가하는 정점을 말한다.

▸ 입력

첫째 줄에 두 정수 V(1≤V≤10,000), E(1≤E≤100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B가 주어진다. 이는 A번 정점과 B번 정점이 연결되어 있다는 의미이며, 방향은 양방향이다.

입력으로 주어지는 그래프는 연결 그래프가 아닐 수도 있다. 정점은 1부터 V까지 번호가 매겨져 있다.

▸ 출력

첫째 줄에 단절점의 개수를 출력한다.

둘째 줄에는 단절점의 번호를 공백으로 구분해 오름차순으로 출력한다.

문제 풀이

DFS로 풀 수 있는 응용 문제이다. 어떤 한 점과 인접한 간선을 모두 지웠을 때 해당 컴포넌트가 2개 이상으로 나뉘어지는 정점을 찾으면 된다. 풀이를 보기 전 미리 교차 간선이랑 역방향 간선에 대한 정의를 알아보고 가자.

교차 간선

스패닝 트리에서 선조와 자손관계가 아닌 정점들 간에 간선들을 의미한다. 무향(양방향) 그래프에는 존재하지 않는다.
간선 (u, v)가 교차 간선이기 위해서는 v가 먼저 방문된 후 u를 방문하지않고 종료되어야 하는데 양방향인 경우 v → u로 갈 수 있기 때문이다.

역방향 간선

스패닝 트리의 자손에서 선조로 연결되는 간선을 말한다.

한 정점(u)가 단절점인지 확인하기

DFS 탐색을 수행하면 다음과 같이 스패닝 트리를 만들 수 있다. 무향 그래프에서는 교차 간선이 없으므로, u와 연결된 정점은 선조아니면 자손이다.

이때 u의 자손들을 루트로 하는 서브트리들은 서로 연결되어 있지 않다. 그 간선들은 교차간선이어야 하는데 위에서 말했다시피 양방향 그래프에서는 교차 간선이 존재할 수 없기 때문이다. 따라서 그냥 하나의 서브트리로 구분된다.
따라서 u가 지워졌을 때 그래프가 쪼개지지 않는 유일한 경우는 그림과 같이 역방향 간선으로 연결되어 있을 때 뿐이라고 볼 수 있다.

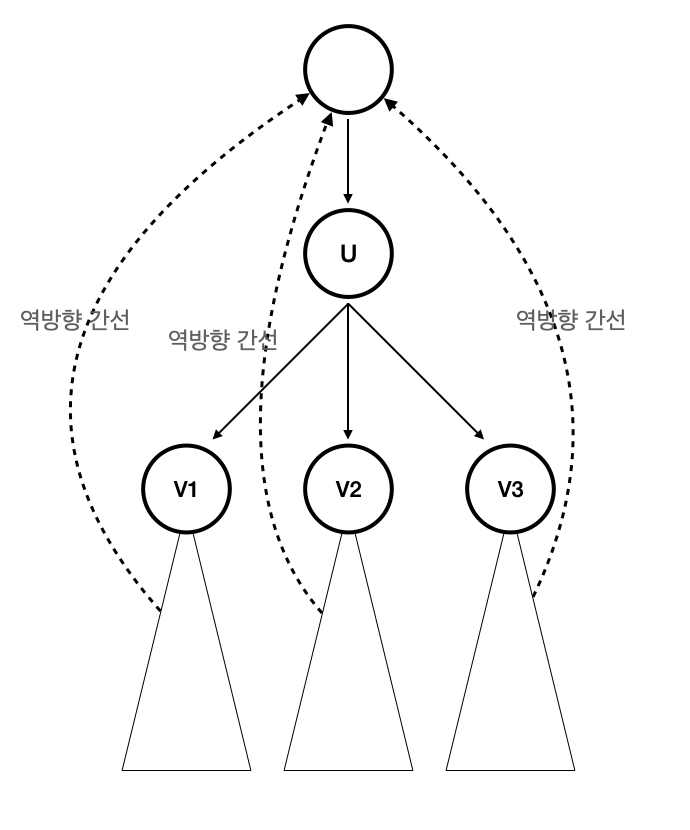
이를 확인할 수 있는 방법은 DFS를 수행하여 각 정점을 루트로 하는 서브트리에서 역방향 간선을 통해 갈 수 있는 정점의 최소 깊이를 반환하도록 하는 것이다. 만약 u의 자손들이 모두 역방향 간선을 통해 u의 선조로 올라갈 수 있다면 u는 단절점이 아니다.

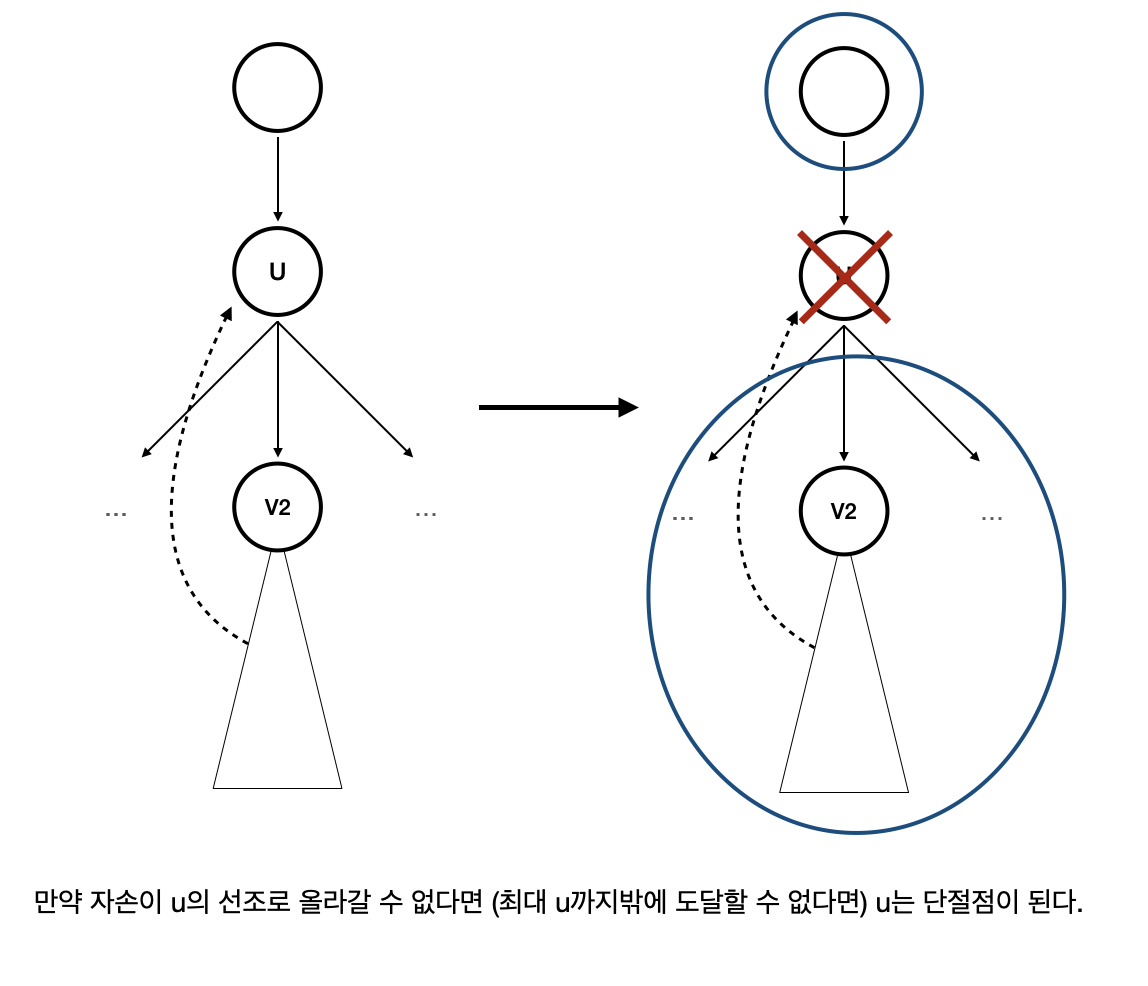
// 루트 노드가 아니고 subTree의 역방향 간선이 자기 자신 이하에 있다면 절단점
if(!isRoot && subTree >= discovered[cur]) { /
	isCutVertex[cur] = true;
}

u가 루트인 경우

u가 루트인 경우 예외는 자손이 하나 이하일 경우이다. 따라서, 둘 이상의 자손을 가질 때만 절단점이 된다.

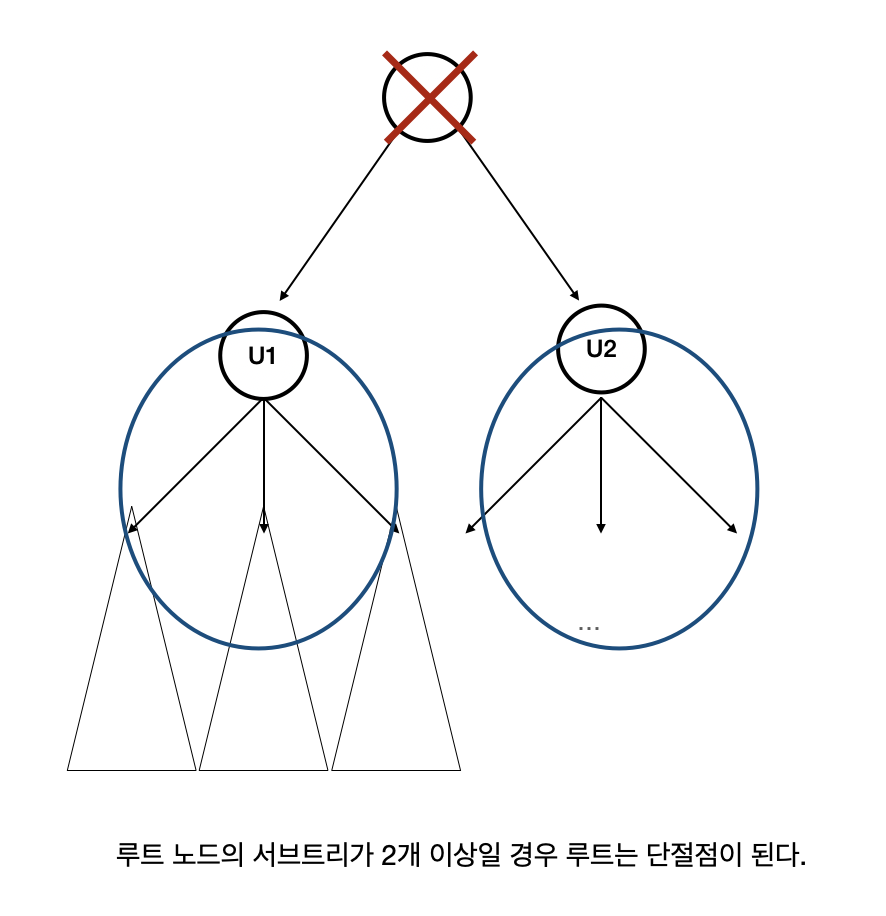
if(isRoot) {
	isCutVertex[cur] = child>=2;
}

해당 서브트리가 u의 조상 중 하나와 연결되어 있는지인데, u의 조상들은 u보다 먼저 발견되었을 것이다. 따라서 정점의 최소 깊이는 해당 정점을 루트로 하는 서브트리에서 역방향 간선을 통해 닿는 정점들의 가장 먼저 발견된 순서를 반환(discovered 최솟값)하도록 하면 된다.

설계

양방향 그래프 데이터를 입력받고, discovered 데이터를 -1로 초기화한다.
주어진 입력은 연결 그래프가 아니기 떄문에 모든 정점을 DFS 탐색한다. (discovered == -1인 경우)
findCutVertex(int cur, boolean isRoot)
1. 방문한 순서를 discovered[cur]에 저장해준다. discovered[cur] = counter++;
2. 해당 노드와 연결된 간선을 탐색한다. for(int i=0; i<list[cur].size(); i++)
3. 첫 방문일 경우 if(discovered[nxt] == -1)
  1. 연결된 간선(nxt)을 루트로 하는 서브트리에서 가장 먼저 발견된 정점번호를 반환한다. subTree
  2. 현재 노드(cur)가 루트가 아니고 subTree보다 먼저 발견된 정점이거나 자신이라면 해당 노드는 절단점이 된다.
  3. ret = 가장 먼저 발견된 정점의 값을 저장한다.
4. 이미 방문했을 경우
  1. ret = 가장 먼저 발견된 정점의 값을 저장한다.
5. root인 경우 if(isRoot)
  1. 서브 트리가 2개 이상이면 절단점이 된다.
6. ret를 반환한다. (해당 서브트리에서 역방향 간선으로 갈 수 있는 정점 중 가장 먼저 발견된 정점)
단절점의 갯수와 해당 노드번호를 출력해준다.

풀이 코드

import java.io.*;
import java.util.*;

public class Main {

	static List<Integer>[] list;
	static boolean[] isCutVertex;
	static int[] discovered;
	static int counter;
	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		int v = Integer.parseInt(st.nextToken());
		int e = Integer.parseInt(st.nextToken());
		
		isCutVertex = new boolean[v+1];
		discovered = new int[v+1];
		list = new ArrayList[v+1];
		for(int i=1; i<v+1; i++) {
			list[i] = new ArrayList<>();
			discovered[i] = -1;
		}
		
		for(int i=0; i<e; i++) {
			st = new StringTokenizer(br.readLine());
			
			int a = Integer.parseInt(st.nextToken());
			int b = Integer.parseInt(st.nextToken());
			
			list[a].add(b);
			list[b].add(a);
		}
		
		for(int i=1; i<v+1; i++) {
			if(discovered[i] == -1) {
				findCutVertex(i,true);	
			}
		}
		StringBuilder sb = new StringBuilder();
		int cnt = 0;
		for(int i=1; i<v+1; i++) {
			if(isCutVertex[i]) { 
				cnt++;
				sb.append(i+" ");
			}
		}
		System.out.println(cnt);
		if(cnt > 0) {
			System.out.println(sb.toString());	
		}
	}
	
	static int findCutVertex(int cur, boolean isRoot) {
		discovered[cur] = counter++;
		
		int ret = discovered[cur];
		int child =0;
		for(int i=0; i<list[cur].size(); i++) {
			int nxt = list[cur].get(i);
			if(discovered[nxt] == -1) {
				child++; // 루트 노드 subTree 카운트하기
				
				// 해당 서브트리에서 갈 수 있는 가장 먼저 발견된 정점 번호
				int subTree = findCutVertex(nxt, false);
				
				// 그 노드(subTree)가 자기 자신 이하에 있다면 절단점
				if(!isRoot && subTree >= discovered[cur]) {
					isCutVertex[cur] = true;
				}
				ret  = Math.min(ret, subTree); // 가장 먼저 발견된 정점 찾기
			}else {
				ret  = Math.min(ret, discovered[nxt]); // 가장 먼저 발견된 정점 찾기
			}
		}
		// 루트인 경우 서브트리가 2개 이상인 경우만 절단점
		if(isRoot) {
			isCutVertex[cur] = child>=2;
		}
        
		// 해당 서브트리에서 가장 먼저 발견된 정점(discovered) 반환
		return ret;
	}
}