[자료구조] 힙(Heap) 구현하기 - 우선순위 큐 (Java)

Dot Algo∙ DS/자료구조

[자료구조] 힙(Heap) 구현하기 - 우선순위 큐 (Java)

루지 2022. 1. 5. 00:00

우선순위 큐

우선순위 큐는 일반 큐와는 달리 우선순위가 가장 높은 자료가 가장 먼저 꺼내지는 자료구조이다.

수행할 작업이 여러 개 있고 시간이 제한되어 있을 때 우선순위가 높은 것부터 수행한다거나 하는 일이 자주있기 때문에 우선순위 큐 자료구조는 자주 쓰인다.
그 사용 예로, 시뮬레이션 시스템. 네트워크 제어, 작업 스케쥴링 등이 있다.

우선순위 큐를 구현하는 방법은 여러가지가 있다.

연결리스트, 배열
균형잡힌 이진 검색 트리
힙

먼저 간단하게 연결 리스트나 배열로 구현하면 해당 자료구조에 원소를 모두 집어넣고, 원소를 꺼낼 때 마다 모든 원소를 순회하며 우선순위가 높은 원소를 찾는 방식을 사용해야 하는데, 이러면 원소 추가 O(1), 검색 O(n)이 걸린다.

균형잡힌 이진 검색 트리로 구현하는 것은 소 잡는 칼로 닭을 잡는 격으로, 구현이 까다롭다. 원소들을 우선순위로 정렬해 두면 최대 원소를 찾아 삭제하는 일과 새 원소를 삽입하는 일 모두 O(logN) 시간에 할 수 있다.

가장 효율적인 방법은 바로 힙(Heap)으로 구현하는 것이다. 이진 검색 트리보다 훨씬 간단한 구조로 구현할 수 있고, 최적화된 형태의 이진 트리로, 힙을 사용하면 새 원소를 추가하는 연산과 가장 큰 원소를 꺼내는 연산 모두 O(logN) 시간에 할 수 있다.

	연결리스트, 배열	균형잡힌 이진 검색 트리(BST)	힙(Heap)
구현	구현 쉬움	구현 어려움	구현 쉬움
원소 추가	O(1)	O(logN)	O(logN)
원소 삭제	O(n)	O(logN)	O(logN)

힙 정의 및 구현

힙은 특정한 규칙을 만족하도록 구성된 이진 트리로, 단순히 최대 원소를 가능한 한 빠르게 찾을 수 있는 방법으로 설계되었기 떄문에 더 단순한 알고리즘으로도 효율적으로 동작할 수 있다.

대소 관계 규칙

힙의 가장 중요한 규칙은 부모 노드가 가진 원소는 항상 자식 노드가 가진 원소 이상이라는 것이다. 이를 힙의 대소 관계 규칙이라고 한다.

이진 검색 트리와는 달리 부모 자식 관계에만 적용되며, 왼쪽 자식과 오른쪽 자식이 갖는 원소의 크기는 제한하지 않는다.
이 규칙에 의하면 트리에서 가장 큰 원소는 항상 트리의 루트에 들어가므로, 최대 원소를 빨리 찾기를 원하는 힙의 목적에 잘 부합한다.

트리 높이 항상 일정하게 유지

이진 검색 트리에서도 문제가 되었던 편향 트리가 나오지 않게하기 위해서 힙은 트리의 높이를 항상 일정하게 유지하기 위해 트리의 구조에 제약을 둔다.

이것은 균형 잡힌 이진 검색 트리가 트리의 구조를 제약해 속도를 더 빠르게 하는 것과 같다.

힙의 모양 규칙

힙의 모양 규칙은 다음과 같은 두 가지 조건으로 이루어진다.

마지막 레벨을 제외한 모든 레벨에 노드가 꽉 차있어야 한다.
마지막 레벨에 노드가 있을 때는 항상 가장 왼쪽부터 채워져 있어야 한다.

이 두 가지의 모양 규칙을 모두 만족한다면, 트리에 포함된 노드의 개수만으로 트리의 모양이 정해진다. 예를 들어일곱 개의 원소가 들어 있는 모든 힙은 다음과 같은 상태를 가질 수 밖에 없다.

또한 이 규칙을 만족할 때 트리의 높이는 항상 logN이라는 사실도 쉽게 알 수 있다.

힙의 모양 규칙은 BST보다 훨씬 엄격하다. 이처럼 엄격한 조건을 내세울 수 있는 이유는 힙이 요구하는 대소 관계 조건이 BST가 요구하는 조건(중위 검색 결과가 정렬되어 있을 것)보다 훨씬 느슨하기 때문이다.

힙 구현

엄격한 규칙은 구현할 때 장점으로 작용한다. 트리의 포함된 노드의 개수만 알면 트리 전체 구조를 알 수 있기 때문이다. 그래서 대부분의 힙 구현은 이 점을 최대한 이용해 배열 하나로 전체 트리를 표현한다.

힙의 모양 규칙에 의해, n개의 노드가 있을 떄 이 노드들은 arr[0]에서 arr[n-1]까지 순차적으로 대응된다.

arr[i]의 왼쪽 자식은 arr[2*i + 1]에 대응된다.
arr[i]의 오른쪽 자식은 arr[2*i]에 대응된다.
arr[i]의 부모는 arr[(i-1)/2]에 대응된다. (나눗셈 결과는 내림한다.)

힙 삽입(새 원소 추가)

새 원소를 추가할 때는 대소 관계 규칙 대신 모양 규칙을 먼저 만족시켜줘야 한다.

이진 검색 트리는 대소 관계 규칙에 따라 정해지지만 힙은 모양 규칙에 따라 정해진다. 트리의 크기가 증가했을 떄 새로 생겨나야 할 노드의 위치가 모양 규칙에 의해 결정되기 때문이다.
모양 규칙에 의해 항상 heap[]의 맨 끝에 추가된다.

모양 규칙을 만족시켰으면 이젠 대소 관계를 만족시켜주면 된다.

마지막에 추가한 새 원소를 자신의 부모 노드가 가진 원소와 비교하고, 부모 노드가 가진 원소가 작다면 두 원소의 위치를 바꾼다.
새 원소가 더 크거나 같은 원소를 가진 부모 노드를 만나거나, 루트에 도달할 때 까지 반복한다.

다음과 같이 구현 할 수 있다. 시간 복잡도는 트리의 높이인 O(logN)이다.

public void push(int val){
	heap.add(val);
	int idx =  heap.size()-1;

	// 루트에 도달하거나 새 원소 이상의 원소를 가진 조상을 만날 때 까지
	// idx 0부터 시작하므로 idx-1
	while(idx > 0 && heap.get((idx-1)/2) < heap.get(idx)){
		swap((idx-1)/2, idx, heap.get((idx-1)/2), heap.get(idx));
		idx = (idx-1)/2; // 부모로 이동
	}
}

private void swap(int to, int from, int a, int b) {
	int tmp = a;
	heap.set(to,  b);
	heap.set(from,  tmp);
}

힙 삭제(최대 원소 꺼내기)

최대 원소를 찾는 것은 간단한데 문제는 최대 원소를 힙에서 꺼내는 일이다. 엄격한 모양 제한 때문에 이진 검색 트리처럼 구현하기는 까다롭다. 그래서 이번에도 모양 규칙을 먼저 고려해줘야 한다.

어차피 마지막 노드는 지워질 운명이기 때문에, 이 노드를 일단 지우고 시작한다. 이 노드는 리프이기 떄문에 노드가 지워진다고 해도 힙의 구조에 끼치는 영향은 없다.
그리고 이 마지막 노드에 있던 원소를 루트에 옮겨준다.

이제 대소 관계를 만족시키기만 하면 된다.

힙의 대소 관계를 만족시키려면 원래 루트의 두 자식이 가지고 있던 원소 중 큰 쪽이 루트에 올라온다.
이 작업을 트리의 바닥에 도달하거나, 두 자손이 모두 자기 자신 이하의 원소를 갖고 있을 때까지 반복한다.

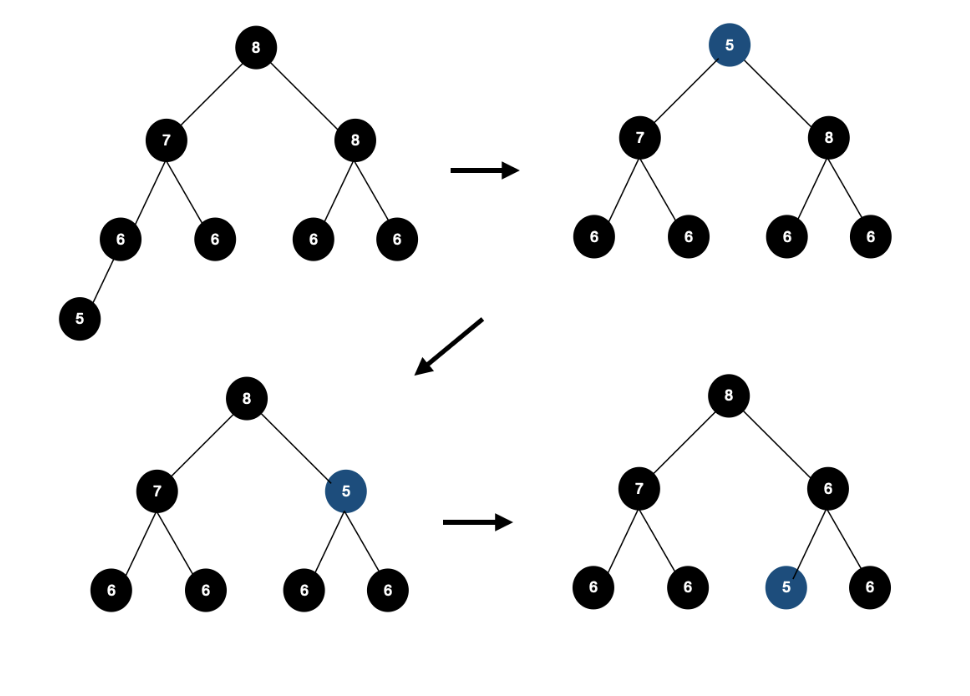
while문의 내부가 한 번 실행될 때마다 트리의 아래 레벨로 내려가기 때문에, 시간 복잡도는 O(logN)이 된다.

public int pop(){
	if(heap.isEmpty()) return 0;

	int delete = heap.get(0);
	heap.set(0, heap.get(heap.size()-1));
	heap.remove(heap.size()-1);

	int here = 0;
	while(true){
		int left = here * 2 + 1,  right = here * 2 + 2;

		// 리프에 도달한 경우
		if(left >= heap.size()) break;

		// heap[here]이 내려갈 위치를 찾는다.
		int next = here;

		// here vs 왼쪽 자식 노드
		if(heap.get(next) < heap.get(left)){
			next = left;
		}

		// 위 결과 vs 오른쪽 자식 노드
		if(right < heap.size() && heap.get(next) < heap.get(right)){
			next = right;
		}

		if(next == here) break;

		swap(here, next, heap.get(here), heap.get(next));
		here = next;
	}

	return delete;

}

private void swap(int to, int from, int a, int b) {
	int tmp = a;
	heap.set(to,  b);
	heap.set(from,  tmp);
}

MaxHeap 구현 코드

전체 구현 코드는 다음과 같다.

public class MaxHeap {

   private List<Integer> heap;

   public MaxHeap() {
      heap = new ArrayList<>();
   }

   // 정수를 담는 최대 힙에 새 원소 삽입
   public void push(int val){
      heap.add(val);
      int idx =  heap.size()-1;

      // 루트에 도달하거나 새 원소 이상의 원소를 가진 조상을 만날 때 까지
      // idx 0부터 시작하므로 idx-1
      while(idx > 0 && heap.get((idx-1)/2) < heap.get(idx)){
         swap((idx-1)/2, idx, heap.get((idx-1)/2), heap.get(idx));
         idx = (idx-1)/2; // 부모로 이동
      }
   }

   private void swap(int to, int from, int a, int b) {
      int tmp = a;
      heap.set(to,  b);
      heap.set(from,  tmp);
   }

   public int pop(){
      if(heap.isEmpty()) return 0;

      int delete = heap.get(0);
      heap.set(0, heap.get(heap.size()-1));
      heap.remove(heap.size()-1);

      int here = 0;
      while(true){
         int left = here * 2 + 1,  right = here * 2 + 2;

         // 리프에 도달한 경우
         if(left >= heap.size()) break;

         // heap[here]이 내려갈 위치를 찾는다.
         int next = here;

         // here vs 왼쪽 자식 노드
         if(heap.get(next) < heap.get(left)){
            next = left;
         }

         // 위 결과 vs 오른쪽 자식 노드
         if(right < heap.size() && heap.get(next) < heap.get(right)){
            next = right;
         }

         if(next == here) break;

         swap(here, next, heap.get(here), heap.get(next));
         here = next;
      }

      return delete;

   }

   public static void main(String[] args) {
      MaxHeap heap = new MaxHeap();
      Random random = new Random();

      for(int i=0; i<100; i++){
         heap.push(random.nextInt(100));
      }

      System.out.println(heap);

      for(int i=0; i<100; i++){
         System.out.println(heap.pop());
      }
   }
}