[알고리즘] 외판원 순회 문제(TSP: Travelling Salesman Problem) 정리 (Java)
외판원 순회 문제 (TSP: Travelling Salesman Problem)
TSP(Travelling Salesman Problem, 일명 ‘여행하는 외판원 문제’)는 조합 최적화(Combinatorial Optimization) 문제로 전산학에서 연구된 가장 유명한 문제 중 하나다.

여러 도시들이 있고 한 도시에서 다른 도시로 이동하는 비용이 모두 주어졌을 때, 모든 도시들을 단 한 번만 방문하고 원래 시작점으로 돌아오는 최소 비용의 이동 순서를 구하는 것이다. 그래프 이론의 용어로 엄밀하게 정의한다면, "각 변에 가중치가 주어진 완전 그래프(weighted complete graph)에서 가장 작은 가중치를 가지는 해밀턴 순환을 구하라"라고 표현할 수 있다. 즉 해밀턴 순환에 저비용 조건만 추가해주면 된다. 이 문제는 반드시 시작점으로 돌아와야 한다는 제약 조건을 없애도 계산 복잡도는 변하지 않는다.
외판원 순회 알고리즘은 무식하게 풀 수 있다. 무조건 0번 도시에서 출발한다고 가정해도 경로의 길이는 다르지 않다. 그러면 남은 도시들을 어떤 순서로 방문할지를 정하기만 하면 된다. 남은 n-1개의 도시를 나열하는 방법으로는 (n-1)!가지가 있다. 그래서 재귀 호출을 통해 쉽게 외판원 순회 알고리즘을 설계할 수 있다. 그러나 보통 n!의 풀이는 사용하지 않는다. 12!만 해도 479,001,600라는 엄청난 수를 지니기 때문이다.
외판원 순회 알고리즘을 더 빠르게 구할 수는 없을까?
모든 정점을 한 번씩 방문하는(출발 정점 제외) 최단 순환 경로를 탐색하는데 이는 최적의 효율로 탐색하기 위해서이다. 정점 N의 최대크기는 16라고 해보자. 위에서 말했다시피 만약 완전탐색으로 모든 경로를 조회하면서 답을 구하려고 한다면 첫 번째 지점을 제외하고 탐색하여도 (16-1)! = 약 1.3조 정도가 되어 시간초과가 발생할 것이다. 게다가 모든 경로의 상태를 저장하는 n개의 상태를 저장하는 배열 크기도 필요하다.
DP 메모제이션
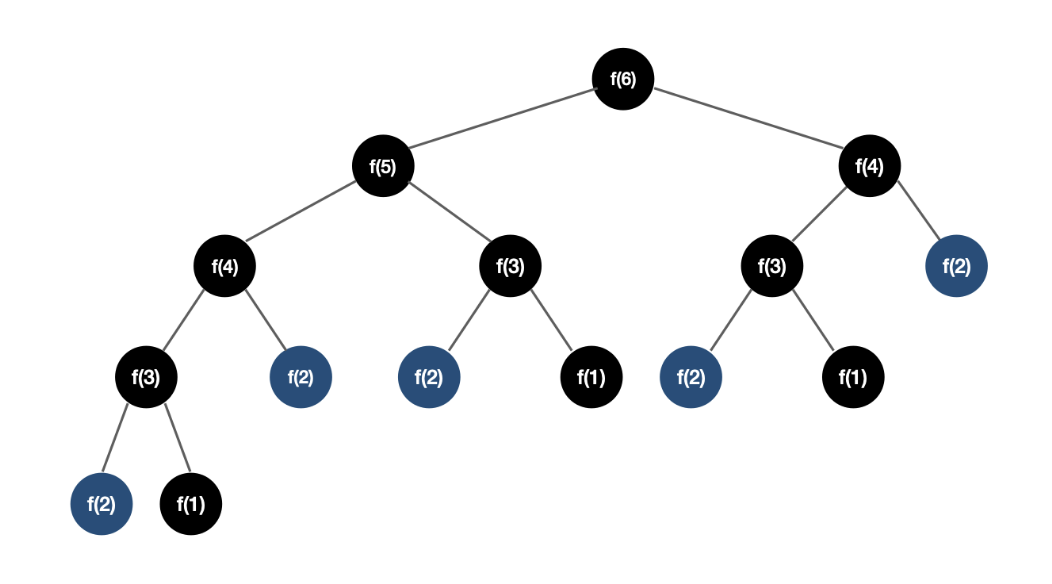
(16-1)!의 모든 경로를 조사하지 않고 중복된 경로를 제거하는 dp 메모제이션기법을 사용하면 된다. 동일한 하위 문제의 반복을 막아줌으로써 더 높은 효율로 연산이 이루어지게 해준다. 중복되는 경로의 조사를 제거해주는 것이다.
- 예를 들면, 피보나치 함수는 dp메모제이션 기법을 통해 O(2^n)의 복잡도를 O(n)까지도 줄여준다. 그렇다고 무조건 dp 메모제이션을 적용하면 O(n)으로 줄어든다는 뜻은 아니다. 각 문제 성질마다 다르다.
비트마스킹
이는 알고리즘 풀이할 때 종종 사용하는 공간 최적화 기법이다. 비트마스킹을 사용하면 bit연산이기 때문에 다른 자료구조(boolean배열)을 사용하는 것보다 훨씬 빠르게 동작되고 코드도 간결해진다. 그리고 가장 큰 장점은 N이 16개인 경우 2^16가지의 경우를 16bit로 표현이 가능하다. (ex. 16개의 지점 중 1,3,4,5번 지점 방문 -> 0000 0000 0001 1101)
→ 정리하면 TSP(외판원 순회)는 최단 순환 경로를 탐색해야하는데 1) N! 의 중복 경로를 제거해주는 DP 메모제이션 기법을 사용한다. 그래도 2^N의 모든 경우의 수를 표현해야 하기 때문에 그만큼의 공간복잡도가 필요하다. 2) 메모리 사용량도 줄이고 성능 향상을 위해서 2^N의 경우의 수를 Nbit로 표현할 수 있는 비트마스킹으로 사용한다.
왜 한 정점만 탐색해도 될까?
DP 메모제이션 기법으로 엄청나게 시간을 단축 할 수 있는 것은 그만큼 중복되는 경로가 많기 때문이다. TSP는 한 정점에서 다른 모든 정점을 순회하여 다시 출발 정점으로 돌아오는 최적의 경로를 찾는 알고리즘이다. 이 순회 경로는 싸이클로 n개의 정점 중 어느 정점에서 탐색을 시작을 해도 결과는 똑같다는 것을 알아야한다.
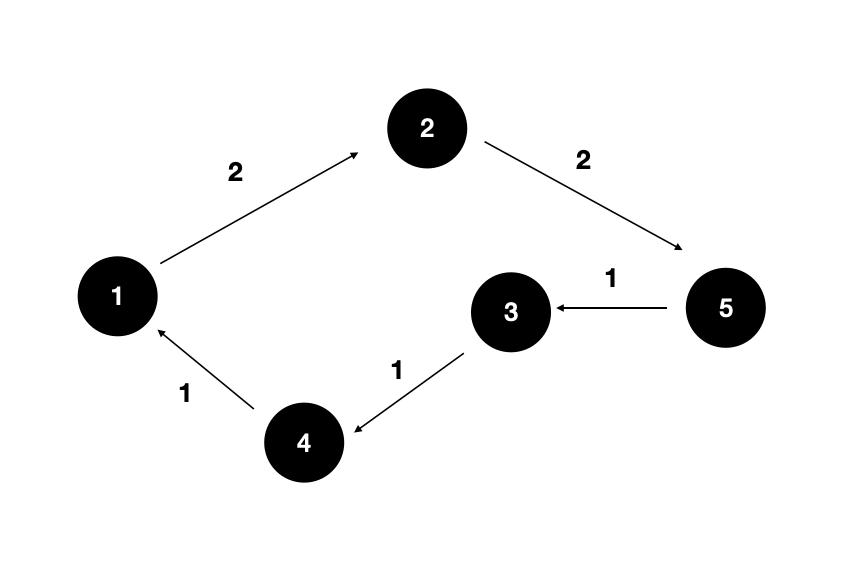
어차피 최적 경로 싸이클은 어디서 시작해도 다 똑같이 나온다. 그래서 한 정점에서만 탐색해줘도 된다.
- 1번에서 출발 : 1 → 2 → 5 → 3 → 4 → 1
- 2번에서 출발 : 2 → 5 → 3 → 4 → 1 → 2
- 3번에서 출발 : 3 → 4 → 1 → 2 → 5 → 3
외판원 순회 문제 풀어보기