[알고리즘] 최적화 문제 결정 문제로 바꿔풀기 - 파라메트릭 서치(Parametric Search)
최적화 문제 결정 문제로 바꿔풀기
딱히 이름이 붙어 있지 않지만 굉장히 유용한 디자인 원칙 중 하나로, 최적화 문제를 결정 문제(decision problem)으로 바꾼 뒤, 이것을 이분법(이진 탐색과 비슷하게 수치 해석 문제를 해결하는 기법)을 이용해 해결하는 방법이다. 결정 문제란 예 혹은 아니오 형태의 답만이 나오는 문제들을 가리킨다.
- 최적화 문제의 반환 값은 대개 실수나 정수이므로 답의 경우의 수가 무한한 데 반해,
- 결정 문제는 두 가지 답만이 있을 수 있다.
다음은 여행하는 외판원 문제(TSP)를 최적화 문제와 결정 문제로 표현한 것이다.
- optimize(G) = 그래프 G의 모든 정점을 한 번씩 방문하고 시작점으로 돌아오는 최단 경로의 길이를 반환한다. (최적화 문제)
- decision(G, x) = 그래프 G의 모든 정점을 한 번씩 방문하고 시작점으로 돌아오면서 길이가 x 이하인 경로의 존재 여부를 반환한다. (결정 문제)
optimze()는 가장 짧은 경로의 길이를 실수로 반환하지만, decision()은 최단 경로건 아니건 간에 x보다 짧은 경로가 있는지만 확인하면 된다.
최적화 문제와 결정 문제의 관계
같은 문제를 최적화 문제 형태와 결정 문제 형태로 만들었을 때, 푸는 데 시간이 더 오래 걸리는 쪽은 어느 쪽일까? 이 질문에 대한 답은 둘 중에 하나이다.
- 두 문제 형태가 똑같이 어려운 경우
- 최적화 문제가 더 어려운 경우
결정문제 난이도 ≤ 최적화문제 난이도
다시 말해 결정 문제가 최적화 문제보다 어려울 수는 없다는 뜻이다. 왜냐하면 최적화 문제를 푸는 optimize()가 있으면 결정 문제는 다음과 같이 한 줄로 짤 수 있기 때문이다.
double optimize(List<Integer>[] list){
// ...
// ...
// ...
}
boolean decision(List<Integer>[] list, double x){
return optimize(list) <= x;
}
파라메트릭 서치 (Parametric Search)
대표적으로 최적화 문제 결정 문제로 바꿔풀기 예시로는 코테에 종종 등장하는 '파라메트릭 서치'가 있다. 이진탐색과 유사하지만 파라메트릭 서치는 최적화 문제를 결정 문제로 바꾸어 푸는 데 사용된다.
| 이진탐색 | 파라메트릭 서치 | |
| 정의 | 정렬된 일련의 값들이 주어졌을 때 그 값들 중 원하는 값을 찾는 알고리즘 | 주어진 범위 내에서 원하는 값 또는 조건에 일치하는 값을 찾아내는 알고리즘 |
| 예시 | 1부터 9까지의 정렬된 배열에서 3이라는 값을 찾는다. | 1~9범위 내에서 3이라는 값 또는 원하는 조건에 일치하는 값을 찾아가는 것 |
파라메트릭 서치 문제
카카오 인턴 기출 5번 시험장 나누기 문제를 간단하게 파라메트릭 서치 풀이 부분만 예로 들어보자.
코딩테스트 연습 - 시험장 나누기
3 [12, 30, 1, 8, 8, 6, 20, 7, 5, 10, 4, 1] [[-1, -1], [-1, -1], [-1, -1], [-1, -1], [8, 5], [2, 10], [3, 0], [6, 1], [11, -1], [7, 4], [-1, -1], [-1, -1]] 40
programmers.co.kr
코딩 테스트를 총괄하는 무지는 안정적인 시험을 위해, 시험장에서 오는 트래픽을 k개의 그룹으로 나누어 각 그룹별 서버로 분산시키기로 하였습니다. 시험장 사이를 연결한 간선들 중 k-1개를 끊어서 시험장을 k 개의 그룹으로 나눌 계획입니다. 이때, 그룹별 최대 트래픽을 최소화하기 위하여 가장 큰 그룹의 인원을 최소화시켜야 합니다.

파라메트릭 서치 풀이
트리를 k개 이하의 그룹으로 나누어서 얻을 수 있는 최소한의 최대 그룹의 크기를 구하는 최적화 문제가 주어졌을 때 다음과 같이 풀 수 있다.
- 주어진 최적화 문제: “트리를 k개 이하의 그룹으로 나누어서 얻을 수 있는 최소한의 최대 그룹의 크기는 얼마인가?”
- 변경된 결정 문제: “트리를 k개 이하의 그룹으로 나누어서 얻을 수 있는 최대 그룹의 크기가 L 이하가 되도록 할 수 있는가?”
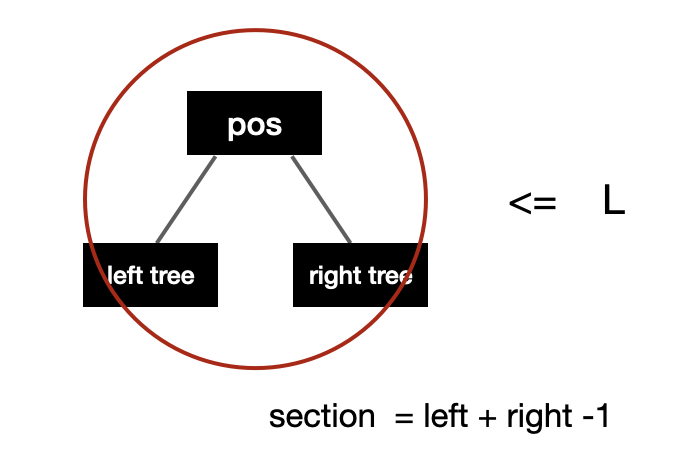
트리를 k개 그룹을 나누었을 때, 최대 그룹의 가중치 합(L)이 (전체 가중치 합)/k보다는 작을 수 없기 때문에 L의 범위는 다음과 같다.
- (전체 가중치 합) / k ≤ L ≤ (전체 가중치 합)
1번의 예제로 예시를 들면 (전체 가중치 합) = 112이고, k=3이다.
아무리 최대 그룹의 가중치 합을 최소로 만들려고 노드의 데이터를 구성해봐도 112/3 = (int)38이 최소이다.
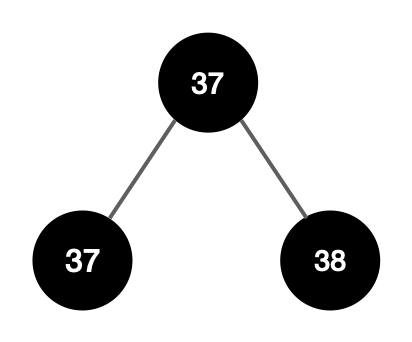
해당 범위내에서 파라메트릭 서치를 해주면 된다.
int left = sum/k;
int right = sum;
while(left+1 < right) {
int mid = (left+right)/2;
cost = new int[size][2];
traversal(root, mid);
if(cost[root][0] <= k) {
right = mid;
}else {
left = mid;
}
}
파라메트릭 서치 문제 풀어보기
참고