#10451 순열 사이클
난이도 : 실버 1
유형 : 그래프 탐색(DFS)/ 순열 사이클 또는 Union-find
10451번: 순열 사이클
1부터 N까지 정수 N개로 이루어진 순열을 나타내는 방법은 여러 가지가 있다. 예를 들어, 8개의 수로 이루어진 순열 (3, 2, 7, 8, 1, 4, 5, 6)을 배열을 이용해 표현하면 \(\begin{pmatrix} 1 & 2 &3&4&5&6&7&8 \ 3
www.acmicpc.net
▸ 문제
1부터 N까지 정수 N개로 이루어진 순열을 나타내는 방법은 여러 가지가 있다. 예를 들어, 8개의 수로 이루어진 순열 (3, 2, 7, 8, 1, 4, 5, 6)을 배열
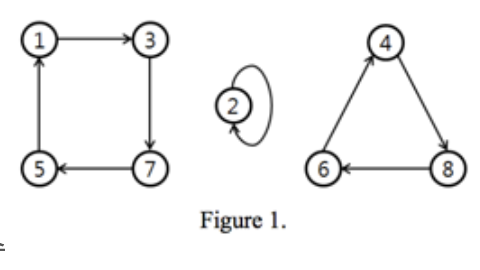
을 이용해 표현하면 (1234567832781456) 와 같다. 또는, Figure 1과 같이 방향 그래프로 나타낼 수도 있다.
순열을 배열을 이용해 (1…i…nπ1…πi…πn) 로 나타냈다면, i에서 πi로 간선을 이어 그래프로 만들 수 있다.
Figure 1에 나와있는 것 처럼, 순열 그래프 (3, 2, 7, 8, 1, 4, 5, 6) 에는 총 3개의 사이클이 있다. 이러한 사이클을 "순열 사이클" 이라고 한다.
N개의 정수로 이루어진 순열이 주어졌을 때, 순열 사이클의 개수를 구하는 프로그램을 작성하시오.
▸ 입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 순열의 크기 N (2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 순열이 주어지며, 각 정수는 공백으로 구분되어 있다.
▸ 출력
각 테스트 케이스마다, 입력으로 주어진 순열에 존재하는 순열 사이클의 개수를 출력한다.
문제 풀이
처음에 싸이클 찾으래서 잘 안 사용하는 서로소집합 알고리즘 Union-find을 연습할겸 사용했다. 그런데 이상하게 예제는 다 풀리는데 9%에서 막혀서 풀이를 바꿨다. DFS탐색으로는 가볍게 풀리는 문제이다.
그리고 아래에 Union-find의 풀이도 추가하였다. (해결법 찾음!)
조건
1) 순열 크기 N : 2<= N <=1,000
2) 1부터 N까지 정수 N개로 이루어진 순열
순열 싸이클의 개수를 구하는 문제이므로 당연히 인접탐색 BFS보다는 내가 좋아하는 깊이탐색 DFS를 사용했다.
*유의할 점은 방문여부를 전역으로 잘 체크해줘야한다.
풀이 코드
import java.io.*;
import java.util.*;
public class Main {
static int[] map;
static boolean[] check;
static int cycle;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = null;
int t = Integer.parseInt(br.readLine());
for(int test=0; test<t; test++) {
int n = Integer.parseInt(br.readLine());
map = new int[n+1];
cycle=0;
st = new StringTokenizer(br.readLine());
for(int i=1; i<n+1; i++) {
map[i] = Integer.parseInt(st.nextToken());
}
check = new boolean[n+1];
for(int i=1; i<n+1; i++) {
if(!check[i]) {
dfs(i);
cycle++;
}
}
System.out.println(cycle);
}
}
static void dfs(int start) {
check[start]= true;
int next= map[start];
if(!check[next]) {
dfs(map[start]);
}
}
}
Union-find 풀이
처음에 안풀린 풀이과정 더보기 클릭
처음에는 union-set배열에서 ranks를 추가하여 풀이를 해보았다.
∙ parents 배열 : i의 부모노드를 저장
∙ ranks 배열 : i를 부모로 삼는 자식노드의 수를 저장
예시
1
1
3 4 2 1
만약 위의 예제를 실행한다면 풀이는 아래와 같이 진행됩니다.
| node | Parents (x,y) | 1 | 2 | 3 | 4 | Ranks (x,y) | 1 | 2 | 3 | 4 |
| 1 -> 3 | x = 1, y = 3 | 1 | 2 | 1 | 4 | ranks[1] = 0 ranks[3] = 0 |
1 | 0 | 0 | 0 |
| 2 -> 4 | x = 2, y = 4 | 1 | 2 | 1 | 2 | ranks[2] = 0 ranks[4] = 0 |
1 | 1 | 0 | 0 |
| 3 -> 2 | x = 1, y = 2 | 1 | 1 | 1 | 2 | ranks[1] = 1 ranks[2] = 1 |
3 | 0 | 0 | 0 |
| 4 -> 1 | x = 1, y = 1 | 1 | 1 | 1 | 2 | ranks[1] = 2 ranks[1] = 2 |
4 | 0 | 0 | 0 |
* 3->2 일 때는 자식이 1이상인 부모노드가 만나 두 개의 싸이클에서 하나로 합쳐져 ranks[2]를 감소시키고 ranks[1]을 증가시켰습니다.
실패한 풀이 ✔︎
import java.io.*;
import java.util.*;
public class Main {
static int[] parents;
static int[] ranks;
static int cycle;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = null;
StringBuilder sb = new StringBuilder();
int t = Integer.parseInt(br.readLine());
for(int test=0; test<t; test++) {
int n = Integer.parseInt(br.readLine());
// --------------초기화--------------------
parents = new int[n+1];
ranks = new int[n+1];
cycle=0;
for(int i=1; i<n+1; i++) {
parents[i] = i;
}
st = new StringTokenizer(br.readLine());
// -------------- union-set --------------
for(int i=1; i<n+1; i++) {
int a = i;
int b = Integer.parseInt(st.nextToken());
union(a,b);
}
// -------------- 싸이클 찾기 --------------
for(int k=1; k<n+1; k++) {
if(ranks[k]!=0) {
cycle++;
}
}
sb.append(cycle+"\n");
}
System.out.println(sb.toString());
}
static int find(int x) {
if(parents[x] == x) return x;
int parent= find(parents[x]);
return parent;
}
static void union(int x, int y) {
x = find(x);
y = find(y);
// y가 부모
if(ranks[x] < ranks[y]) {
parents[x]= y;
ranks[y]++; // 자식 추가
}else {
parents[y] = x;
if(ranks[x]==ranks[y]) {
ranks[x]++; // 자식 추가
// 길이가 1이상인 두 싸이클이 하나로 합쳐질 때 (x부모, y자식)
if(ranks[y]!=0 && x!=y) {
ranks[x]++;
ranks[y]--;
}
}
}
}
}
위의 시행착오를 겪고 다시 단순히 생각해보았다. ranks의 배열은 싸이클을 판별하기에는 문제가 있는 것은 아닐까? 만약 수열의 한 조합이 꼬리가 있지만 싸이클이 되지 않는 경우(1->2->3)에는 ranks의 값은 2이지만 싸이클로 판별될 것이다. 이렇게 반례를 찾았다. 그렇다면 싸이클이 생성될 때만 카운트하면 되는데 이는 사실 Union-find만으로 쉽게 알아낼 수 있었다. 위상정렬 없이 그냥 Union-find로만 해결했다. union로직에서 x와 y가 일치하는 순간이 싸이클이 발생하는 순간이다.
예제로 과정을 보면 다음과 같다.
주어진 순열 그래프 (3 2 7 8 1 4 5 6)
i) 1 → 3 , x=1 y=3
☛ parents[3] =1
ii) 3 → 7 , x= find(3)= 1, y=7
☛ parents[7] =1
iii) 7 → 5 , x= find(7) = 1, y=5
☛ parents[5] =1
iv) 5 → 1 , x= find(5) = 1, y=1
x==y, 싸이클 생성!
위와 같은 방식으로 싸이클을 count하여 출력해주면 된다.
import java.io.*;
import java.util.*;
public class Main {
static int[] parents;
static int cycle;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = null;
StringBuilder sb = new StringBuilder();
int t = Integer.parseInt(br.readLine());
for(int test=0; test<t; test++) {
int n = Integer.parseInt(br.readLine());
parents = new int[n+1];
cycle=0;
for(int i=1; i<n+1; i++) {
parents[i] = i;
}
st = new StringTokenizer(br.readLine());
for(int i=1; i<n+1; i++) {
int a = i;
int b = Integer.parseInt(st.nextToken());
union(a,b);
}
sb.append(cycle+"\n");
}
System.out.println(sb.toString());
}
static int find(int x) {
if(parents[x] == x) return x;
int parent= find(parents[x]);
return parent;
}
static void union(int x, int y) {
x = find(x);
y = find(y);
if(x==y) {
cycle++; // 싸이클 생성
}
else if(x>y) {
parents[x]= y;
}else {
parents[y] = x;
}
}
}
'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 11062번 카드 게임 (Java) (0) | 2021.05.20 |
|---|---|
| [BOJ] 백준 1238번 파티 (Java) (0) | 2021.05.19 |
| [BOJ] 백준 1328번 고층 빌딩 (Java) (0) | 2021.05.17 |
| [BOJ] 백준 3344번 N-Queen (백트래킹x) (JAVA) (0) | 2021.05.17 |
| [BOJ] 백준 9657번 돌 게임3 (JAVA) (0) | 2021.05.16 |




