비트(bit)
비트(binary digit)는 데이터를 나타내는 최소 단위로 이진수의 한자라인 0 또는 1의 값을 가진다. 부호 없는 N비트 정수형 변수는 N자리의 이진수로 나타낼 수 있다. 이때 비트가 표현하는 값은 2^0 ~ 2^N-1까지이다.
여기서 2^N-1에 해당하는 비트값을 최상위 비트(Most Significant Bit)라 하고, 2^0에 해당하는 비트값을 최하위 비트(Least Significant Bit)라고 한다.
예를 들어 부호없는 4비트 정수형은 네 자리 이진수로 표시할 수 있는 모든 정수를 나타낼 수 있다. 아래 그림과 같이 4칸의 공간에 이진수 0 또는 1을 넣은 모든 경우의 수를 의미한다. 이때 비트가 표현하는 값은 2^0~2^3이다.

여기서는 2^3이 최상위 비트이고 2^0에 해당하는 비트값(1)이 최하위이다.
비트 연산자 (java 기준)
비트 연산자는 피연산자의 각 비트들을 대상으로 연산이 이루어지며 총 4개의 연산자가 있다.
| 구분 | 연산자 | 의미 | 설명 |
| 비트연산자 | & | 비트 단위의 AND | 두 정수를 한 비트씩 비교하면서 양쪽 비트가 모두 1이면 결과도 1이고 나머지는 0을 반환 |
| | | 비트 단위의 OR | 두 정수를 한 비트씩 비교하면서 양쪽 비트 중 하나라도 1이면 결과가 1이고 나머지는 0을 반환 | |
| ^ | XOR(배타적 OR) | 두 정수를 한 비트씩 비교하면서 양쪽 비트가 서로 다르면 1, 같으면 0을 반환 | |
| ~ | NOT | 정수 하나의 각 비트를 1이면 0, 0이면 1로 바꾸는 연산 | |
| 비트 이동연산자 | << | 정수 a를 왼쪽으로 b비트 만큼 이동 (빈자리는 0으로 채워짐, MSB가 1이 되면 음수로 바뀜) | |
| >> | 정수 a를 오른쪽으로 b비트 만큼 이동 (빈자리는 정수 a의 MSB와 같은 값으로 채워짐) | ||
| >>> | 정수 a를 오른쪽으로 b비트 만큼 이동 (빈자리는 0으로 채워짐) | ||
예제로 보면 다음과 같다.
public static void main(String[] args) {
int x = 10; // 2진수로 변환시 1010
int y = 12; // 2진수로 변환시 1100
System.out.println("x = \t" + Integer.toBinaryString(x));
System.out.println("y = \t" + Integer.toBinaryString(y));
System.out.println("x|y = \t" + Integer.toBinaryString(x|y));
System.out.println("x&y = \t" + Integer.toBinaryString(x&y));
System.out.println("x^y = \t" + Integer.toBinaryString(x^y));
System.out.println("~x = \t" + Integer.toBinaryString(~x)); // int는 4byte = 32bit이기때문에 앞에 28개의 1이 출력됨
int a = -127; // 1111 1111 1111 1111 1111 1111 1000 0001
int shift_a = a>>1; // 1111 1111 1111 1111 1111 1111 1100 0000
int ns_shift_a = a>>>1; // 0111 1111 1111 1111 1111 1111 1100 0000
System.out.println("a =\t" +a+","+ Integer.toBinaryString(a));
System.out.println("a>>1 =\t" +(a>>1)+","+ Integer.toBinaryString(a>>1));
System.out.println("a>>>1 =\t" +(a>>>1)+","+ Integer.toBinaryString(a>>>1));
}
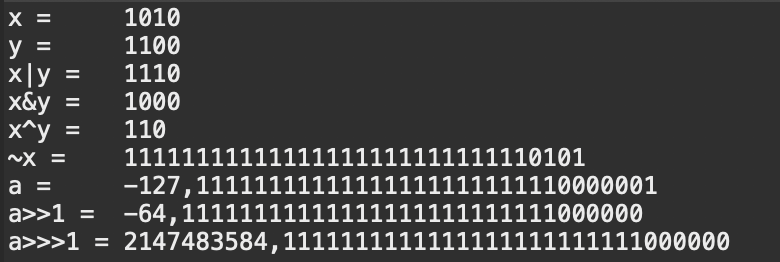
toBinaryString() 메서드는 단지 비트연산자가 컴퓨터 내부에서 어떻게 처리되는지 문자열로 표현해주기 위해 사용했다.
비트마스크 (bit mask)
컴퓨터는 모든 CPU는 이진수를 이용해 모든 자료를 표현한다. 이진수를 이용해 연산을 하면 매우 빠르게 연산이 가능하고 이 특징을 이용해 자료구조 쓰는 기법을 비트마스크(bit mask)라고 한다.
- 이진수는 0 또는 1을 이용하므로 하나의 비트(bit)가 표현할 수 있는 경우는 두 가지이다.
- 보통 어떤 비트가 1이면 "켜져 있다"라고 말하며, 0이면 "꺼져 있다"라고 말한다.
비트마스크 장점
1. 다른 자료 구조에 비해 수행 시간이 더 빠르다.
→ 비트마스크 연산은 bit 연산이기 때문에 O(1)에 구현되는 것이 많다. 따라서 다른 자료구조를 이용하는 것보다 훨씬 빠르게 동작하게 된다.
2. 비트 연산자를 사용하여 코드가 더 간결해진다.
→ 위에 설명한 다양한 집합 연산들을 비트연산자로 한 줄로 작성할 수 있기 때문에 일반 데이터를 반복문, 조건문으로 비교했을 때보다 훨씬 간결하다.
3. 비트마스크를 사용하여 더 작은 메모리를 사용할 수 있다.
→ 개인적으로, 비트마스크를 이용하는 가장 큰 이유라고 생각한다.
간단한 예시로, bit가 10개인 경우에는 각 bit당 두 가지 경우를 가지기 때문에 2^10가지의 경우를 10bit 이진수 하나로 표현이 가능하다. (ex. 10개의 발전소 중 1,3,4,5번 발전소 on -> 0000 0111 01)
→ 이처럼 하나의 정수로 매우 많은 경우의 수를 표현할 수 있기 때문에 메모리 측면에서 효율적이며, 더 많은 데이터를 미리 계산해서 저장해 둘 수 있는 장점이 있다. (DP에 매우 유용하다)
비트마스크를 이용한 집합 구현
비트마스크를 이용한 집합 구현은 가장 대표적이고, 자주 쓰이는 방법이다. 하나의 bit가 하나의 데이터 상태를 의미한다. bit가 1이면 해당 원소가 집합에 포함되어 있다는 의미이고, 0이면 포함되어 있지 않다는 의미이다. 따라서, N비트는 N개의 원소를 갖는 집합의 부분집합들을 모두 표현할 수 있다.
A를 10개의 집합의 상태를 나타내는 변수라고 가정하고 연산을 살펴보자. (0번째 ~ 9번째 원소)
| 연산 | 사용 예시 |
| 공집합과 꽉 찬 집합 구하기 | A = 0; / A = (1 << 10) - 1; |
| 원소 추가 | A |= (1 << k); |
| 원소 삭제 | A &= ~(1 << k); |
| 원소의 포함 여부 확인 | if((A & (1 << k)) == (1 << k)) |
| 원소의 토글(toggle) | A ^= (1 << k); |
| 두 집합에 대해서 연산 | A | B → A와 B의 합집합 A & B → A와 B의 교집합 A & (~B) → A에서 B를 뺀 차집합 A ^ B → A와 B중 하나에만 포함된 원소들의 집합 |
| 집합의 크기 구하기 | int bitCount(int A){ if(A == 0) return 0; return A%2 + bitCount(A / 2); } [내장 명령어] gcc/g++ → __builtin_popcount(A) visual C++ → __popcnt(A) Java → Integer.bitCount(A) |
| 최소 원소 찾기 | int first = A & (-A); |
| 최소 원소 지우기 | A &= (A - 1); |
| 모든 부분 집합 순회하기 | for (int subset = A ; subset>0; subset = ((subset - 1) & A)){ } |
공집합과 꽉 찬 집합 구하기
☛ 기본적으로 공집합은 bit가 모두 꺼진 상황이기 때문에 상수 0이 공집합을 표현한다. 반대로 꽉 찬 집합은 bit가 모두 켜진 상황이기 때문에 1111111111(2) 의 값으로 표현한다.
원소 추가
☛ A 집합에 특정 원소를 추가하는 방법이다. 원소에 해당하는 bit만 켜야 하기 때문에 해당 bit를 항상 1로 만드는 연산이 필요하기 때문에 따라서 OR 연산을 이용한다.
원소 삭제
☛ A 집합에 포함된 특정 원소를 삭제하는 방법이다. A에 k번째 원소의 포함 여부와 상관없이 해당 bit를 끄기 위해서는 AND 연산을 이용해야 한다.
1<<k : k번째가 켜진 상태
^(1<<k) : k번째만 꺼진 상태
A &= ^(1<<k); : A 집합에 담긴 k번째 상태 off
+
A -= (1<<k); :이는 A에 반드시 k번째 원소가 포함되어 있는 경우에만 가능하다. 만약 포함되어 있지 않은 상태에서 삭제 연산을 하게 되면 데이터가 망가진다.
원소의 포함 여부 확인
☛ A 집합에 특정 원소가 포함되어 있는지 확인하는 방법이다. k번째 원소가 포함되어 있는지 확인하고 싶다면, k번째 bit가 켜져 있는지만 확인하면 된다.
원소의 토글
☛ A 집합에 해당 원소가 빠져있는 경우에는 추가하고, 들어있는 경우에는 삭제하는 방법이다. XOR 연산을 이용한다.
두 집합에 대해 연산하기
☛ 두 집합을 A와 B라고 한다면 비트연산자들을 통해서 A와 B의 교집합, 합집합, 차집합 등을 구할 수 있다.
집합의 크기 구하기
☛ 집합에 포함된 원소의 크기를 구한다면 A에서 켜진 bit의 수를 구하면 될 것이다. 직접 모든 비트를 확인하면서 개수를 체크할 수도 있고, 내장 명령어를 이용할 수도 있다.
* 내장 명령어는 최적화되어 구현되어 있기 때문에 직접 모든 비트를 탐색하는 것보다 효율적으로 작동한다. 단, 자바의 경우에는 이 연산이 표준 라이브러리에 포함되어 있지만, gcc와 C++에서 제공하는 함수들은 모두 컴파일러 의존적이므로 유의해야 한다.
최소 원소 찾기
☛ 집합에 포함된 가장 작은 원소 (index가 가장 작은 원소)를 찾는 방법이다. 켜져 있는 bit 중에서 가장 오른쪽에 있는 bit를 찾는 것이다. 비트마스크 뿐만 아니라 펜윅 트리 (Fenwick Tree)에서도 사용되는 기법이다.
비트 A가 있다고하자.
- 가장 오른쪽에 켜져있는 bit를 k라고 하면, 0~k-1의 bit는 모두 0이다.
- 그렇다면 ~A에서는 k번째 bit는 0, 0~k-1의 bit는 모두 1이다.
- ~A + 1을 하게 되면 k번째 bit는 1, 0~k-1의 bit는 모두 0이 된다. k이후의 비트는 아무 변화가 없다.
* ~A + 1 : 컴퓨터가 표현하는 A의 2의 보수 (-A)
→ 따라서, -A와 A를 AND연산을 시키면 k번째 bit만 켜진 상태로 남게 된다.
ex) int first = A & (-A);
A : 1010,
~A+1 (-A) : 0110,
A&(-A) : 0010
최소 원소 지우기
☛ 가장 오른쪽에 켜져 있는 bit를 지우고 싶다면 A-1과 AND시키면 된다. A에서 1을 빼주게 되면 가장 오른쪽에 있던 bit는 0이 되고 그보다 오른쪽에 있는 모든 bit들이 1이 되기 때문이다.
ex) A &= (A-1);
A : 1010,
A-1 : 1001,
A&(A-1) : 1000
모든 부분 집합 순회하기
☛ A의 모든 부분 집합을 탐색하는 방법이다.
ex) A: 1101 탐색
1) 1101 > subset-1 : 1100
2) 1100 > subset-1 : 1011
3) 1001 > subset-1 : 1000
4) 1000 > subset-1 : 0111
5) 0101 > subset-1 : 0100
6) 0100 > subset-1 : 0011
7) 0001 > subset-1 : 0000
비트필드를 이용한 DP문제
위의 비트마스킹을 어느정도 이해했으면 해당 문제를 풀어보자
1562번: 계단 수
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
해당 문제는 boolean으로 0~9의 상태를 하나하나 체크해주면 시간초과가 발생하고 복잡해지므로 비트마스크를 사용하여 계단수를 구해야 한다. dp 3차배열을 사용하여 다음과 같이 비트필드를 사용하여 메모리 공간과 연산을 줄일 수 있다.
i : i자리 숫자 , j 끝나는 숫자 , k 마킹된 숫자
j=9, 10 0000 0000 (9로 끝나는 숫자)
k =1, 10 0000 0001 (9로 끝나는 숫자, 0,9 사용)
k =2, 10 0000 0010 (9로 끝나는 숫자, 1,9 사용)
...
k = 9, 10 0000 1001 (9로 끝나는 숫자, 0,3,9 사용)
...
k = 1023, 11 1111 1111 (9로 끝나는 숫자, 0~9 모두사용)
이해가 쉽게 예시를 몇개 풀어보자
1) 2자리 숫자, 끝자리 숫자는 3, (2,3)이 포함된 수는?
> i=2, j=3, k = 12 (00 0000 1100)
> 답 : 23 , 1개
2) 3자리 숫자, 끝자리 숫자는 4, (2,3,4)이 포함된 수는?
> i=3, j=4, k= 28 (00 0001 1100)
> 답: 234 , 1개
3) 2자리 숫자, 끝자리 숫자 3, (2,3,4)이 포함된 수는?
> 이는 두개의 dp값을 구해야 한다.
> i=2, j=3, k = 12 (00 0000 1100) > 23
> i=2, j=3, k= 24 (00 0001 1000) > 43
> 답 : 23,43 (dp[2][3][12] + dp[2][3][24] = 2개)
점화식 코드
int bit = k | (1<<j); 현재 상태를 나타내는 K에 j(0~9)값을 갖는 상태를 추가해준다
☛ k=6 (0110), j=8(1000) 이면 bit = 14(1110)
☛ (1,2) → (1,2,3)로 3 상태 On
dp[n][num][bit] += dp[n-1][num+1][bit] + dp[n-1][num-1][bit];
☛ 길이가 n-1이고 끝자리 수가 num라고 하면 (끝자리에 num+1이 들어올 경우) + (끝자리에 num-1이 들어올 경우)를 더해주면 된다.
j==0, j==9
☛ 예외) 끝자리가 0이나 9인 경우, 새로운 숫자는 각 1,8밖에 오지 못한다.
// 1<<i : 0~9 비트마스킹
for(int i=1; i<10; i++) {
dp[1][i][1<<i] =1; // 1자리 숫자 0~9값 초기화
}
for(int i=2; i<n+1; i++) {
for(int j=0; j<10; j++) {
for(int k=0; k<1024; k++) { // k = 2^10 (숫자 0~9의 데이터 상태)
int bit = k | (1 << j);
if(j==0) {
dp[i][j][bit] = (dp[i][j][bit] + dp[i-1][j+1][k]) % MOD;
}
else if(j==9) {
dp[i][j][bit] = (dp[i][j][bit] + dp[i-1][j-1][k]) % MOD;
}
else {
dp[i][j][bit] = (dp[i][j][bit] + dp[i-1][j+1][k]+ dp[i-1][j-1][k]) % MOD;
}
}
}
}
'Dot Algo∙ DS > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘] 외판원 순회 문제(TSP: Travelling Salesman Problem) 정리 (Java) (0) | 2021.06.15 |
|---|---|
| [알고리즘] 소수(Prime Number) 구하기 - 에라토스테네스의 체 (Java) (0) | 2021.06.12 |
| [알고리즘] 분할정복 알고리즘 정리 (합병 정렬, 퀵 정렬, 이진 탐색) (Java) (0) | 2021.05.30 |
| [알고리즘] 백트래킹(Backtracking) 가지치기 기법 (Java) (0) | 2021.05.12 |
| [알고리즘] 문자열 매칭 알고리즘 KMP (Java) (0) | 2021.05.11 |




