#17472 다리 만들기 2
난이도 : 골드 2
유형 : 그래프 탐색/ BFS/ 최소 신장 트리 (MST) - 크루스칼
17472번: 다리 만들기 2
첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다.
www.acmicpc.net
▸ 문제

▸ 입력
첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다.
▸ 출력
모든 섬을 연결하는 다리 길이의 최솟값을 출력한다. 모든 섬을 연결하는 것이 불가능하면 -1을 출력한다.
문제 풀이
이 문제를 풀이하는데 꽤 오랜 시간이 걸렸다. 설계와 기본 능력 부족으로 꽤나 고생했다. 그래도 삽질 끝에 해결했다.
* 설계 오류 : 트리 구조를 생각안하고 플로이드 와샬로 접근
* 실수 : break을 return으로...
이 문제는 그래프 탐색 알고리즘(BFS, DFS)과 최소 신장 트리(MST)의 개념을 알고 있으면 풀이가 더 수월해진다.
📚 조건
- 지도 크기 세로 N, 가로 M ( 1 <= N,M <= 10 , 3 <= NxM <= 100)
- 0은 바다 , 1은 땅
- 다리는 한 방향으로만 지어진다. ( +x, -x, +y , -y)
- 교차된 다리는 따로 계산한다.
MEMO) NxM은 최소 3이므로 최소 1x3의 크기의 맵은 나와야 된다. 1 0 0, 1 0 1 은 모두 -1이므로 별로 신경안써도 될 것 같다.
구상
- 일단 섬을 구분지어줘야 한다.
- 그런 다음 섬과 섬사이의 최단 거리(다리)를 구한다.
- 구한 값으로 섬과 섬사이를 잇는 모든 다리 길이의 최솟값를 구하면 된다.
스케치
설계를 대충 스케치했으면 이제 선을 뚜렷하게 그어보자. 각 로직(메소드)에 어떤 알고리즘을 사용할지 정하면 된다.
∙ 1번 로직
모든 그래프를 탐색하면 되므로 DFS, BFS 뭐를 써도 상관없지만 맵의 크기가 엄청 큰거 아니면 그래프 색칠하기는 보통 BFS를 사용하는 것이 더 좋다. 1인 곳을 탐색하여 각 탐색마다 서로 다른 index값을 색칠해주면 된다.
∙ 2번 로직
이 로직 또한 마찬가지로 섬마다 탐색을 들어가서 바다 방향쪽으로 총 4번의 BFS 탐색을 해주고 그 최단 거리를 구해주면 된다.
* 이 로직에서 어이없는 실수로 1시간 삽질했다...
∙ 3번 로직
이 부분에서 살짝 헤맸었다. 난 처음에 플로이드 와샬 알고리즘을 사용하여 각 섬에서의 다른 섬들의 최단거리를 구한 다음 값을 구하려 했지만 그러면 모든 섬들이 연결되어 있는지에 대한 여부를 알 방도가 없었다.
그래서 결국은 Union-find 서로소 집합 구조를 사용해야만 했기 때문에 최소 스패닝 트리의 대표인 크루스칼 알고리즘을 사용했다.
구현
이제 각 로직에 대해 코딩을 해보자.
∙ 1번 로직 코드
브루트포스로 모든 맵을 탐색하면서 map[i][j] = 1인 곳을 찾으면 BFS탐색으로 인접한 땅들을 모두 색칠해주면 된다.
islandCnt =2;
check = new boolean[n][m];
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
if(map[i][j]==1 && !check[i][j]) {
islandIndexing(j, i, islandCnt);
islandCnt++;
}
}
}
static void islandIndexing(int x, int y, int idx) {
q = new LinkedList<>();
q.add(new int[] {x,y});
map[y][x] = idx;
check[y][x] = true;
while(!q.isEmpty()) {
int[] p = q.poll();
int px = p[0];
int py = p[1];
for(int i=0; i<4; i++) {
int nx = px + dx[i];
int ny = py + dy[i];
if(nx<0 || ny <0 || nx > m-1 || ny > n-1 || check[ny][nx]) continue;
if(map[ny][nx]==1) {
map[ny][nx] = idx;
check[ny][nx] = true;
q.add(new int[] {nx,ny});
}
}
}
}
∙ 2번 로직 코드
다리의 종류는 ㅣ, ㅡ 로 총 2가지이고 양방향이다. 그래서 하나의 정점에서 그 네 가지의 다리가 설계되는지 한 번씩 맞춰봐야한다.
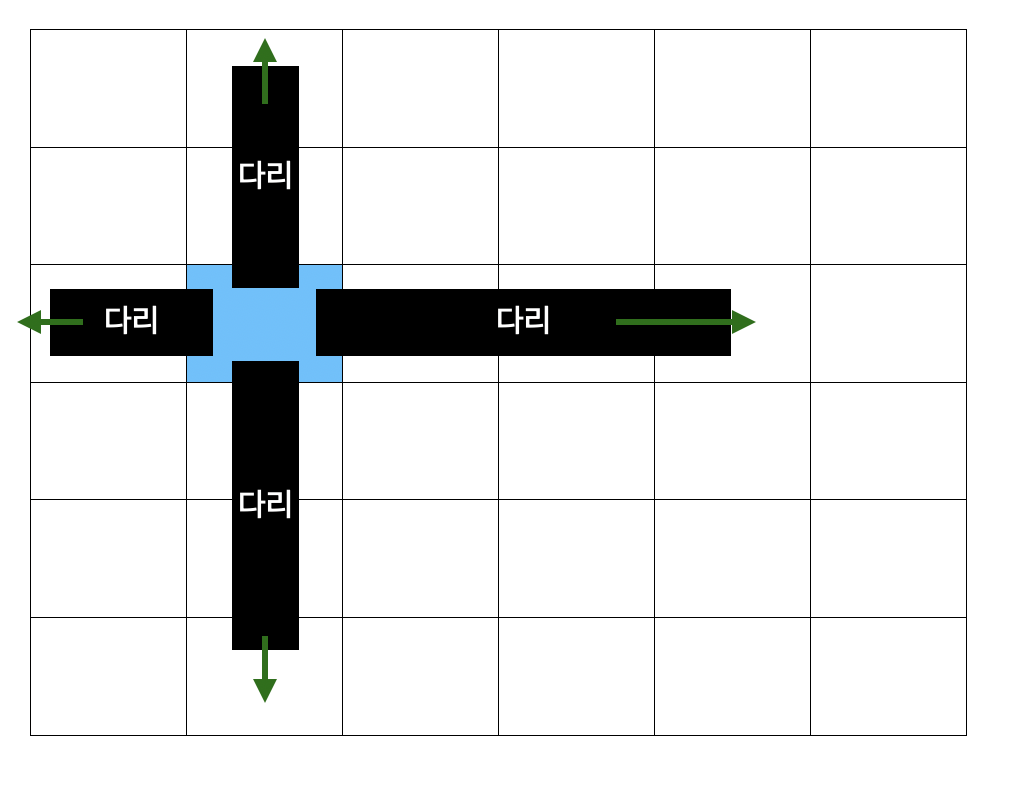
방법은 간단하다. 각 정점마다 for문을 총 4번 돌려 각 방향으로 while문을 돌려 탐색해주면 된다. 그리고 길이가 2 이상 부터 설계가 가능하므로 해당 부분만 조건을 걸어주면 된다. 다리의 조건이 완성되었으면 크루스칼 알고리즘에 사용할 우선순위 큐에 해당 노드 정보와 다리 길이를 저장해주면 된다.
static void makeBridge(int x, int y, int idx) {
q = new LinkedList<>();
check = new boolean[n][m];
for(int d=0; d<4; d++) {
q.add(new int[] {x,y,0});
check[y][x] = true;
while(!q.isEmpty()) {
int[] p = q.poll();
int px = p[0];
int py = p[1];
int move = p[2];
int nx = px + dx[d];
int ny = py + dy[d];
if(nx<0 || ny <0 || nx > m-1 || ny > n-1 || check[ny][nx]) continue;
if(map[ny][nx]!=idx) {
if(map[ny][nx] !=0) {
int from = idx-1;
int to = map[ny][nx]-1;
int bridgeLen = move;
if(bridgeLen>1) {
pq.add(new Node(from, to, bridgeLen));
break;
}
}else {
check[ny][nx] = true;
q.add(new int[] {nx, ny, move+1});
}
}
}
q.clear();
}
}
여기서 어이없는 실수를 했었는데 우선순위 큐에 새로운 정보를 저장하고 return을 시켜버렸다... 이러면 해당 정점에서 다른 방향의 다리는 탐색도 못하고 탐색이 종료되기 때문에 break;를 시켜줘야 한다.
if(bridgeLen>1) {
pq.add(new Node(from, to, bridgeLen));
return;
}
∙ 3번 로직 코드
이제 새로운 문제라고 생각하면 된다. 이번 문제는 크루스칼 알고리즘문제이다. 이 문제에서는 그래프의 정점과 간선이 주어졌고 모든 정점을 포함하는 최소 신장 트리(크루스칼 사용)를 구하면 된다.
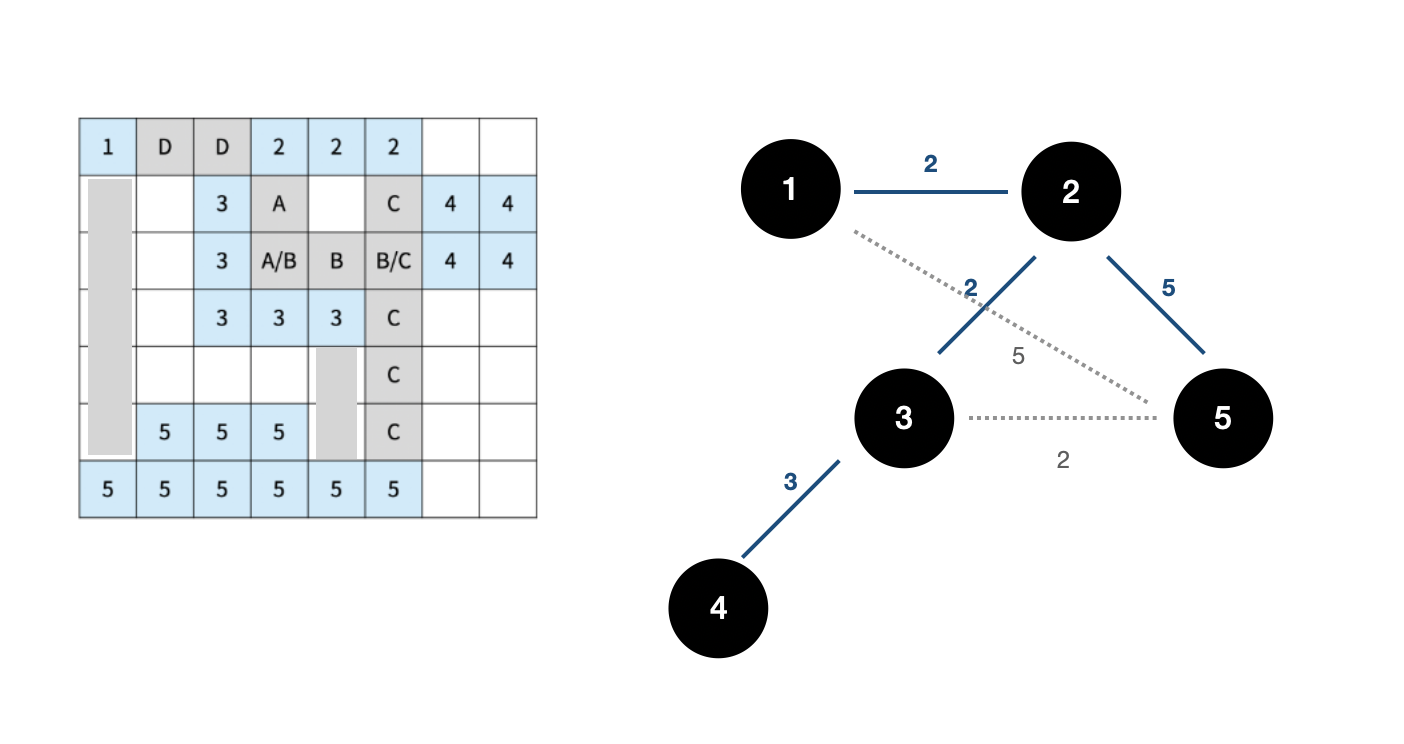
해당 그래프와 간선의 정보는 2번 로직에서 우선순위 큐에 저장해뒀다. 이제 그것을 꺼내어 다리길이가 짧은 순부터 조회를 하여 사이클이 발생하지 않는 경우에만 집합에 포함시키면 된다.
static int shortestPath() {
int sum =0;
int size = pq.size();
for(int i=0; i< size; i++) {
Node node = pq.poll();
int x = node.from;
int y = node.to;
if(find(x) != find(y)) {
System.out.println(x+"," +y + " 연결 " + node.value);
sum += node.value;
union(x,y);
}
}
int rx = parents[1];
for(int i=2; i<islandCnt; i++) {
if(rx != find(parents[i])) {
System.out.println("연결 x ");
return 0;
}
}
return sum;
}
다리 길이가 짧은 것부터 조회하면서 싸이클이 생기기 전까지 모든 노드를 union 합쳐준다. 모든 섬들이 연결되었으면 다리의 총 길이를 반환해준다. 만약 0이 반환되면 섬과 섬사이의 다리가 모두 연결되지 않은 것이므로 -1을 출력해주면 된다.
islandCnt--;
parents = new int[islandCnt];
for(int i=1; i<islandCnt; i++) {
parents[i] = i;
}
int answer = shortestPath();
System.out.println(answer == 0 ? -1 : answer);
전체 풀이 코드
개념은 다 알고있는데 문제를 풀지 못했다면 아마 설계 능력과 집중력 부족 때문일 것이다. 개념에 맞게 코딩을 했는데 풀리지 않는다면 어떤 조건을 놓치지는 않았는지 코드에 어떤 실수가 없는지 꼼꼼하게 점검하자.
import java.io.*;
import java.util.*;
public class Main {
static class Node implements Comparable<Node>{
int to;
int from;
int value;
public Node(int to, int from, int value) {
this.to = to;
this.from = from;
this.value = value;
}
@Override
public int compareTo(Node o) {
return this.value - o.value;
}
}
static int n,m, islandCnt;
static int[][] map;
static int[] parents;
static Queue<int[]> q;
static PriorityQueue<Node> pq = new PriorityQueue<>(); ;
static boolean[][] check;
static int[] dx = {-1, 1, 0, 0};
static int[] dy = {0, 0, -1, 1};
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
map = new int[n][m];
for(int i=0; i<n; i++) {
st = new StringTokenizer(br.readLine());
for(int j=0; j<m; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
}
}
islandCnt =2;
check = new boolean[n][m];
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
if(map[i][j]==1 && !check[i][j]) {
islandIndexing(j, i, islandCnt);
islandCnt++;
}
}
}
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
if(map[i][j]!=0) {
makeBridge(j, i, map[i][j]);
}
}
}
islandCnt--;
parents = new int[islandCnt];
for(int i=1; i<islandCnt; i++) {
parents[i] = i;
}
int answer = shortestPath();
System.out.println(answer == 0 ? -1 : answer);
}
// 1번 로직 (그래프 색칠)
static void islandIndexing(int x, int y, int idx) {
q = new LinkedList<>();
q.add(new int[] {x,y});
map[y][x] = idx;
check[y][x] = true;
while(!q.isEmpty()) {
int[] p = q.poll();
int px = p[0];
int py = p[1];
for(int i=0; i<4; i++) {
int nx = px + dx[i];
int ny = py + dy[i];
if(nx<0 || ny <0 || nx > m-1 || ny > n-1 || check[ny][nx]) continue;
if(map[ny][nx]==1) {
map[ny][nx] = idx;
check[ny][nx] = true;
q.add(new int[] {nx,ny});
}
}
}
}
// 2번 로직 (그래프 연결)
static void makeBridge(int x, int y, int idx) {
q = new LinkedList<>();
check = new boolean[n][m];
for(int d=0; d<4; d++) {
q.add(new int[] {x,y,0});
check[y][x] = true;
while(!q.isEmpty()) {
int[] p = q.poll();
int px = p[0];
int py = p[1];
int move = p[2];
int nx = px + dx[d];
int ny = py + dy[d];
if(nx<0 || ny <0 || nx > m-1 || ny > n-1 || check[ny][nx]) continue;
if(map[ny][nx]!=idx) {
if(map[ny][nx] !=0) {
int from = idx-1;
int to = map[ny][nx]-1;
int bridgeLen = move;
if(bridgeLen>1) {
pq.add(new Node(from, to, bridgeLen));
break;
}
}else {
check[ny][nx] = true;
q.add(new int[] {nx, ny, move+1});
}
}
}
q.clear();
}
}
// 3번 로직 (최소 신장트리 -크루스칼)
static int shortestPath() {
int sum =0;
int size = pq.size();
for(int i=0; i< size; i++) {
Node node = pq.poll();
int x = node.from;
int y = node.to;
if(find(x) != find(y)) {
sum += node.value;
union(x,y);
}
}
int rx = parents[1];
for(int i=2; i<islandCnt; i++) {
if(rx != find(parents[i])) {
// System.out.println("연결 x ");
return 0;
}
}
return sum;
}
static int find(int x) {
if(parents[x] == x) return x;
int rx = find(parents[x]);
return rx;
}
static void union(int x, int y) {
x = find(x);
y = find(y);
if(x<y) {
parents[y]=x;
}
else {
parents[x] =y;
}
}
}
솔직히 사람이라면 집중력이 깨질 수 있고 어떠한 조건을 충분히 빠트릴 수 있다. 그래서 설계가 중요하다고 느낀게 이러한 실수를 해결하는데 설계가 잘 되어 있으면 고치기 굉장히 수월하다. 예로 들면, 1번 로직까지는 완벽하다 싶으면 2번 로직부터 검수를 시작하면 되고 1,2번 로직까지는 완벽하다고 생각하면 3번 로직 부분만 고치면 된다.
'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 10159번 저울 (Java) (0) | 2021.06.11 |
|---|---|
| [프로그래머스] 2021 카카오 / 메뉴 리뉴얼 (Java) (0) | 2021.06.11 |
| [BOJ] 백준 17142번 연구소 3 (Java) (0) | 2021.06.09 |
| [BOJ] 백준 2228번 구간 나누기 (Java) (0) | 2021.06.09 |
| [BOJ] 백준 1963번 소수 경로 (Java) (0) | 2021.06.08 |




