#1517 버블 소트
난이도 : 골드 1
유형 : 자료 구조 / 좌표 압축 / 세그먼트 트리 || 합병 정렬
1517번: 버블 소트
첫째 줄에 N(1≤N≤500,000)이 주어진다. 다음 줄에는 N개의 정수로 A[1], A[2], …, A[N]이 주어진다. 각각의 A[i]는 0≤|A[i]|≤1,000,000,000의 범위에 들어있다.
www.acmicpc.net
▸ 문제
N개의 수로 이루어진 수열 A[1], A[2], …, A[N]이 있다. 이 수열에 대해서 버블 소트를 수행할 때, Swap이 총 몇 번 발생하는지 알아내는 프로그램을 작성하시오.
버블 소트는 서로 인접해 있는 두 수를 바꿔가며 정렬하는 방법이다. 예를 들어 수열이 3 2 1 이었다고 하자. 이 경우에는 인접해 있는 3, 2가 바뀌어야 하므로 2 3 1 이 된다. 다음으로는 3, 1이 바뀌어야 하므로 2 1 3 이 된다. 다음에는 2, 1이 바뀌어야 하므로 1 2 3 이 된다. 그러면 더 이상 바꿔야 할 경우가 없으므로 정렬이 완료된다.
▸ 입력
첫째 줄에 N(1≤N≤500,000)이 주어진다. 다음 줄에는 N개의 정수로 A[1], A[2], …, A[N]이 주어진다. 각각의 A[i]는 0≤|A[i]|≤1,000,000,000의 범위에 들어있다.
▸ 출력
첫째 줄에 Swap 횟수를 출력한다
문제 풀이
📚 조건
- 배열의 크기 N ( 1<= N <= 500,000)
- 원소 범위 A[i] ( 0 <= |A[i]| <= 1,000,000,000)
버블 정렬 연산횟수를 구하는 문제이지만 버블 정렬을 사용해서는 안된다. 해당 문제의 N의 범위가 상당히 크므로 버블소트의 시간복잡도는 O(N^2)이기 때문에 시간초과가 발생한다.
버블 정렬
배열 [6 4 3 5 2 1]을 버블 정렬을 사용해서 오름차순 시켜보자.

버블 정렬은 배열 인덱스 0부터 선형탐색으로 n-1까지 움직여 정렬하는 방식으로 동작한다.





과정을 보면 원소들은 앞에 있는 원소들 중 자신보다 낮은 수의 만큼 연산하는 것을 알 수 있다.
- 원소 6은 {4,3,5,2,1}보다 크기 때문에 총 5번
- 원소 5는 {2,1}보다 크기 때문에 총 2번
- 원소 4는 {3,2,1}보다 크기 때문에 총 3번
- 원소 3은 {2,1}보다 크기 때문에 총 2번
- 원소 2는 {1}보다 크기 때문에 총 1번
- 원소 1은 0번
→ 연산 횟수는 총 13이다.
결국 버블 정렬 연산횟수는 자신보다 앞에 있는 수의 갯수를 세어주면 되는 것을 발견할 수 있다. 이 패턴을 이해했으면 이젠 세그먼트 트리로 해당 문제를 풀이할 수 있게 된다.
세그먼트 트리
세그먼트를 이용해서 앞에 자신보다 큰 값이 몇개나 들어있는지 트리의 구조를 이용해서 구하면 O(logN)으로 탐색가능하다. 해당 N번 반복하면 되므로 총 O(NlogN)으로 로직을 짤 수 있다.
좌표 압축하기
원소 범위 A[i] ( 0 <= |A[i]| <= 1,000,000,000) 이기 때문에 트리 원소로 담기에는 너무 부담되는 크기이다. 그래서 해당 배열 원소에 index를 붙여줘서 N의 최대 크기인 50만으로 제한을 해준 다음에 트리에 담아 줄 것이다.
for(int i=0; i<n; i++) {
elements[i] = Integer.parseInt(st.nextToken());
}
// <K, V> = <segment tree index, elements in queue (중복 값 처리)>
Map<Long, Queue<Integer>> pos = new HashMap<>();
for (int i = 0; i < n; i++) {
pos.computeIfAbsent(elements[i], k -> new LinkedList<>()).offer(i);
}| idx | 0 | 1 | 2 | 3 | 4 | 5 |
| elements | 6 | 4 | 3 | 5 | 2 | 1 |
elements배열을 오름차순으로 정렬해준다. 작은 수 부터 세그먼트 트리에 넣어주어야 자신보다 앞의 구간 [idx+1 ~ n-1]에 자신보다 작은 수가 몇 개 있는지 카운트할 수 있기 때문이다. 물론 역으로도 탐색이 가능하다.
1. 원소 1 카운트
먼저 원소 1보다 앞에 있는 수는 없으므로 카운트는 0이다. 그리고 원소 1의 elements의 위치는 5이므로 해당 위치에 트리 +1을 업데이트 해준다.
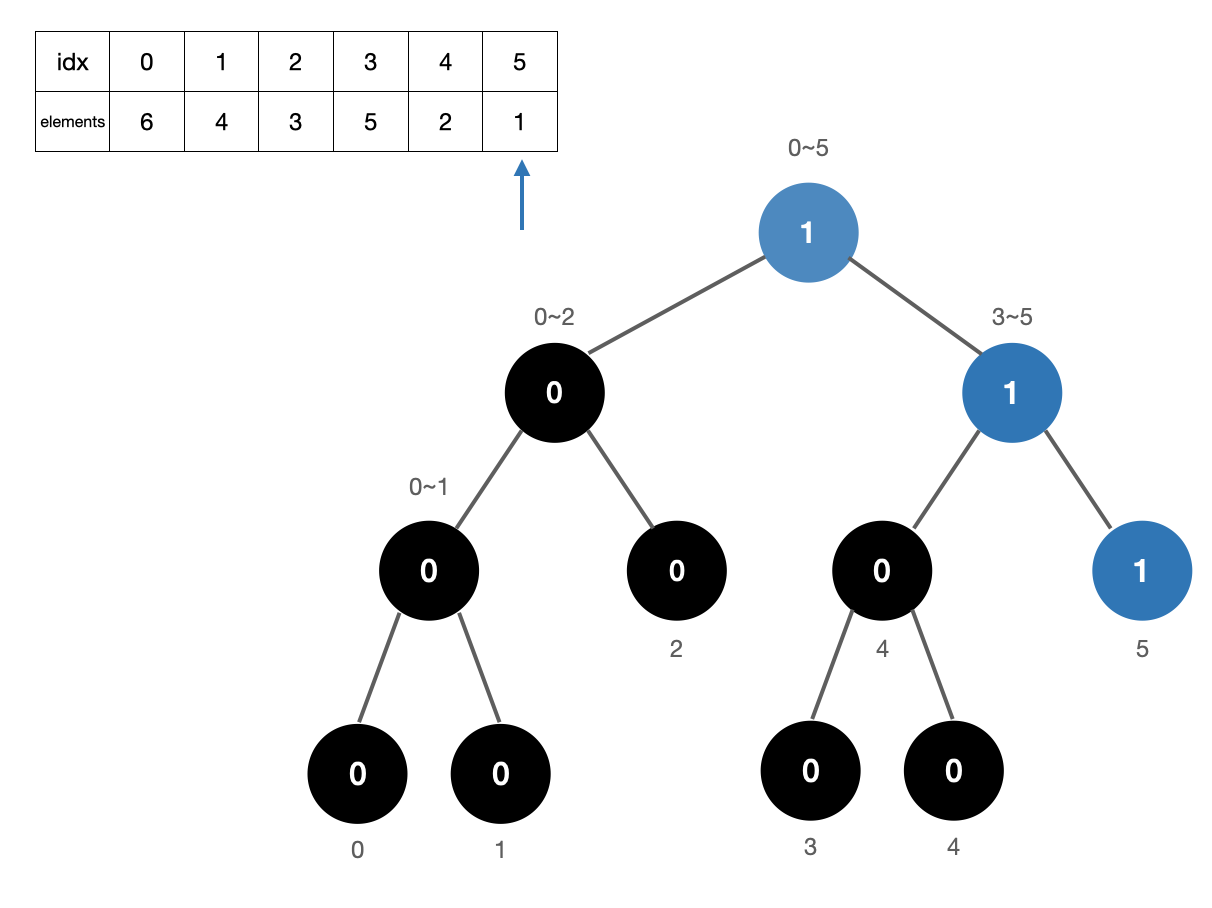
2. 원소 2 카운트
원소 2의 위치는 4이므로 (4,5]의 구간에 수를 카운트해준다. 카운트 +1
그리고나서 4번 위치에 해당하는 트리를 업데이트 해준다. 중요한 건 카운트를 먼저 해주고나서 트리를 업데이트해줘야 한다.
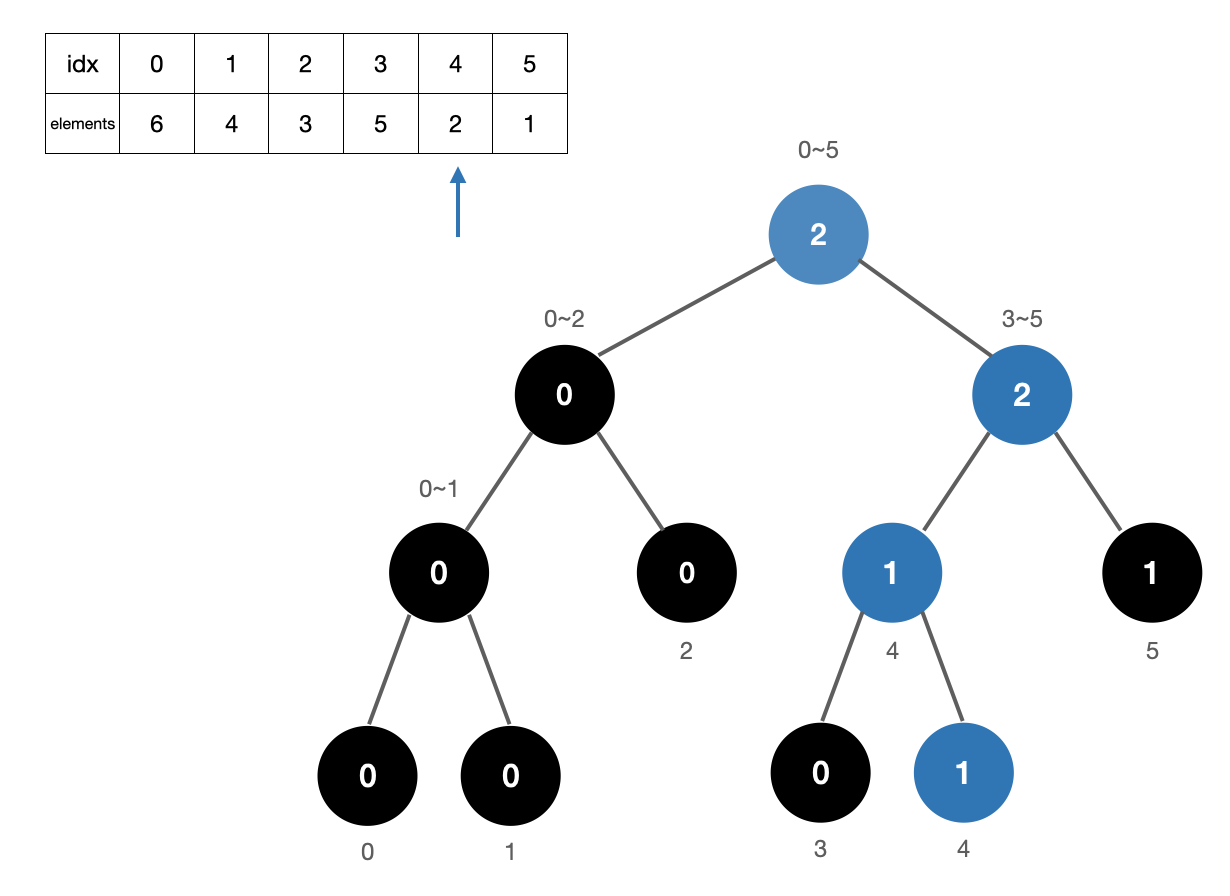
3. 원소 3 카운트
원소 3의 위치는 2이므로 [3,5] 구간을 카운트해준 다음 트리를 업데이트 해준다. 카운트 +2 (3번노드)
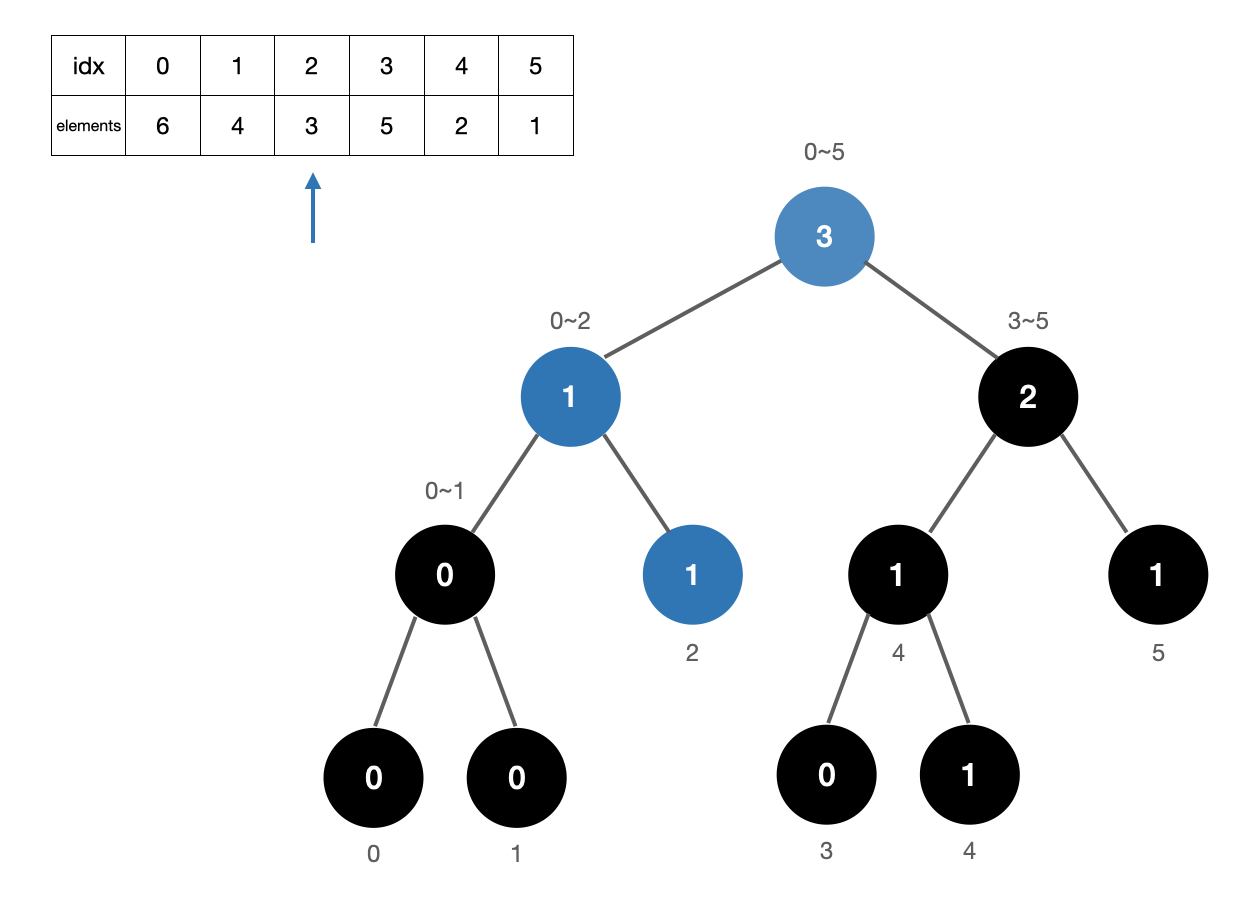
3. 원소 4 카운트
원소 4의 위치는 1이므로 [2,5] 구간을 카운트해준 다음 트리를 업데이트 해준다. 카운트 +3 (5번, 3번노드)
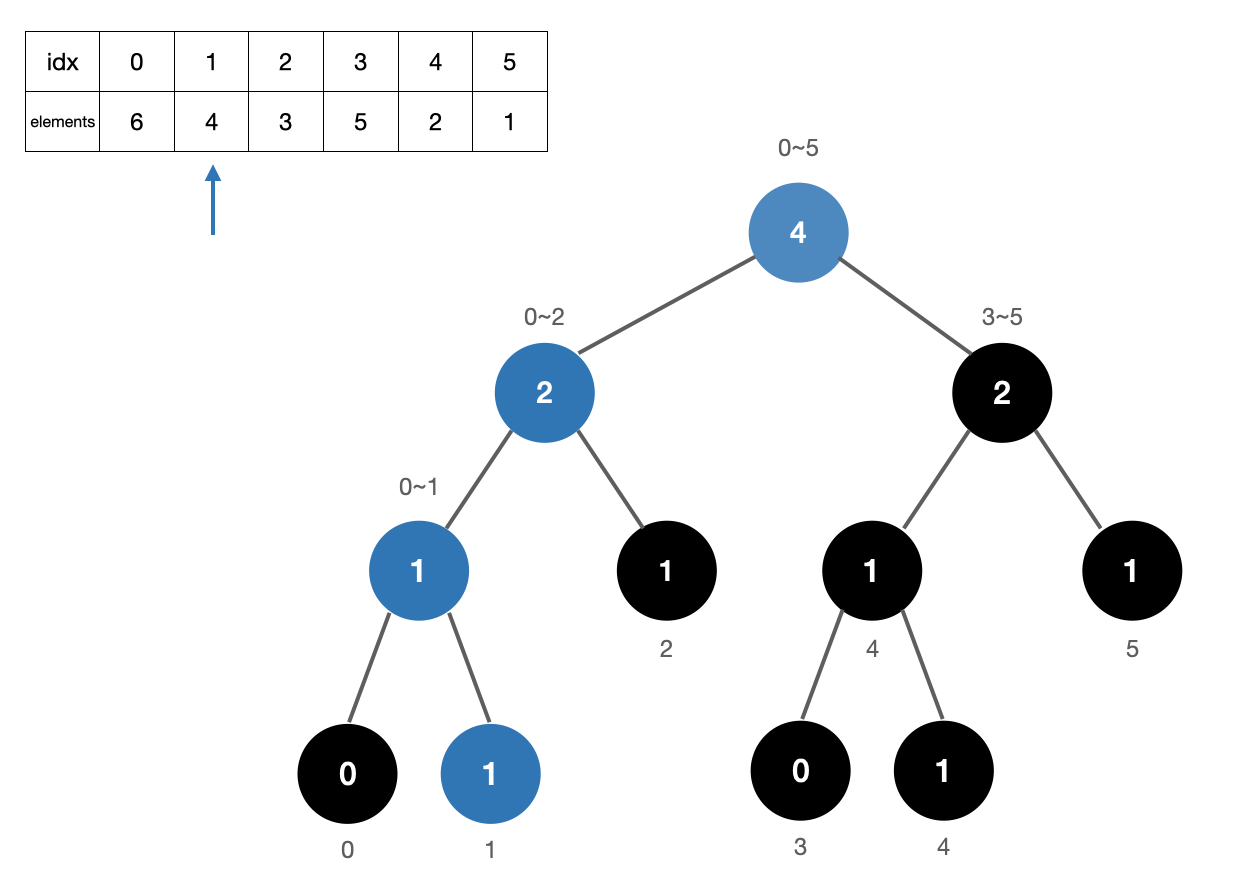
3. 원소 5 카운트
원소 5의 위치는 3이므로 [4,5] 구간을 카운트해준 다음 트리를 업데이트 해준다. 카운트 +2 (7번, 13번노드)
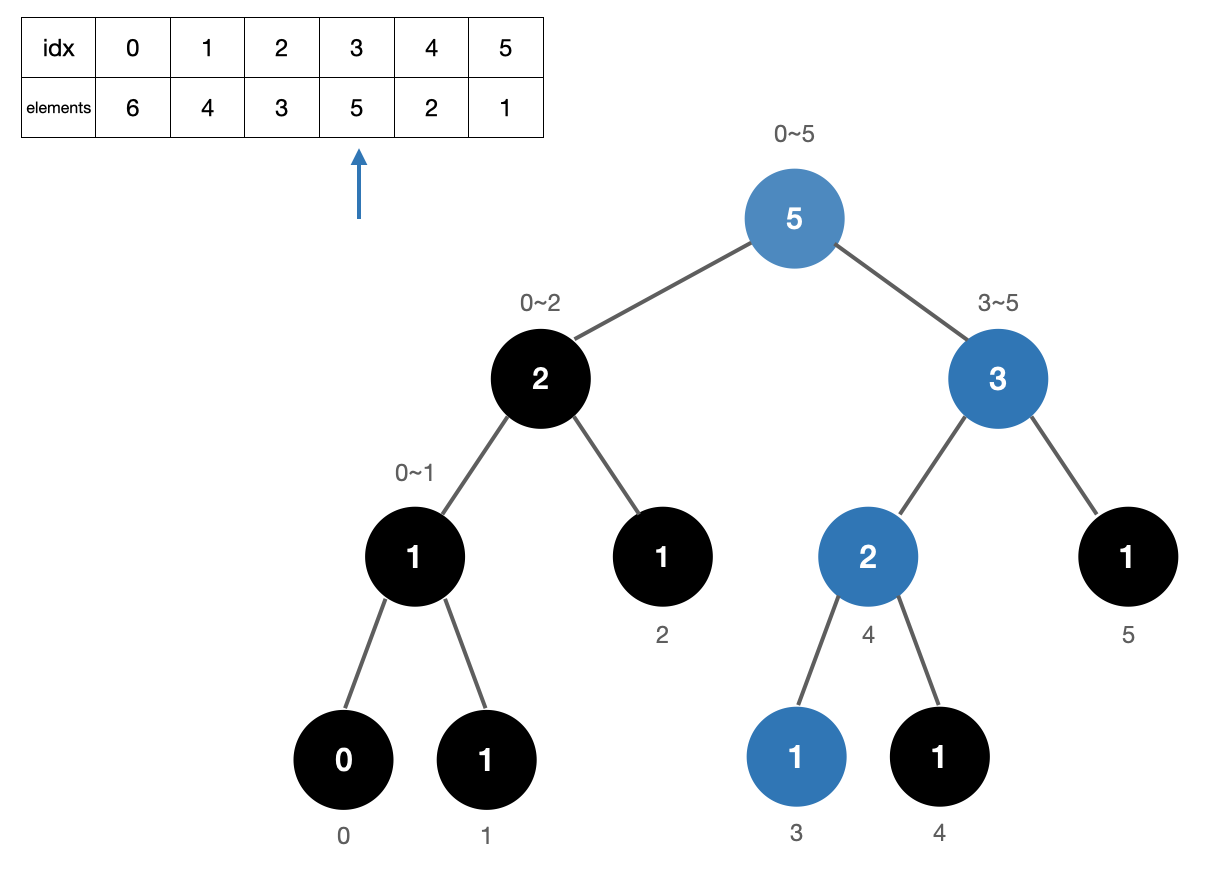
3. 원소 6 카운트
원소 6의 위치는 0이므로 [1,5] 구간을 카운트해준 다음 트리를 업데이트 해준다. 카운트 +5 (3번, 5번, 9번 노드)
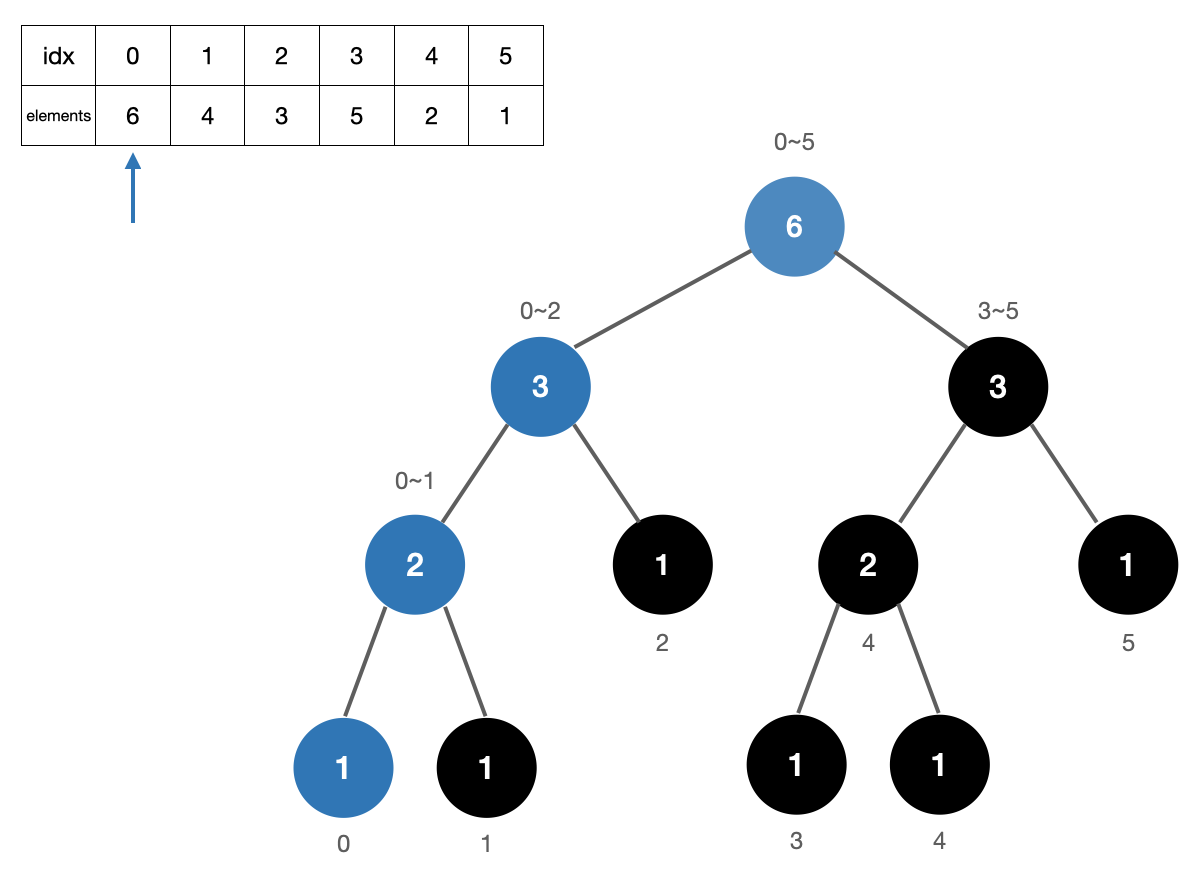
연산과정 테이블
| elements order | idx | 구간 (idx+1 ~ n-1) | 연산횟수 |
| 1 | 5 | 0 | |
| 2 | 4 | 5~5 | +1 |
| 3 | 2 | 3~5 | +2 |
| 4 | 1 | 2~5 | +3 |
| 5 | 3 | 4~5 | +2 |
| 6 | 0 | 1~5 | +5 |
풀이 코드 (세그먼트 트리) - 2024.01 update 중복 요소 처리
import java.io.*;
import java.util.*;
public class Main {
static int n;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
long[] elements = new long[n];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<n; i++) {
elements[i] = Integer.parseInt(st.nextToken());
}
// <K, V> = <segment tree index, elements in queue (중복 값 처리)>
Map<Long, Queue<Integer>> pos = new HashMap<>();
for (int i = 0; i < n; i++) {
pos.computeIfAbsent(elements[i], k -> new LinkedList<>()).offer(i);
}
long[] index = elements.clone();
Arrays.sort(index);
long[] tree = new long[getTreeSize()];
long ans =0;
for(int i=0; i<n; i++) {
int idx = pos.get(index[i]).poll();
ans += sum(tree,0, n-1, 1, idx+1, n-1);
update(tree, 0, n-1, 1, idx, 1);
}
System.out.println(ans);
}
static int getTreeSize() {
int h = (int)Math.ceil(Math.log(n)/Math.log(2))+1;
return (int)Math.pow(2, h);
}
static long sum(long[] tree, int start, int end, int node, int left, int right) {
if(end < left || right < start ) return 0;
if(left <= start && end <= right) {
return tree[node];
}
int mid = (start+end)/2;
return sum(tree, start, mid, node*2, left, right) + sum(tree, mid+1, end, node*2+1, left, right);
}
static void update(long[] tree, int start, int end, int node, int idx, int dif) {
if(start == end ) {
tree[node] = dif;
return;
}
int mid = (start+end)/2;
if(idx <= mid) update(tree, start, mid, node*2, idx, dif);
else update(tree, mid+1, end, node*2+1, idx, dif);
tree[node] = tree[node*2]+tree[node*2+1];
}
}
합병 정렬
합병 정렬도 위와 같은 방식으로 로직을 설계해주면 O(NlogN)으로 버블 정렬의 연산횟수를 구할 수 있다.
주어진 배열을 모두 divide한 후 다시 merge하는 과정에서 elements[i] > elements[j] 앞에 자신보다 큰 수 있는 경우 그만큼 count해주면 된다.
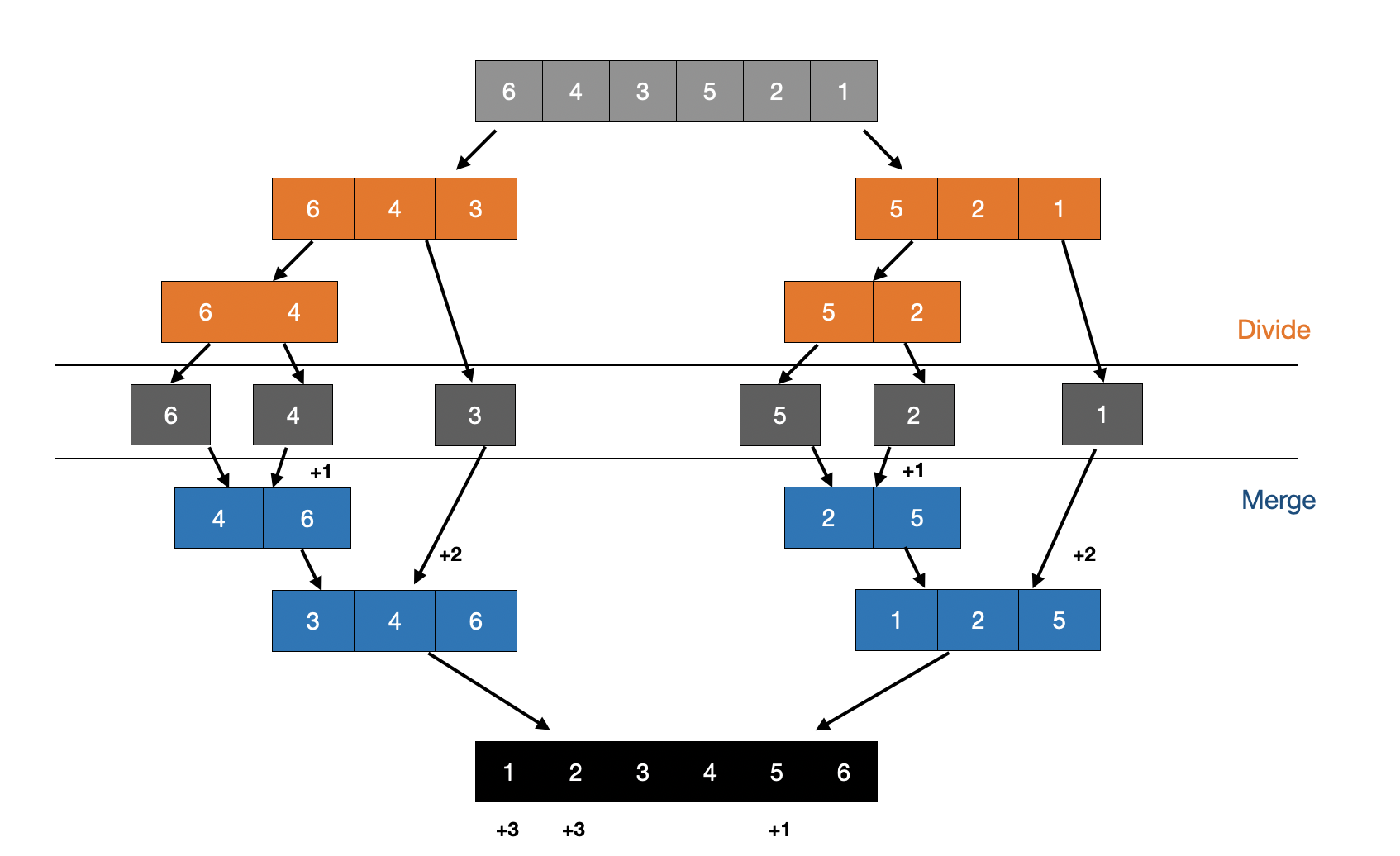
풀이 코드 (합병 정렬)
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static long ans;
static long[] elements, sorted;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
elements = new long[n];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<n; i++) {
elements[i] = Integer.parseInt(st.nextToken());
}
sorted = new long[n];
divide(0,n-1);
System.out.println(ans);
}
static void divide(int low, int high) {
if(low < high) {
int mid = (low+high)/2;
divide(low, mid);
divide(mid+1, high);
merge(low, mid, high);
}
}
static void merge(int low, int mid, int high) {
int i = low; // 왼쪽 시작 인덱스
int j= mid+1; // 오른쪽 시작 인덱스
int k = low; // sorted배열 인덱스
while(i<= mid && j <= high) {
if(elements[i] <= elements[j]){
sorted[k] = elements[i];
i++;
}else { // elements[i] > elements[j] 앞에 자신보다 큰 수 있는 경우
sorted[k] = elements[j];
j++;
ans += (mid+1-i); // 연산횟수 카운트
}
k++;
}
// 나머지 합병과정 처리
while(i <= mid) {
sorted[k] = elements[i];
i++;
k++;
}
while(j <= high) {
sorted[k] = elements[j];
j++;
k++;
}
for(int m=low; m<high+1; m++) {
elements[m] = sorted[m];
}
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 1197번 최소 스패닝 트리 (Java) (0) | 2021.07.12 |
|---|---|
| [BOJ] 백준 10422번 괄호 (Java) (1) | 2021.07.11 |
| [BOJ] 백준 10999번 구간 합 구하기2 (Java) (0) | 2021.07.08 |
| [BOJ] 백준 11003번 최솟값 찾기 (Java) (0) | 2021.07.07 |
| [BOJ] 백준 2470번 두 용액 (Java) (0) | 2021.07.06 |




