#3 자물쇠와 열쇠
난이도 : LEVEL3
유형 : 그래프, 시뮬레이션
코딩테스트 연습 - 자물쇠와 열쇠
[[0, 0, 0], [1, 0, 0], [0, 1, 1]] [[1, 1, 1], [1, 1, 0], [1, 0, 1]] true
programmers.co.kr
▸ 문제
고고학자인 "튜브"는 고대 유적지에서 보물과 유적이 가득할 것으로 추정되는 비밀의 문을 발견하였습니다. 그런데 문을 열려고 살펴보니 특이한 형태의 자물쇠로 잠겨 있었고 문 앞에는 특이한 형태의 열쇠와 함께 자물쇠를 푸는 방법에 대해 다음과 같이 설명해 주는 종이가 발견되었습니다.
잠겨있는 자물쇠는 격자 한 칸의 크기가 1 x 1인 N x N 크기의 정사각 격자 형태이고 특이한 모양의 열쇠는 M x M 크기인 정사각 격자 형태로 되어 있습니다.
자물쇠에는 홈이 파여 있고 열쇠 또한 홈과 돌기 부분이 있습니다. 열쇠는 회전과 이동이 가능하며 열쇠의 돌기 부분을 자물쇠의 홈 부분에 딱 맞게 채우면 자물쇠가 열리게 되는 구조입니다. 자물쇠 영역을 벗어난 부분에 있는 열쇠의 홈과 돌기는 자물쇠를 여는 데 영향을 주지 않지만, 자물쇠 영역 내에서는 열쇠의 돌기 부분과 자물쇠의 홈 부분이 정확히 일치해야 하며 열쇠의 돌기와 자물쇠의 돌기가 만나서는 안됩니다. 또한 자물쇠의 모든 홈을 채워 비어있는 곳이 없어야 자물쇠를 열 수 있습니다.
열쇠를 나타내는 2차원 배열 key와 자물쇠를 나타내는 2차원 배열 lock이 매개변수로 주어질 때, 열쇠로 자물쇠를 열수 있으면 true를, 열 수 없으면 false를 return 하도록 solution 함수를 완성해주세요.
▸ 제한사항
- key는 M x M(3 ≤ M ≤ 20, M은 자연수)크기 2차원 배열입니다.
- lock은 N x N(3 ≤ N ≤ 20, N은 자연수)크기 2차원 배열입니다.
- M은 항상 N 이하입니다.
- key와 lock의 원소는 0 또는 1로 이루어져 있습니다.
- 0은 홈 부분, 1은 돌기 부분을 나타냅니다.
문제 풀이
카카오 기출 그래프 시뮬레이션 문제 중간에 잠깐 딴생각하면 골치아파진다. 효율성 테스트가 없어도 구현하는데 4중 포문이 나와서 적잖이 당황했다. 결국 중간에 방향을 틀어 초등학생 때 많이 사용했던 트레팔지(?) 약간 투명한 종이를 생각하면서 LOCK과 KEY를 하나하나 맞대가면서 움직이도록 구현했다.
구상
Key의 움직을 먼저 파악했다. Key는 시계방향으로 360도 회전을 할 수 있고 상하좌우로 m-1칸까지 이동할 수 있다. 원래 처음에 90도씩 시계 방향으로 회전하는 메소드와 상하좌우로 0~M-1칸씩 이동하는 메소드를 구현했었지만 삽입 삭제부분이 복잡해져 방향을 바꿨다.
Lock과 Key를 트레팔지에 그린 후 겹쳐서 한칸씩 대비하도록 설계하였다. 그래서 Key를 회전하는 메소드는 그래도 냅두고 이동 메소드를 제거 후 Key를 m+2*(m-1)크기를 가지는 행렬로 확장을 해주는 메소드를 작성했다.
다음과 같이 Lock과 Key가 있다고하자. 조건을 보면 알 수 있듯 M은 N보다 클 수 없다는 가정하에 이루어져야 한다.

다음 그림과 같이 각 모서리 지점까지 겹치게끔 두개의 Lock, Key 종이를 대조를 해보면 된다. Lock(0,0) Key(0,0) 좌표를 시작으로 상하좌우로 N+M-1칸씩 이동해보면서 매칭이 되는지 대조해보면 된다. Lock이아닌 Key를 확장시킨 이유는 계속해서 Key를 회전시키며 다뤄왔었는데 이를 위해 Lock까지 변경하게 되면 로직이 더 복잡해질 것 같았기 때문이다.
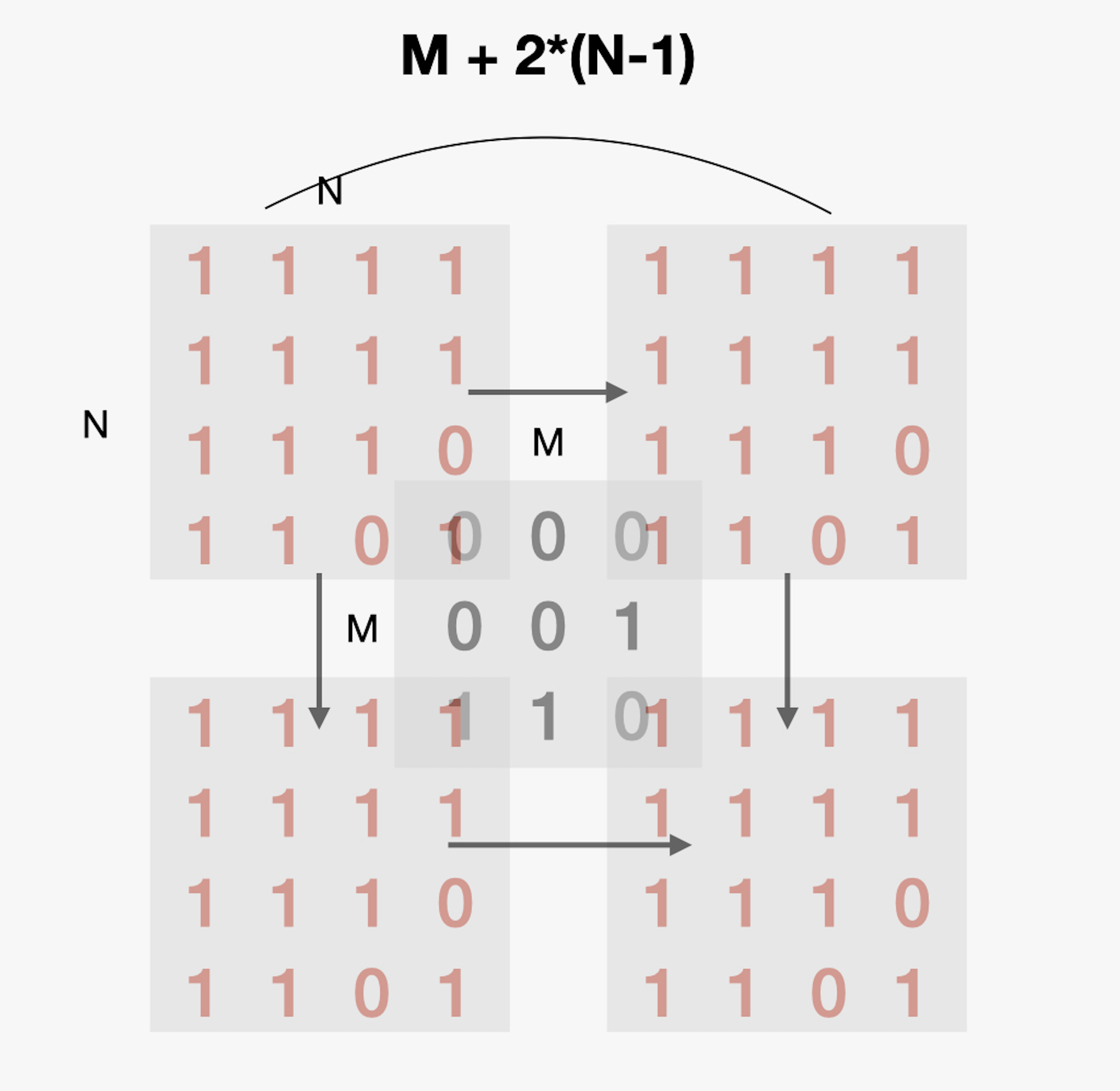
설계
- Key를 0, 90, 180, 270 총 4번의 회전을 이룬다. turnKey(tmp);
- Key를 m+2*(n-1)의 크기로 확장하고 [0+(n-1)][0+(n-1)]을 시작으로 키를 복사한다. extendKeyToLock(tmp);
- 확장된 Key와 Lock을 대조해보며 일치하는지 확인한다.
- if(lock[y][x] == key[i+y][j+x])이면, false를 반환한다.
- Key로 Lock을 해제할 수 있으면 true를 반환하고 모든 로직을 종료한다.
- 모든 로직이 끝나도 true가 리턴되지 않으면 false를 반환한다.
풀이 코드
class Solution {
static int n,m;
public boolean solution(int[][] key, int[][] lock) {
n = lock.length; // NxN
m = key.length; // MxM
int t =0;
int[][] tmp = getCopyKey(key);
while(t<4) {
int[][] exKey = extendKeyToLock(tmp); //(M+2*(N-1))x(M+2*(N-1))
boolean res = matchingKeyToLock(exKey,lock);
if(res) return true;
tmp = turnKey(tmp);
t++;
}
return false;
}
static boolean matchingKeyToLock(int[][] key, int[][] lock) {
for(int i=0; i<m+n-1; i++) {
for(int j=0; j<m+n-1; j++) {
boolean flag = true;
out:
for(int y=0; y<n; y++) {
for(int x=0; x<n; x++) {
if(lock[y][x] == key[i+y][j+x]) {
flag = false;
break out;
}
}
}
if(flag) return true;
}
}
return false;
}
static int[][] extendKeyToLock(int[][] src){
int[][] extendKey = new int[m+2*(n-1)][m+2*(n-1)];
for(int i=0; i<m; i++) {
for(int j=0; j<m; j++) {
extendKey[i+n-1][j+n-1] = src[i][j];
}
}
return extendKey;
}
static int[][] turnKey(int[][] src) {
int[][] trunKey = new int[m][m];
int y = m-1;
for(int i=0; i<m; i++) { // y
for(int j=0; j<m; j++) { // x
trunKey[j][y] = src[i][j];
}
y--;
}
return trunKey;
}
static int[][] getCopyKey(int[][] src) {
int[][] copy = new int[m][m];
for(int i=0; i<m; i++) {
for(int j=0; j<m; j++) {
copy[i][j] = src[i][j];
}
}
return copy;
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [프로그래머스] 2020 카카오 #4 가사 검색 (Java) (0) | 2021.09.07 |
|---|---|
| [BOJ] 백준 7785번 회사에 있는 사람 (Java) (0) | 2021.09.06 |
| [프로그래머스] 2020 카카오 #2 괄호 변환 (Java) (0) | 2021.09.04 |
| [프로그래머스] 2020 카카오 #1 문자열 압축 (Java) (0) | 2021.09.04 |
| [BOJ] 백준 2449번 전구 (Java) (0) | 2021.09.03 |




