#1693 트리 색칠하기
난이도 : 플레 2
유형 : 트리 DP / DFS
1693번: 트리 색칠하기
n개의 정점으로 이루어진 트리가 있다. 이 트리의 각 정점을 색칠하려고 한다. 색칠을 할 때에는 1, 2, 3, …, n번 색깔 중에 하나로 색칠하여야 한다. 각 색깔을 사용하여 한 개의 정점을 색칠할 때
www.acmicpc.net
▸ 문제
n개의 정점으로 이루어진 트리가 있다. 이 트리의 각 정점을 색칠하려고 한다. 색칠을 할 때에는 1, 2, 3, …, n번 색깔 중에 하나로 색칠하여야 한다. 각 색깔을 사용하여 한 개의 정점을 색칠할 때마다 1, 2, …, n의 비용이 든다. 즉, i번 색깔로 한 개의 정점을 색칠하면 i만큼의 비용이 든다는 것이다.
또한 정점에 색칠을 할 때에, 주어진 트리 상에서 인접해 있는 서로 다른 두 정점은 서로 다른 색깔로 칠해야 한다. 이를 만족하면서, 전체 정점을 색칠하는데 드는 총 비용을 최소화 하려 한다. 최소 비용을 계산하는 프로그램을 작성하시오.
▸ 입력
첫째 줄에는 정점 및 색깔의 개수 n(1 ≤ n ≤ 100,000)이 주어진다. 다음 n-1개의 줄에는 각 줄에 두 개의 정수로 주어진 트리 상에서 연결되어 있는 두 정점의 번호가 주어진다.
▸ 출력
첫째 줄에 최소 비용을 출력한다.
문제 풀이
최대 정점의 수가 10만개, 색칠할 수 있는 색의 수 최대 10만개-1이다. 브루트포스 알고리즘으로 모든 색을 대입하여 최솟값을 구하면 시간초과가 발생한다. 처음에 리프노드에 1을 색칠하고 주고 부모노드에는 자식노드가 색칠하지 않은 수 중 가장 작은 수를 색칠하는 알고리즘을 작성하였다.
하지만 41%에서 실패했다. ↓
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
import java.util.List;
import java.util.Map;
import java.util.Set;
import java.util.StringTokenizer;
public class Main {
static int n;
static Map<Integer, Set<Integer>> map;
static List<Integer>[] list;
static int[] dp;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
map = new HashMap<>();
list = new ArrayList[n+1];
dp = new int[n+1];
for(int i=1; i<n+1; i++) {
list[i] = new ArrayList<>();
}
StringTokenizer st = null;
for(int i=0; i<n-1; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
list[a].add(b);
list[b].add(a);
}
traversal(1,-1);
int cost=0;
for(int i=1; i<n+1; i++) {
cost += dp[i];
}
System.out.println(cost);
}
static void traversal(int idx, int pa) {
// leaf 노드
if(list[idx].size()==1) {
dp[idx] = 1;
}
for(int nxt : list[idx]) {
if(nxt !=pa) {
traversal(nxt, idx);
}
}
if(pa!=-1) {
Set<Integer> data;
if(!map.containsKey(pa)) {
data = new HashSet<>();
data.add(dp[idx]);
map.put(pa, data);
}else {
data = map.get(pa);
if(data.add(dp[idx])) {
map.put(pa, data);
}
}
int nv =0;
for(int i=1; i<n+1; i++) {
if(!map.get(pa).contains(i)) {
nv = i;
break;
}
}
dp[pa] = nv;
}
}
}
해당 코드의 반례는 다음과 같다.
반례)
17
1 2
1 3
1 4
1 5
3 6
3 7
4 8
4 9
8 13
5 10
5 11
5 12
10 14
10 15
11 16
14 17
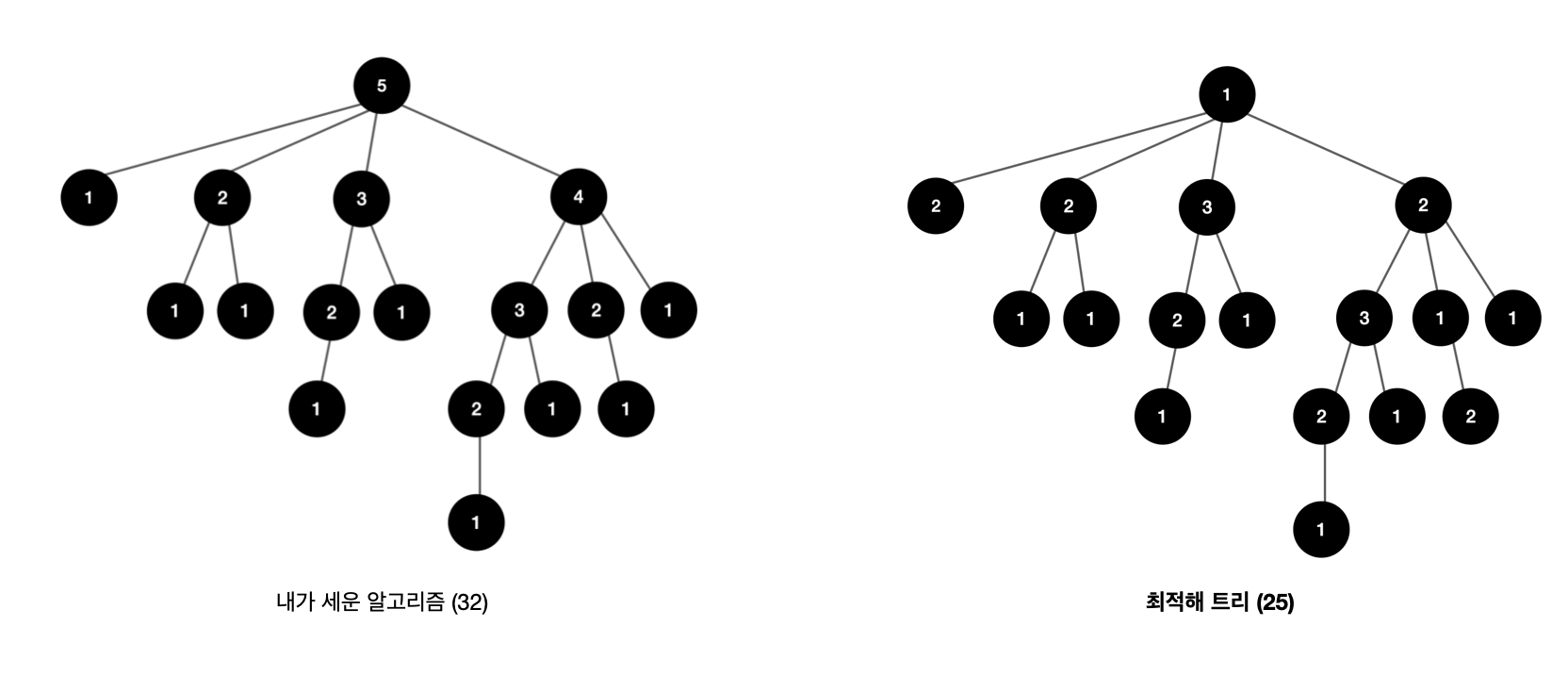
위의 시행착오를 겪고 최적해를 찾는 방식이 뭐가 있을까 생각을 해봤지만 도무지 생각이 나질 않았다. 질문 글을 참고해보니 해당 문제를 트리DP로 대입하는 색의 수를 logN으로 줄여 연산횟수를 줄여내는 방식으로 풀이를 하였다. 그래서 이를 참고하여 풀이를 다시 하였다.
koosaga님의 답변에 의하면 논리는 다음과 같다.
T(N) : 트리에 N개의 색을 사용했을 때 나오는 트리의 최소 비용이라고 정의한다.
1. T(1)은 1개의 색을 사용하므로 1임을 알 수 있다.
2. N>=1, T(i) >= T(i-1) + T(i-2) + ... + T(1) 이라고 하자.
최소 비용을 가지는 T(i)의 트리를 그려보면 해당 트리에는 i번의 색을 가진 노드가 하나 존재할 것이다. 그러면 이 트리에 인접한 노드들은 i-1, i-2, i-3, ... ,1의 색을 가진다. (인접한 노드가 i-1~1의 색을 모두 가지지 않는다면 위의 노드가 i번 색을 가질 이유가 없다.

따라서, i색을 가지는 노드의 서브트리의 크기는 최소 T(i-1)이상이다. (여기서, T(i)의 최소트리크기를 minT(i)라 하자.)
minT(1)의 최소 트리 크기는 자기 자신 하나이므로 1,
minT(2)은 minT(1) + 1 = 2,
minT(3)은 minT(1)+minT(2)+1 = 4,
minT(4)은 minT(1)+minT(2)+minT(3)+1 = 8,
... ,
T(i)는 min(T(1...i-1)) + 1 = (2^(i-1)-1) +1 = 2^(i-1)이다.
따라서, T(N)의 최소 트리 크기는 2^(N-1)임을 알 수 있다.
해당 문제의 N의 최댓값은 10만이므로 log2(100,000) = 16.60964... <17이다. 그래서 가지는 색의 경우의 수를 최대 17로 넣고 DFS탐색을 하여 최소비용을 가지는 트리를 구하면 된다.
설계
- 트리 데이터를 인접리스트에 저장한다. list[a].add(b); list[b].add(a);
- 트리 순회를 통해 1번 노드를 루트노드를 가지는 트리 데이터로 정제시킨다. makeTreeData(1,-1);
- 정제된 데이터를 사용하여 DFS탐색을 통해 최소 비용을 가지도록 트리를 색칠해준다. tmp = Math.min(tmp, painting(nxt,i));
- dp[cur][color] : cur노드의 서브트리들이 가지는 최소 비용을 더해서 저장한다. dp[cur][color] += tmp;
- cur노드 서브트리의 최솟값에 해당 노드의 최소비용이 드는 color를 더해준다. dp[cur][color] += color;
- 이렇게 1번 노드가 1~17색을 가지는 경우를 모두 조사하여 가장 적은 비용이 드는 값을 출력한다. res = Math.min(res, painting(1,c));
풀이 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;
public class Main {
static int n, INF = 987654321;
static List<Integer>[] list;
static List<Integer>[] tree;
static int[][] dp;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
list = new ArrayList[n+1];
tree = new ArrayList[n+1];
for(int i=1; i<n+1; i++) {
list[i] = new ArrayList<>();
tree[i] = new ArrayList<>();
}
StringTokenizer st = null;
for(int i=0; i<n-1; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
list[a].add(b);
list[b].add(a);
}
makeTreeData(1,-1);
dp = new int[n+1][18];
for(int i=1; i<n+1; i++) {
Arrays.fill(dp[i], -1);
}
int res = INF;
for(int c=1; c<18; c++) {
res = Math.min(res, painting(1,c));
}
System.out.println(res);
}
static int painting(int cur, int color) {
if(dp[cur][color] != -1) return dp[cur][color];
dp[cur][color]=0;
int cnt =0;
for(int nxt : tree[cur]) {
int tmp = INF;
for(int i=1; i<18; i++) {
if(color!=i) {
tmp = Math.min(tmp, painting(nxt,i));
}
}
dp[cur][color] += tmp;
}
return dp[cur][color] += color;
}
static void makeTreeData(int idx, int pa) {
for(int nxt : list[idx]) {
if(nxt != pa){
tree[idx].add(nxt);
makeTreeData(nxt ,idx);
}
}
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 1213번 팰린드롬 만들기 (Java) (0) | 2021.10.09 |
|---|---|
| [BOJ] 백준 6416번 트리인가? (Java) (0) | 2021.10.08 |
| [프로그래머스] 위클리 챌린지 9주차 전력망 둘로 나누기 (Java) (0) | 2021.10.06 |
| [BOJ] 백준 15900번 나무 탈출 (Java) (0) | 2021.10.05 |
| [BOJ] 백준 16437번 양 구출 작전 (Java) (0) | 2021.10.04 |




