#1289 트리의 가중치
난이도 : 플레 3
유형 : 트리 / 수학
1289번: 트리의 가중치
첫째 줄에 트리의 정점의 개수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 N-1개의 줄에 대해 각 줄에는 세 개의 정수 A, B, W(1 ≤ A, B ≤ N, 0 ≤ W ≤ 1,000)가 입력되는데 이는 A점과 B점이 연결되어 있고 이
www.acmicpc.net
▸ 문제
트리는 N개의 정점과 N-1개의 간선으로 구성된 그래프이다. 트리의 성질 중 하나는 어느 두 정점 간에도 유일하게 하나의 경로가 존재한다는 것이다.
트리의 모든 간선에 음이 아닌 정수인 가중치가 배정되었다. ‘경로의 가중치’란 경로에 해당하는 간선의 곱으로 정의된다. 또한 ‘트리의 가중치’는 트리 상에 가능한 모든 경로에 대해 ‘경로의 가중치’의 합을 의미한다. 문제는 트리가 주어졌을 때 ‘트리의 가중치’를 구하는 것이다.
▸ 입력
첫째 줄에 트리의 정점의 개수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 N-1개의 줄에 대해 각 줄에는 세 개의 정수 A, B, W(1 ≤ A, B ≤ N, 0 ≤ W ≤ 1,000)가 입력되는데 이는 A점과 B점이 연결되어 있고 이 간선의 가중치는 W라는 것을 의미한다.
▸ 출력
첫째 줄에 트리의 가중치를 1,000,000,007로 나눈 나머지를 출력한다.
문제 풀이
크기가 작으면 플로이드 와샬 알고리즘을 사용하여 모든 정점의 길이를 구해준 다음 더하면 되는데 해당 문제는 범위가 커서 메모리 초과가 발생한다. 해당 문제를 풀기 위해서는 일단 트리의 가중치를 어떻게 구하는지 샅샅이 파악해야 한다.
트리 가중치 구하기
먼저 자식 노드가 2개 이상인 트리는 가중치를 다음과 같이 구할 수 있다.
- treeWeight = a+b+c+d+ab+ac+ad+bc+bd+cd;
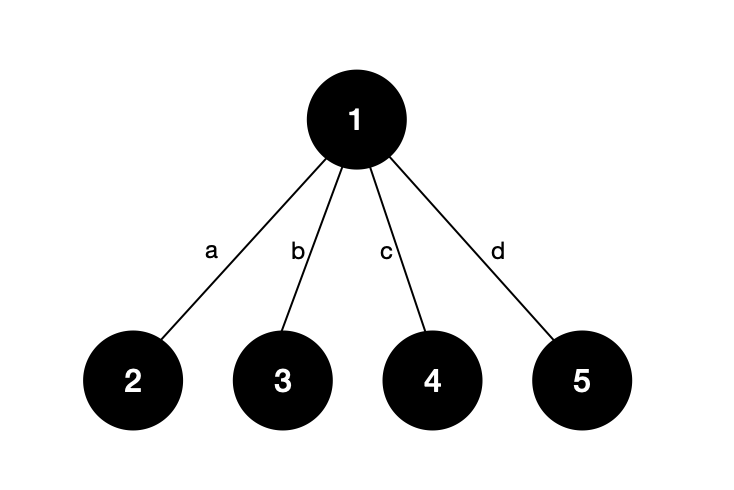
1번 노드를 기준으로 DFS탐색하는 관점에서 다시 살펴보자. DFS탐색을 하게되면 한 정점씩 방문하게 되는데 이전에 방문한 서브트리의 값을 저장하면 루트 노드를 경유하여 생기는 간선의 가중치까지 구해줄 수 있다. (ex. 2 → 1 → 4, 3 → 1 → 5)
- 1 → 2, 2번노드르 끝나는 가중치 a
- 1 → 3, 2 → 3, 3번노드르 끝나는 가중치 b + ab = (1+a)*b
- 1 → 4, 2→ 4, 3→ 4, 4번노드르 끝나는 가중치 : c + ac + bc = (1+a+b)*c
- 1 → 5, 2→ 5, 3→ 5, 4→ 5, 5번노드르 끝나는 가중치 : d + ad + bd + cd = (1+a+b+c)*d
- 해당 값들을 모두 더하면 위에서 구한 a+b+c+d+ab+ac+ad+bc+bd+cd인 트리의 가중치를 구할 수 있다.
시뮬레이션
그럼 다음 트리의 가중치는 어떻게 구하면 될까? 이 또한 위의 방식대로 Top-down과정으로 풀이해주면 된다.

부분 트리를 나누면 다음과 3개의 트리로 나눠볼 수 있다. 그러면 3개의 트리 가중치를 구해서 더해주면 된다. DFS로 후위순회 탐색을 하게 되면 왼쪽아래 파란색 트리부터 시작하여 오른쪽 트리를 거친후 마지막으로 빨간색 트리의 가중치를 구하게 된다. 여기서 구해지는 모든 가중치의 합을 구하면 답을 도출해낼 수 있다.

탐색 과정을 자세히 나타내면 다음과 같다.

각 트리의 왼쪽 가중치 간선을 a부터 오른쪽으로 b, c...의 가중치라고 했을 때 구해지는 식은 다음과 같다. 아래 과정은 각 트리의 계산 과정만 직관적으로 나타내기 위해 2번,6번,1번 트리 순으로 표현한 것이니 주의하자. (원래의 탐색과정은 위의 그림과 같이 1,2,3,4순대로 이뤄져야 한다.)
2번 트리
- 2번 트리 가중치 : a+(1+a)*b + (1+a+b)*c = 17
- a = 1
- b = 2
- c = 3
6번 트리
- 6번 트리 가중치 : a+(1+a)*b = 5
- a = 1
- b = 2
1번 트리
- 1번 트리 가중치 : a+ (1+a)*b = 196
- a = (1+2+3)*2+2 = 14
- b = (1+2)*3 + 3 = 12
따라서, 모든 트리의 합을 구하면 17 + 5 + 196 = 215가 됨을 알 수 있다.
설계
- 주어진 각 노드의 데이터와 가중치를 인접리스트 배열에 저장한다.
- dfs탐색을 통해 트리 전체를 탐색하여 가중치를 구해준다.
- idx → nxt 간선에 가중치를 곱해준다.
- total : 현재까지 구한 해당 노드를 끝점으로 하는 가중치를 더해준다.
- 만약 n번 노드를 탐색했다하면 ((1...n-1) → n 번 노드 가중치 간선) = (1+2+...n-1)*n을 나타낸다.
- res : 해당 트리의 간선 크기를 더하여 저장해준다. (ex. 1+a+b...)
- 해당 트리 탐색이 끝났으면 해당 트리 모든 간선의 합(res)을 부모노드로 보내준다.
- return res;
풀이 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;
public class Main {
static long total;
static List<int[]>[] list;
static final int MOD = 1_000_000_007;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
list = new ArrayList[n+1];
for(int i=1; i<n+1; i++) {
list[i] = new ArrayList<>();
}
StringTokenizer st;
for(int i=0; i<n-1; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
list[u].add(new int[] {v,w});
list[v].add(new int[] {u,w});
}
dfs(1,0);
System.out.println(total);
}
static long dfs(int idx, int pa) {
long res = 1;
for(int[] nxt : list[idx]) {
if(nxt[0] != pa) {
long w = ((dfs(nxt[0], idx))*nxt[1])%MOD;
total = (total+res*w)%MOD;
res = (res+w)%MOD;
}
}
return res;
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 17073번 나무 위의 빗물 (Java) (0) | 2021.10.24 |
|---|---|
| [BOJ] 백준 14675번 단절점과 단절선 (Java) (0) | 2021.10.23 |
| [BOJ] 백준 19535번 ㄷㄷㄷㅈ (Java) (0) | 2021.10.21 |
| [BOJ] 백준 1240번 노드사이의 거리 (Java) (0) | 2021.10.20 |
| [BOJ] 백준 13511번 트리와 쿼리2 (Java) (0) | 2021.10.19 |




