#2873 롤러코스터
난이도 : 플레 3
유형 : 그리디 / 구현
2873번: 롤러코스터
첫째 줄에 가장 가장 큰 기쁨을 주는 롤러코스터는 가장 왼쪽 위 칸부터 가장 오른쪽 아래 칸으로 어떻게 움직이면 되는지를 출력한다. 위는 U, 오른쪽은 R, 왼쪽은 L, 아래는 D로 출력한다. 정답
www.acmicpc.net
▸ 문제
상근이는 우리나라에서 가장 유명한 놀이 공원을 운영하고 있다. 이 놀이 공원은 야외에 있고, 다양한 롤러코스터가 많이 있다.
어느 날 벤치에 앉아있던 상근이는 커다란 황금을 발견한 기분이 들었다. 자신의 눈 앞에 보이는 이 부지를 구매해서 롤러코스터를 만든다면, 세상에서 가장 재미있는 롤러코스터를 만들 수 있다고 생각했다.
이 부지는 직사각형 모양이고, 상근이는 R행 C열의 표 모양으로 나누었다. 롤러코스터는 가장 왼쪽 위 칸에서 시작할 것이고, 가장 오른쪽 아래 칸에서 도착할 것이다. 롤러코스터는 현재 있는 칸과 위, 아래, 왼쪽, 오른쪽으로 인접한 칸으로 이동할 수 있다. 각 칸은 한 번 방문할 수 있고, 방문하지 않은 칸이 있어도 된다.
각 칸에는 그 칸을 지나갈 때, 탑승자가 얻을 수 있는 기쁨을 나타낸 숫자가 적혀있다. 롤러코스터를 탄 사람이 얻을 수 있는 기쁨은 지나간 칸의 기쁨의 합이다. 가장 큰 기쁨을 주는 롤러코스터는 어떻게 움직여야 하는지를 구하는 프로그램을 작성하시오.
▸ 입력
첫째 줄에 R과 C가 주어진다. (2 ≤ R, C ≤ 1000) 둘째 줄부터 R개 줄에는 각 칸을 지나갈 때 얻을 수 있는 기쁨이 주어진다. 이 값은 1000보다 작은 양의 정수이다.
▸ 출력
첫째 줄에 가장 가장 큰 기쁨을 주는 롤러코스터는 가장 왼쪽 위 칸부터 가장 오른쪽 아래 칸으로 어떻게 움직이면 되는지를 출력한다. 위는 U, 오른쪽은 R, 왼쪽은 L, 아래는 D로 출력한다. 정답은 여러 가지 일 수도 있다.
문제 풀이
매트릭스 구현 문제에 취약한 것 같다. 경험 부족이 주 원인이겠지만 이쪽의 사고 흐름이 아직 크게 뚫려있지 않은 것 같다. 11월에는 해당 유형을 많이 풀어봐야겠다.
완전 탐색 가능한 경우 (r,c가 모두 짝수가 아닌 경우)
그리디 알고리즘에 대한 힌트를 얻어도 쉽게 풀이방법을 생각해내기엔 어려웠다. 그렇게 직접 써내려가보면서 약간의 실마리를 풀었다. 부지의 크기가 (홀수 x 홀수), (홀수 x 짝수), (짝수 x 홀수)인 경우는 완전 탐색이 가능하다. 그러므로 탐색 경로만 설계해주면 된다.
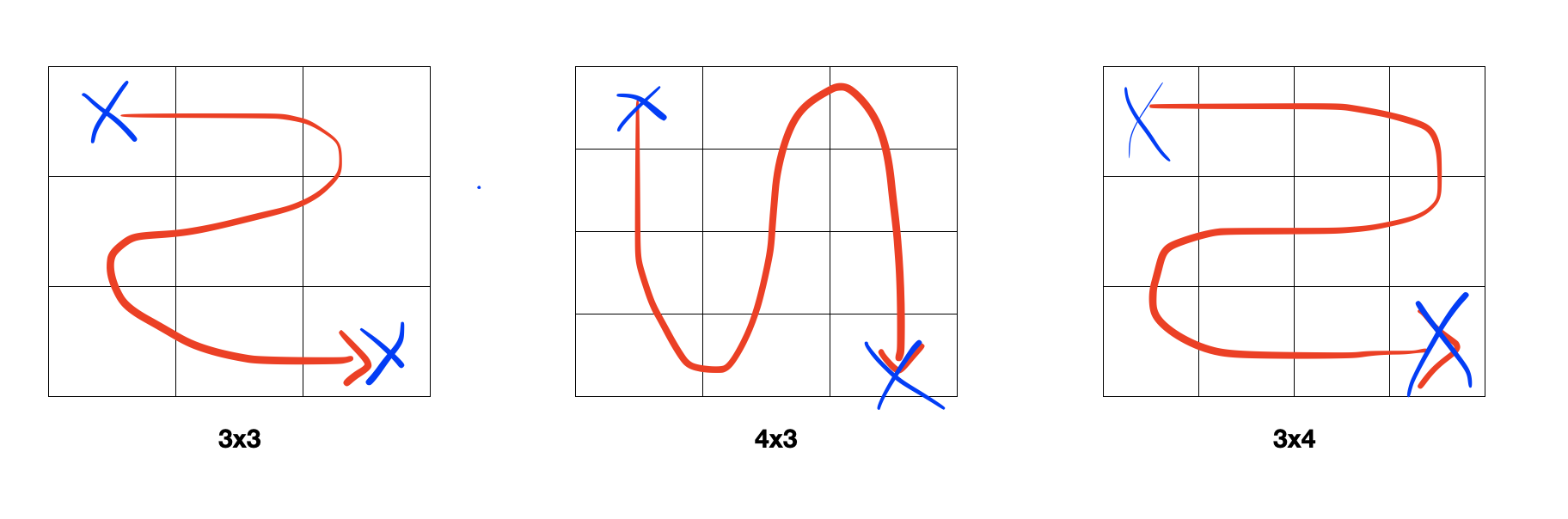
위의 그림을 보면 열(y)의 크기에 따라 탐색 경로가 달라지는 것을 알 수 있다. 홀수인 경우 'ㄹ'자 탐색을 해야 완전 탐색이 가능하고, 짝수인 경우 'N'자 탐색을 해야 완전 탐색이 가능하다.
구현을 하면 다음과 같이 나타낼 수 있다.
public static void main(String[] args) throws IOException{
// 모든 경로 탐색 가능 (x,y가 둘 다 짝수가 아닌 경우)
if(y%2==1) {
// 'ㄹ'자 탐색
sb.append(getZigZag('R','L','D',x,y));
}else {
// 'N'자 탐색
sb.append(getZigZag('D','U','R',y,x));
}
}
static StringBuilder getZigZag(char f, char b, char d, int x, int y) {
StringBuilder sb = new StringBuilder();
for(int i=0; i<y; i++) {
for(int j=0; j<x-1; j++) {
if(i%2==0) {
sb.append(f);
}else {
sb.append(b);
}
}
sb.append(d);
}
return sb;
}
그리디한 탐색이 가능한 경우(r,c가 모두 짝수인 경우)
(짝수 x 짝수)인 부지의 경우 그리디하게 탐색을 해야 하는데 이 부분이 어려웠다. 해당 글을 참고하여 풀이를 진행했다. 부지를 체스판이라고 가정하고 생각해보자. 아래 그림을 보면 시작점(0,0)이 흰색이라고 했을 때, 도착점(x-1, y-1) 또한 무조건 흰색임을 알 수 있다.
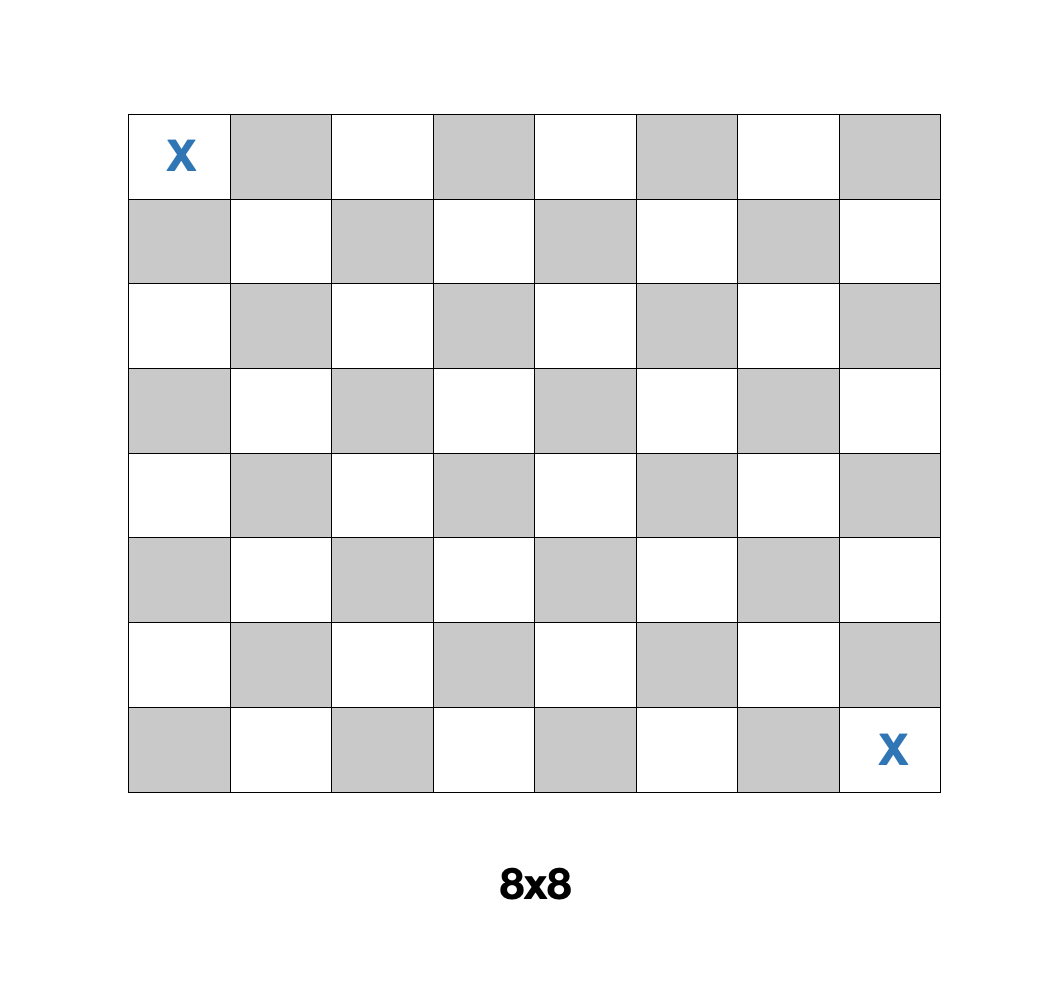
그러면 모든 탐색경로는 [ 흰(출발점) → 검 → 흰 → 검 → .. → 흰 → 검 → 흰(도착점) ] 의 형태로 이루어진다.
- 방문한 칸의 갯수는 흰+1 = 검이다.
- 방문한 칸의 갯수는 흰 > 검이고, 방문하지 않은 칸의 갯수는 흰 < 검이다.
- 따라서, 전체 칸의 갯수는 짝수이고 흰칸과 검은칸의 갯수가 같으므로, 모든 칸을 방문하는 것은 불가능함을 알 수 있다.
그리디하게 탐색하기 위해서는 흰칸 또는 검은칸을 포기해야 한다.
- 흰 칸을 하나 선택하지 않고 그리디하게 탐색할 경우, (흰 <= 검)이게 되는데 이는 도착점에 도달하기 위한 필수조건인 (흰+1 = 검)이 성립하지 않는다. 탐색 자체가 불가능하기 때문에 검은 칸을 추가로 포기해야 한다.
- 검은 칸 하나를 선택하지 않고 그리디하게 탐색할 경우, (흰+1 = 검)이 성립되므로 완전 탐색이 가능하다.
흰 칸을 포기할 경우
여기서 그리디 탐색을 하는데 흰 칸을 하나 방문하지 않는다해도 나머지 칸을 모두 방문하는 것은 불가능하다. 검은 칸 하나 더 포기, 즉 총 2개의 칸을 포기해야 완전 탐색이 가능하다.
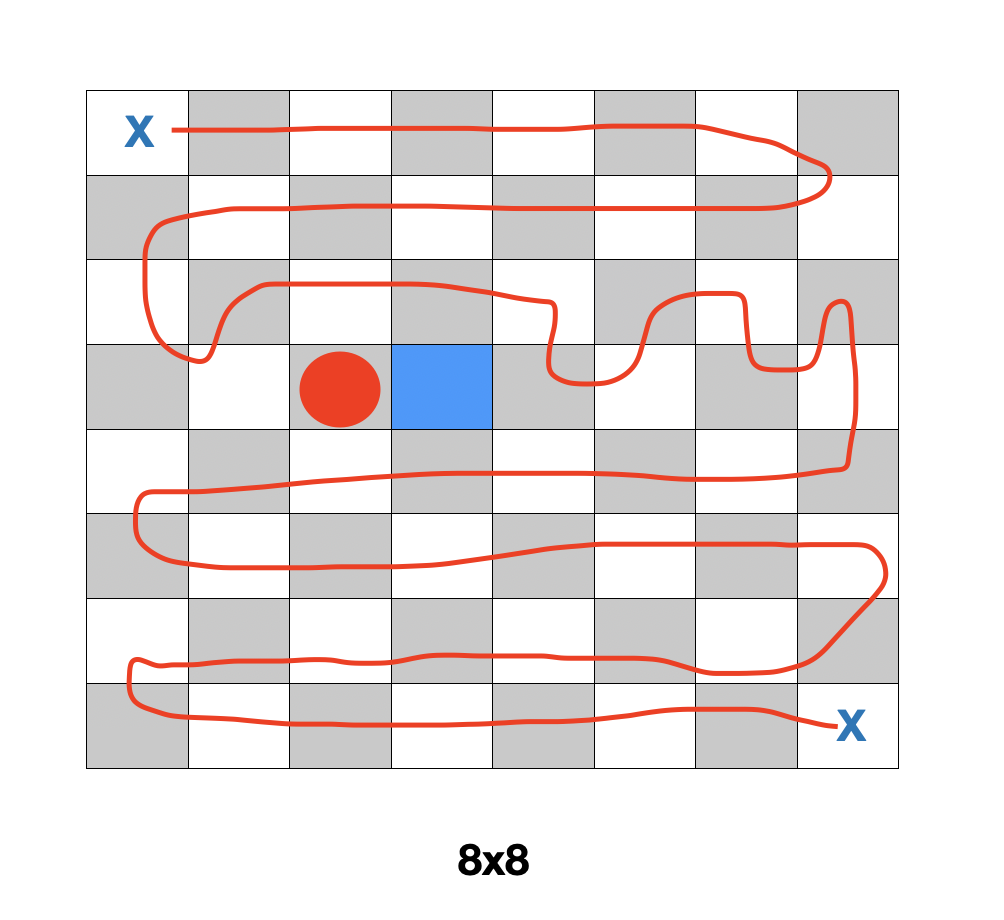
검은 칸을 포기할 경우
반대로, 검은 칸을 하나 방문하지 않는다면 모든 칸을 방문하는 것이 가능해진다.
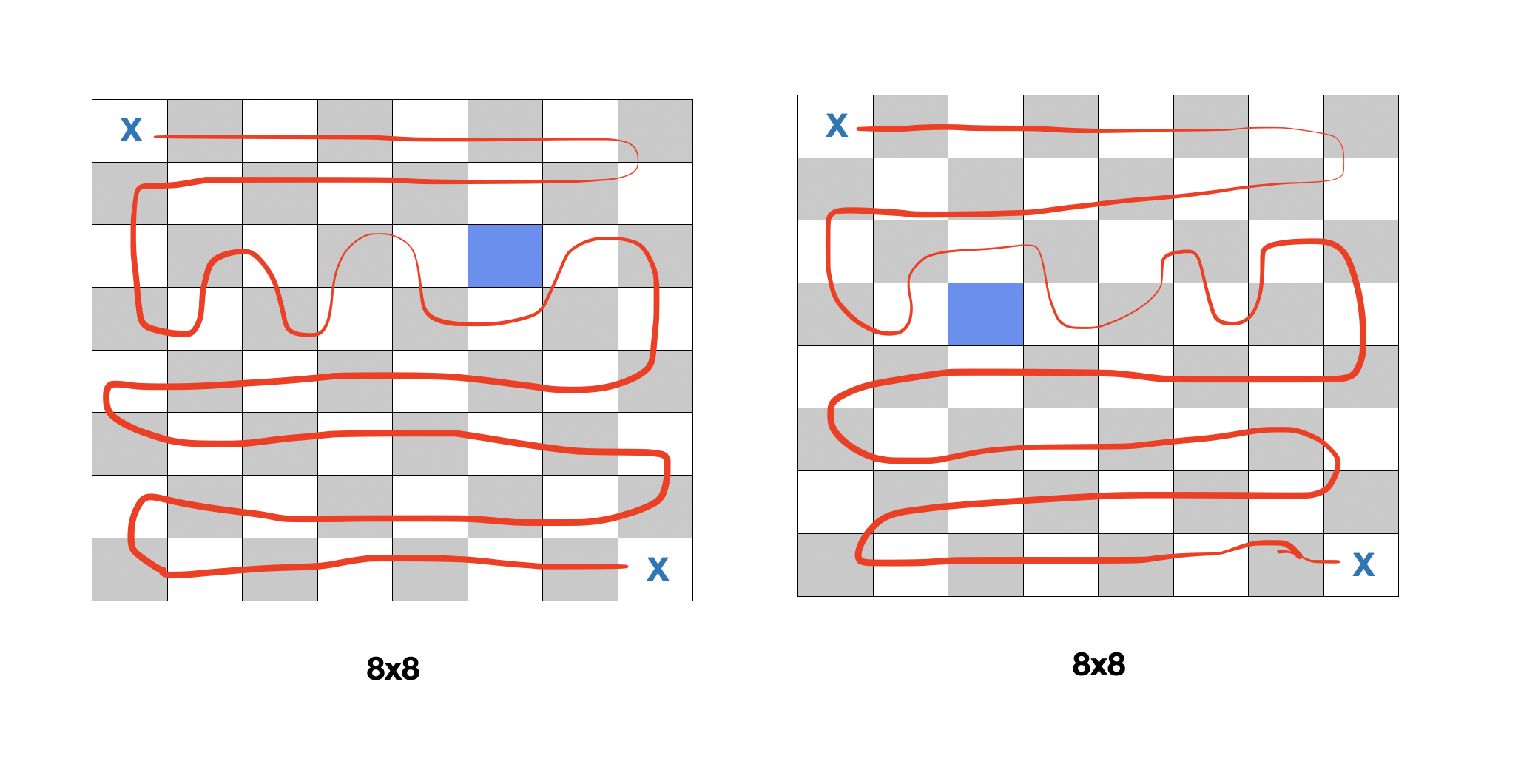
구현
이제 가장 작은 값을 가지는 검은 칸을 고른 후 해당 칸을 제외한 탐색 경로를 뽑아주면 된다. 검은 칸은 (i,j)로 나타냈을 때 항상 홀수 값을 가지므로 최솟값을 구하는 방법은 간단하다.
최솟값을 구하고 위치를 알아냈다면 이제 탐색을 해주면 된다. 다음 그림과 같이 지그재그 탐색 방법은 위의 x,y 모두 짝수가 아닌 경로를 탐색할 때 사용한 방법을 사용하면 된다. 파란상자를 제외하고 윗 부분과 아랫 부분은 다음과 같이 탐색해주면 된다.
- 최솟값 위치의 열(my)가 홀수 인 경우
- 위의 탐색 경로는 바로 윗칸까지 탐색을 해준다. (0~my-1)
- 아래의 탐색경로는 한 칸을 비워두고 탐색을 해준다. (my+2, y)
- 최솟값 위치의 열(my)가 짝수 인 경우
- 위의 탐색 경로는 한 칸을 비워두고 탐색을 해준다. (0~my-2)
- 아래의 탐색경로는 바로 아랫칸까지 탐색을 해준다. (my+1, y)
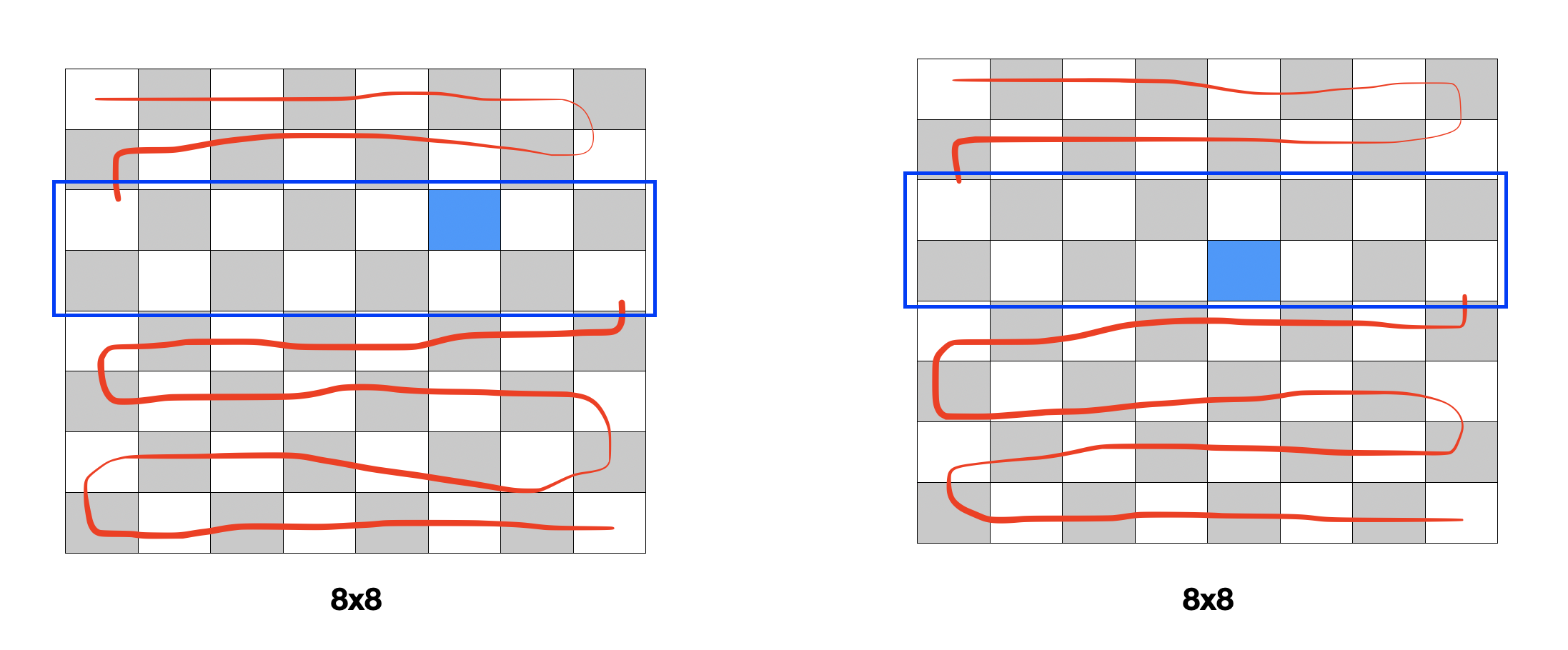
중요한 것은 위의 경로 그린 것을 보면 알겠지만 파란 박스가 있는 구간이다.
- x좌표까지 도달하기 전
- x좌표가 짝수이면, "DR"방향으로 탐색한다.
- x좌표가 홀수이면, "UR"방향으로 탐색한다.
- x좌표에 도달하고 나서
- x좌표가 짝수이면, "RD"방향으로 탐색한다.
- x좌표가 홀수이면, "RU"방향으로 탐색한다.
그림으로 나타내면 다음과 같다. 해당 칸을 건너뜀으로써 경로의 방향이 바뀌는 것을 볼 수 있다.
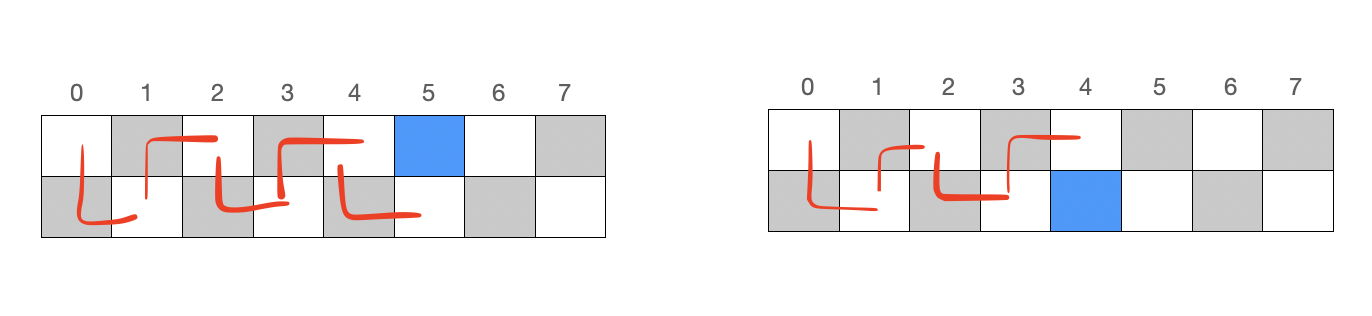
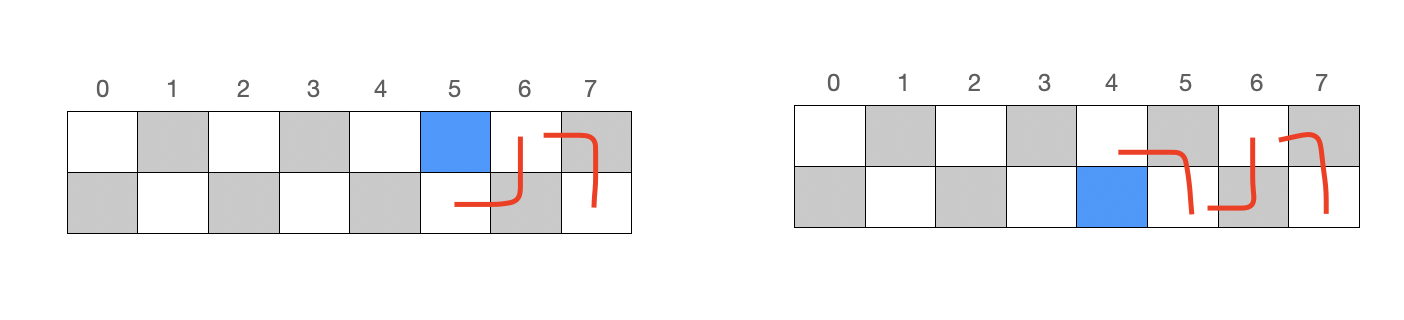
코드로 나타내면 다음과 같다.
for(int i=0; i<ex; i++) {
if(i%2==0) {
sb.append("DR");
}else {
sb.append("UR");
}
}
for(int i=ex; i<x-1; i++) {
if(i%2==0) {
sb.append("RD");
}else {
sb.append("RU");
}
}
풀이 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int y = Integer.parseInt(st.nextToken());
int x = Integer.parseInt(st.nextToken());
StringBuilder sb = new StringBuilder();
// 둘 다 짝수
if((y%2==0) && (x%2==0)) {
// 가장 작은 수 찾기
int minX=0;
int minY=0;
int minV = Integer.MAX_VALUE;
// (0,0) : 흰돌이라 할 때, (i,j) : i+j값이 홀수인 검은 돌 하나 생략 가능
for(int i=0; i<y; i++) {
st = new StringTokenizer(br.readLine());
for(int j=0; j<x; j++) {
if((i+j)%2==1) {
int v = Integer.parseInt(st.nextToken());
if(minV > v) {
minV = v;
minY = i;
minX = j;
}
}else {
st.nextToken();
}
}
}
sb.append(getGreedyZigZag(x, y, minX, minY));
}
else { // 모든 경로 탐색 가능
// 'ㄹ'자 탐색
if(y%2==1) {
sb.append(getZigZag('R','L','D',x,y));
}
// 'N'자 탐색
else {
sb.append(getZigZag('D','U','R',y,x));
}
}
System.out.println(sb.deleteCharAt(sb.length()-1).toString());
}
static StringBuilder getGreedyZigZag(int x, int y, int ex, int ey) {
StringBuilder sb = new StringBuilder();
int uy = ey/2*2;
sb.append(getZigZag('R','L','D',x,uy));
for(int i=0; i<ex; i++) {
if(i%2==0) {
sb.append("DR");
}else {
sb.append("UR");
}
}
for(int i=ex; i<x-1; i++) {
if(i%2==0) {
sb.append("RD");
}else {
sb.append("RU");
}
}
sb.append("D");
sb.append(getZigZag('L' ,'R' ,'D' ,x ,y-uy-2));
return sb;
}
static StringBuilder getZigZag(char f, char b, char d, int x, int y) {
StringBuilder sb = new StringBuilder();
for(int i=0; i<y; i++) {
for(int j=0; j<x-1; j++) {
if(i%2==0) {
sb.append(f);
}else {
sb.append(b);
}
}
sb.append(d);
}
return sb;
}
}
'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 1959번 달팽이3 (Java) (0) | 2021.11.03 |
|---|---|
| [BOJ] 백준 1913번 달팽이 (Java) (0) | 2021.11.02 |
| [BOJ] 백준 13904번 과제 (Java) (0) | 2021.10.31 |
| [BOJ] 백준 10775번 공항 (Java) (0) | 2021.10.30 |
| [BOJ] 백준 9576번 책 나눠주기 (Java) (0) | 2021.10.29 |




