#11주차 아이템 줍기
유형 : 구현 / 그래프 탐색
코딩테스트 연습 - 아이템 줍기
[[1,1,7,4],[3,2,5,5],[4,3,6,9],[2,6,8,8]] 1 3 7 8 17 [[1,1,8,4],[2,2,4,9],[3,6,9,8],[6,3,7,7]] 9 7 6 1 11 [[2,2,5,5],[1,3,6,4],[3,1,4,6]] 1 4 6 3 10
programmers.co.kr
▸ 문제
다음과 같은 다각형 모양 지형에서 캐릭터가 아이템을 줍기 위해 이동하려 합니다.

지형은 각 변이 x축, y축과 평행한 직사각형이 겹쳐진 형태로 표현하며, 캐릭터는 이 다각형의 둘레(굵은 선)를 따라서 이동합니다.
만약 직사각형을 겹친 후 다음과 같이 중앙에 빈 공간이 생기는 경우, 다각형의 가장 바깥쪽 테두리가 캐릭터의 이동 경로가 됩니다.
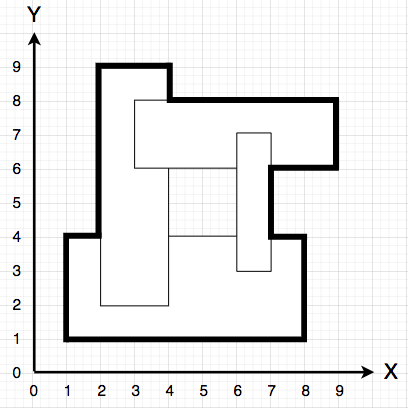
단, 서로 다른 두 직사각형의 x축 좌표 또는 y축 좌표가 같은 경우는 없습니다.

즉, 위 그림처럼 서로 다른 두 직사각형이 꼭짓점에서 만나거나, 변이 겹치는 경우 등은 없습니다.
다음 그림과 같이 지형이 2개 이상으로 분리된 경우도 없습니다.
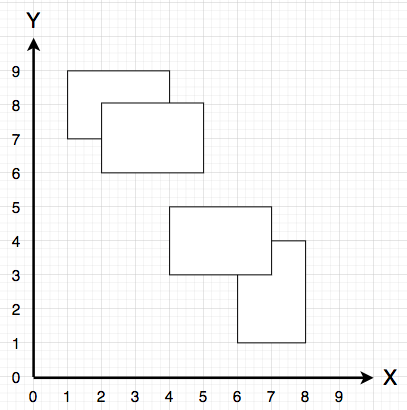
한 직사각형이 다른 직사각형 안에 완전히 포함되는 경우 또한 없습니다.

지형을 나타내는 직사각형이 담긴 2차원 배열 rectangle, 초기 캐릭터의 위치 characterX, characterY, 아이템의 위치 itemX, itemY가 solution 함수의 매개변수로 주어질 때, 캐릭터가 아이템을 줍기 위해 이동해야 하는 가장 짧은 거리를 return 하도록 solution 함수를 완성해주세요.
▸ 제한사항
- rectangle의 세로(행) 길이는 1 이상 4 이하입니다.
- rectangle의 원소는 각 직사각형의 [좌측 하단 x, 좌측 하단 y, 우측 상단 x, 우측 상단 y] 좌표 형태입니다.
- 직사각형을 나타내는 모든 좌표값은 1 이상 50 이하인 자연수입니다.
- 서로 다른 두 직사각형의 x축 좌표, 혹은 y축 좌표가 같은 경우는 없습니다.
- 문제에 주어진 조건에 맞는 직사각형만 입력으로 주어집니다.
- charcterX, charcterY는 1 이상 50 이하인 자연수입니다.
- 지형을 나타내는 다각형 테두리 위의 한 점이 주어집니다.
- itemX, itemY는 1 이상 50 이하인 자연수입니다.
- 지형을 나타내는 다각형 테두리 위의 한 점이 주어집니다.
- 캐릭터와 아이템의 처음 위치가 같은 경우는 없습니다.
문제 풀이
그래프 탐색 구현 문제로 꽤나 어려웠다. 이 글을 참고하여 풀이를 끝까지 진행할 수 있었다. 구현은 어떻게 보면 기존에 정립된 알고리즘을 적용하는 것이 아닌 문제를 있는 그대로 규칙을 찾아 풀이를 하는 것이기 때문에 알고리즘 사고 능력을 제대로 측정할 수 있는 유형 중 하나가 아닐까 싶다.
- 맵 크기를 2배로 확장한 다음 맵 바운더리 BFS탐색하기
- 맵에 상,하,좌,우를 기록한 다음 모든 조건분기별로 나눠서 방향 탐색하기
맵 크기 2배로 확장하기
나는 1번 방식을 선택하여 풀이를 하였다. 별 이유는 없고 구현하기 더 쉬운 방법이었기 때문이다. 맵을 2배로 확장하는 이유는 맵 탐색을 하는데 선이 아닌 좌표를 기준으로 하기 때문에 (1,0) (1,1)이 바로 연결되어 있는 것인지 아니면 다른 경로로 연결되어 있는 것인지 판단하기 어렵기 때문에 제대로 된 탐색을 할 수 없기 때문이다.

다음과 같이 맵 크기를 2배로 확장하면 제대로 된 경로 탐색을 할 수가 있다. 좌표를 더 잘게 쪼갤 수 없기 때문에 맵을 늘려주는 방식을 택한 것이다.

BFS 최단거리 탐색
경로 탐색의 문제를 해결하면 결국 최단거리를 구하는 문제가 된다. 이는 BFS탐색으로 해결하면 된다. 경로는 총 2가지인데 BFS탐색을 해서 먼저 도착하는 경로가 최단 경로가 되기 때문이다.

설계
- 주어진 사각형의 좌표를 2배로 크게만든 다음 list와 이차원 배열 맵에 -1로 표시해준다.
- sx *= 2, sy *= 2;
- ex *= 2, ey *= 2;
- BFS 탐색을 통해 출발점에서 목적 지점으로 가는 최단 경로를 찾는다. bfs(map, characterX*2, characterY*2, itemX*2, itemY*2);
- 입력된 사각형의 바운더리만 이동이 가능하게 조건을 설정한다.
- 목적지점(tx, ty)에 도착했으면 기존에 맵을 2배로 늘렸기 때문에 2로 나눠준 값을 출력한다. return (move/2);
풀이 코드
import java.util.*;
class Solution {
static class Rect{
int x1,x2,y1,y2;
public Rect(int x1, int y1, int x2, int y2) {
this.x1 =x1;
this.y1 =y1;
this.x2 =x2;
this.y2 =y2;
}
}
static int x,y;
static List<Rect> rectList;
static int[] dx = {-1, 1, 0, 0};
static int[] dy = {0, 0, -1, 1};
public int solution(int[][] rectangle, int characterX, int characterY, int itemX, int itemY) {
int answer = 0;
int[][] map = new int[102][102];
rectList = new ArrayList<>();
for(int i=0; i<rectangle.length; i++) {
int sx = rectangle[i][0]*2;
int sy = rectangle[i][1]*2;
int ex = rectangle[i][2]*2;
int ey = rectangle[i][3]*2;
for(int y=sy; y<=ey; y++) {
for(int x=sx; x<=ex; x++) {
map[y][x] = -1;
}
}
rectList.add(new Rect(sx,sy,ex,ey));
}
answer= bfs(map, characterX*2, characterY*2, itemX*2, itemY*2);
return answer;
}
static int bfs(int[][] map, int x, int y, int tx, int ty) {
Queue<int[]> q = new LinkedList<>();
q.add(new int[] {x, y, 1});
map[y][x] = 1;
while(!q.isEmpty()) {
int[] p = q.poll();
int px = p[0];
int py = p[1];
int move = p[2];
if(px == tx && py == ty) {
return (move/2);
}
for(int i=0; i<4; i++) {
int nx = px + dx[i];
int ny = py + dy[i];
if(map[ny][nx] < 0 && isBoundary(nx,ny)) {
map[ny][nx] = move+1;
q.add(new int[] {nx, ny, move+1});
}
}
}
return -1;
}
static boolean isBoundary(int x, int y) {
for(Rect r : rectList) {
if(r.x1 < x && r.y1 <y && r.x2 > x && r.y2 > y) return false;
}
return true;
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [프로그래머스] 위클리 챌린지 12주차 피로도 (Java) (0) | 2021.11.07 |
|---|---|
| [BOJ] 백준 14891번 톱니바퀴 (Java) (0) | 2021.11.06 |
| [BOJ] 백준 5430번 AC (Java) (0) | 2021.11.04 |
| [BOJ] 백준 1959번 달팽이3 (Java) (0) | 2021.11.03 |
| [BOJ] 백준 1913번 달팽이 (Java) (0) | 2021.11.02 |




