#12767 Ceiling Function
난이도 : 골드 1
유형 : 트리 / BST
12767번: Ceiling Function
Advanced Ceiling Manufacturers (ACM) is analyzing the properties of its new series of Incredibly Collapse-Proof Ceilings (ICPCs). An ICPC consists of n layers of material, each with a different value of collapse resistance (measured as a positive integer).
www.acmicpc.net
▸ 문제
Advanced Ceiling Manufacturers (ACM) is analyzing the properties of its new series of Incredibly Collapse-Proof Ceilings (ICPCs). An ICPC consists of n layers of material, each with a different value of collapse resistance (measured as a positive integer). The analysis ACM wants to run will take the collapse-resistance values of the layers, store them in a binary search tree, and check whether the shape of this tree in any way correlates with the quality of the whole construction. Because, well, why should it not?
To be precise, ACM takes the collapse-resistance values for the layers, ordered from the top layer to the bottom layer, and inserts them one-by-one into a tree. The rules for inserting a value v are:
- If the tree is empty, make v the root of the tree.
- If the tree is not empty, compare v with the root of the tree. If v is smaller, insert v into the left subtree of the root, otherwise insert v into the right subtree.
ACM has a set of ceiling prototypes it wants to analyze by trying to collapse them. It wants to take each group of ceiling prototypes that have trees of the same shape and analyze them together.
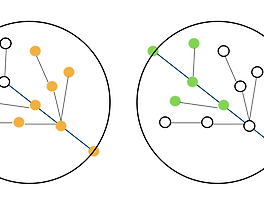
For example, assume ACM is considering five ceiling prototypes with three layers each, as described by Sample Input 1 and shown in Figure C.1. Notice that the first prototype’s top layer has collapseresistance value 2, the middle layer has value 7, and the bottom layer has value 1. The second prototype has layers with collapse-resistance values of 3, 1, and 4 – and yet these two prototypes induce the same tree shape, so ACM will analyze them together.
Given a set of prototypes, your task is to determine how many different tree shapes they induce.
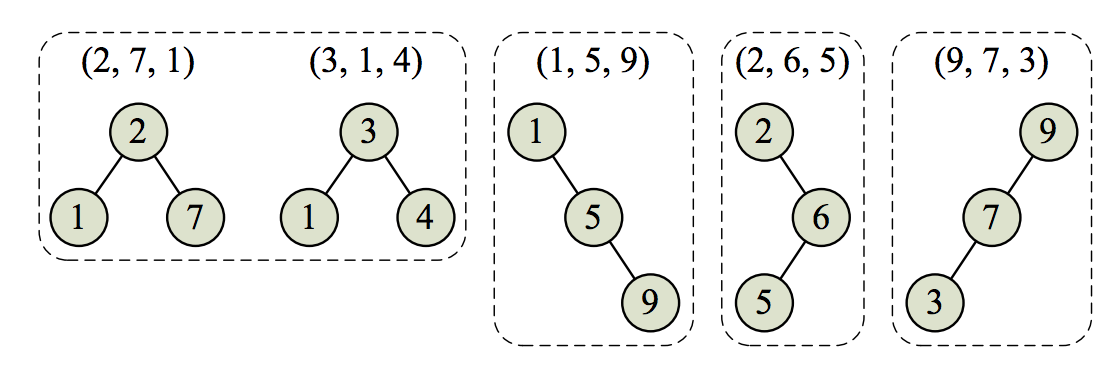
Figure C.1: The four tree shapes induced by the ceiling prototypes in Sample Input 1.
▸ 입력
The first line of the input contains two integers n (1 ≤ n ≤ 50), which is the number of ceiling prototypes to analyze, and k (1 ≤ k ≤ 20), which is the number of layers in each of the prototypes.
The next n lines describe the ceiling prototypes. Each of these lines contains k distinct integers (between 1 and 106, inclusive), which are the collapse-resistance values of the layers in a ceiling prototype, ordered from top to bottom.
▸ 출력
Display the number of different tree shapes.
문제 풀이
주어진 입력 데이터를 이진 검색 트리로 만들어준 다음 형태의 갯수를 출력해주면 됩니다. 이진 검색 트리의 특징은 다음과 같습니다.
- 노드의 왼쪽 하위 트리에는 노드의 data보다 작은 data가 포함되어 있는 노드만 포함된다.
- 노드의 오른쪽 하위 트리에는 노드의 data보다 큰 data가 포함되어 있는 노드만 포함된다.
- 중복된 키는 허용되지 않는다.
그래서 일단 왼쪽, 오른쪽 자식 트리를 가지고 자신의 data를 보유한 단순 Node의 형태를 다음과 같이 구현해주면 됩니다.
static class Node{
int data;
Node left;
Node right;
Node(int data){
this.data = data;
this.left = null;
this.right = null;
}
}
그런 다음 해당 Node를 가지고 BST를 구현하는 클래스를 정의해줍니다. 여기서 기존의 BST와는 다른 점이 있습니다. 문제에서는 같은 형태의 이진검색 트리를 판별해야 됩니다.
- 그래서 각 노드의 번호를 저장하는 List 자료구조와 각 노드의 idx를 계산해주는 로컬 변수를 추가해줬습니다.
- 그리고 내부 구현 함수로는 insert(int num)만 구현해줬습니다.
- root == null이면, root를 생성해주고 idx = 1을 저장해준다.
- cur.data > num 이면, 왼쪽 하위 트리로 이동하고 idx = idx*2로 증가시켜준다.
- cur.data < num 이면, 오른쪽 하위 트리로 이동하고 idx = idx*2 +1로 증가시켜준다.
static class BinarySearchTree{
Node root;
List<Integer> shape = new ArrayList<>();
int idx;
void insert(int num) {
Node insert = new Node(num);
idx = 1;
if(root == null) {
root = insert;
shape.add(idx);
return;
}
Node cur = root, pa = null;
while(true) {
pa = cur;
if(cur.data > num) {
cur = cur.left;
idx = idx*2;
if(cur == null) {
pa.left = insert;
shape.add(idx);
return;
}
}else {
cur = cur.right;
idx = idx*2+1;
if(cur == null) {
pa.right = insert;
shape.add(idx);
return;
}
}
}
}
}
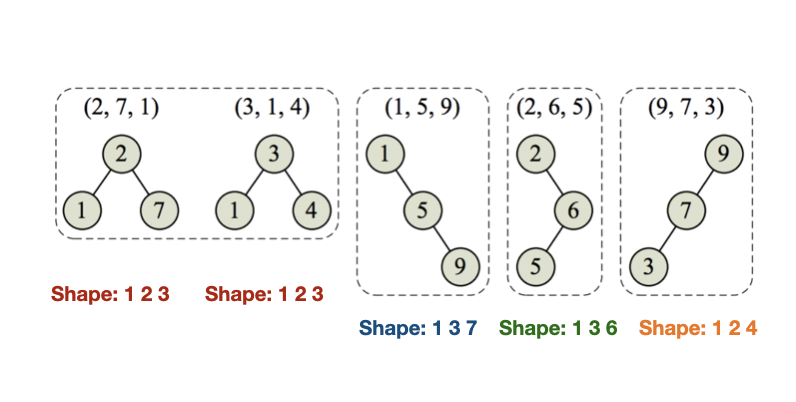
그러면 각 BST 형태를 다음과 같이 각 노드의 위치를 담은 idx 리스트로 표현할 수 있습니다. 이를 이젠 Set 자료구조에 담아 갯수를 세어주면 됩니다.
설계
- 주어진 n개의 트리 데이터로 BST를 만들어준다.
- tree.insert(num);
- 그렇게 나온 각 BST 형태를 Set 자료구조에 저장한다.
- set.add(sb.toString());
- Set에 저장된 형태의 갯수를 출력해준다.
- System.out.println(set.size());
풀이 코드
import java.io.*;
import java.util.*;
public class Main {
static class Node{
int data;
Node left;
Node right;
Node(int data){
this.data = data;
this.left = null;
this.right = null;
}
}
static class BinarySearchTree{
Node root;
List<Integer> shape = new ArrayList<>();
int idx;
void insert(int num) {
Node insert = new Node(num);
idx = 1;
if(root == null) {
root = insert;
shape.add(idx);
return;
}
Node cur = root, pa = null;
while(true) {
pa = cur;
if(cur.data > num) {
cur = cur.left;
idx = idx*2;
if(cur == null) {
pa.left = insert;
shape.add(idx);
return;
}
}else {
cur = cur.right;
idx = idx*2+1;
if(cur == null) {
pa.right = insert;
shape.add(idx);
return;
}
}
}
}
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
Set<String> set = new HashSet<>();
for(int i=0; i<n; i++) {
BinarySearchTree tree = new BinarySearchTree();
st = new StringTokenizer(br.readLine());
for(int j=0; j<k; j++) {
int num = Integer.parseInt(st.nextToken());
tree.insert(num);
}
Collections.sort(tree.shape);
StringBuilder sb = new StringBuilder();
for(int num : tree.shape) {
sb.append(num);
}
set.add(sb.toString());
}
System.out.println(set.size());
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 17299번 오등큰수 (Java) (0) | 2021.12.18 |
|---|---|
| [BOJ] 백준 2132번 나무 위의 벌레 (Java) (0) | 2021.12.17 |
| [BOJ] 백준 4179번 불! (Java) (1) | 2021.12.15 |
| [BOJ] 백준 13244번 Tree (Java) (0) | 2021.12.14 |
| [BOJ] 백준 6597번 트리 복구 (Java) (0) | 2021.12.13 |