#11376 열혈강호 2
난이도 : 플레 4
유형 : 이분 매칭
11376번: 열혈강호 2
강호네 회사에는 직원이 N명이 있고, 해야할 일이 M개가 있다. 직원은 1번부터 N번까지 번호가 매겨져 있고, 일은 1번부터 M번까지 번호가 매겨져 있다. 각 직원은 최대 두 개의 일을 할 수 있고,
www.acmicpc.net
▸ 문제
강호네 회사에는 직원이 N명이 있고, 해야할 일이 M개가 있다. 직원은 1번부터 N번까지 번호가 매겨져 있고, 일은 1번부터 M번까지 번호가 매겨져 있다.
각 직원은 최대 두 개의 일을 할 수 있고, 각각의 일을 담당하는 사람은 1명이어야 한다.
각각의 직원이 할 수 있는 일의 목록이 주어졌을 때, M개의 일 중에서 최대 몇 개를 할 수 있는지 구하는 프로그램을 작성하시오.
▸ 입력
첫째 줄에 직원의 수 N과 일의 개수 M이 주어진다. (1 ≤ N, M ≤ 1,000)
둘째 줄부터 N개의 줄의 i번째 줄에는 i번 직원이 할 수 있는 일의 개수와 할 수 있는 일의 번호가 주어진다.
▸ 출력
첫째 줄에 강호네 회사에서 할 수 있는 일의 개수를 출력한다.
문제 풀이
백준 11375번 열혈강호의 문제와 거의 동일하다. 추가된 부분은 직원이 두 가지 일을 할 수 있다는 것이다. 그러면 방법은 간단하다. 각 직원들을에게 일 매칭을 2번씩 해주면 된다.
시뮬레이션
이분 매칭 구현은 포드-폴커슨 알고리즘처럼 증가 경로를 찾은 뒤 유량을 보내는 것을 반복해주면 된다. 문제에서 주어진 예제를 통해 시뮬레이션을 돌려보자.
1번 직원 일 배정하기
- 1번 직원은 (a, b)에 매칭이 가능하므로, a, b에 모두 매칭한다.
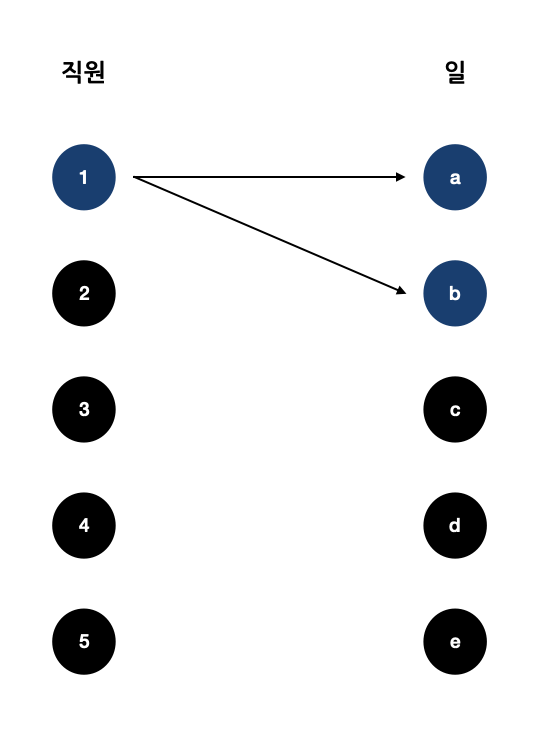
2번 직원 일 배정하기
- 2번 직원은 (a, b)에 매칭이 가능한데, 이미 1번 직원이 모두 점유하고 있으므로 일 배정이 불가능하다.
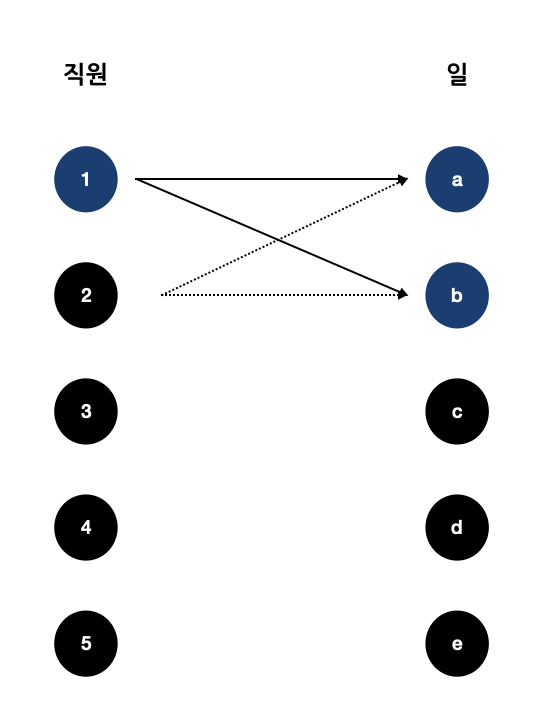
3번 직원 일 배정하기
- 3번 직원 또한 (a, b)에 매칭이 가능한데, 이미 1번 직원이 모두 점유하고 있으므로 일 배정이 불가능하다.

4번 직원 일 배정하기
- 4번 직원은 (d, e)에 매칭이 가능하므로, d, e에 모두 매칭한다.
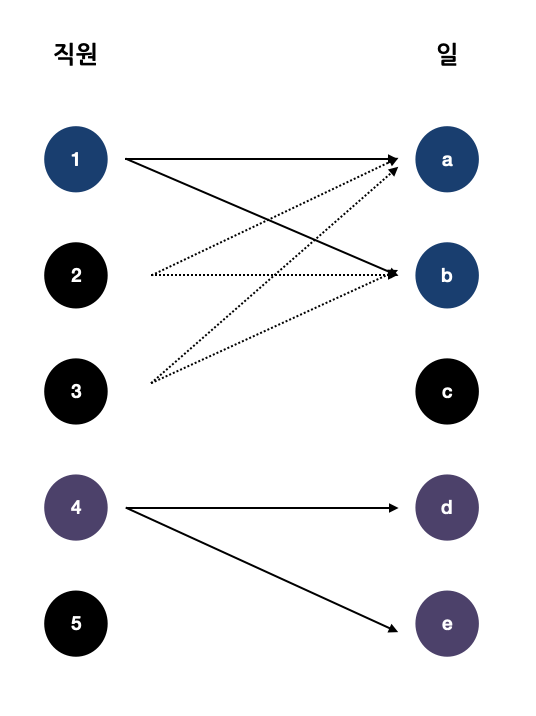
5번 직원 일 배정하기
- 5번 직원은 맡을 수 있는 일이 없으므로 이대로 일 배정을 종료한다.
따라서, 총 최대로 4개의 일을 배정할 수 있음을 알 수 있다.
이분매칭에 대한 자세한 내용은 여기를 참고해주세요.
풀이 코드
import java.io.*;
import java.util.*;
public class Main {
static List<Integer>[] list;
static int[] task;
static boolean[] check;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
list = new ArrayList[n+1];
for(int i=1; i<=n; i++) {
list[i] = new ArrayList<>();
}
task = new int[m+1];
check = new boolean[m+1];
for(int i=1; i<=n; i++) {
st = new StringTokenizer(br.readLine());
int nn = Integer.parseInt(st.nextToken());
for(int j=0; j<nn; j++) {
list[i].add(Integer.parseInt(st.nextToken()));
}
}
int cnt = 0;
for(int i=1; i<=n; i++) {
for(int j=0; j<2; j++) {
Arrays.fill(check, false);
if(dfs(i)) cnt++;
}
}
System.out.println(cnt);
}
static boolean dfs(int here) {
for(int nxt : list[here]) {
if(check[nxt]) continue;
check[nxt] = true;
if(task[nxt] == 0 || dfs(task[nxt])) {
task[nxt] = here;
return true;
}
}
return false;
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 16975번 수열과 쿼리 21 (Java) - Fenwick (0) | 2022.01.04 |
|---|---|
| [BOJ] 백준 11377번 열혈강호 3 (Java) (0) | 2022.01.03 |
| [BOJ] 백준 11375번 열혈강호 (Java) (0) | 2022.01.01 |
| [BOJ] 백준 2188번 축사 배정 (Java) (0) | 2021.12.31 |
| [BOJ] 백준 13397번 구간 나누기 2 (Java) (0) | 2021.12.30 |




