#5419 북서풍
난이도 : 플레 4
유형 : 세그먼트 트리 / 좌표 압축
5419번: 북서풍
각 테스트 케이스에 대해서, 북서풍을 타고 항해할 수 있는 섬의 쌍의 수를 출력한다.
www.acmicpc.net
▸ 문제
강한 북서풍이 불고 있다. 이 뜻은 동쪽과 남쪽 사이의 모든 방향으로 항해할 수 있다는 뜻이다. 북쪽이나 서쪽으로 항해하는 것은 불가능하다.
작은 섬이 여러 개 있는 바다가 있다. 섬은 좌표 평면의 한 점으로 나타낼 수 있다. y 좌표가 증가하는 방향은 북쪽, x좌표가 증가하는 방향은 동쪽이다. 북서풍을 타고 항해할 수 있는 섬의 쌍의 수를 구하는 프로그램을 작성하시오.
▸ 입력
첫째 줄에 테스트 케이스의 개수가 주어진다.
각 테스트 케이스의 첫째 줄에는 섬의 수 n (1 ≤ n ≤ 75000)이 주어진다. 다음 n개 줄에는 각 섬의 좌표 xi, yi가 주어진다. 두 섬의 좌표가 같은 경우는 없다. (-109 ≤ xi, yi ≤ 109)
▸ 출력
각 테스트 케이스에 대해서, 북서풍을 타고 항해할 수 있는 섬의 쌍의 수를 출력한다.
문제 풀이
문제는 일단 세그먼트 트리이다. 좌표를 압축하여 자신보다 앞(북서쪽)에 위치한 섬들을 카운트해주면 된다. x, y를 완전탐색하면 O(n^2)이기 떄문에 트리 구조를 사용하여 로그함수대로 시간을 줄여주는 것이다.
먼저 좌표를 그려보면서 북서풍을 타고 항해할 수 있는 섬이 어떻게 되는지 살펴보자.

다음과 같이 북서풍으로 탐색한다는 것은 y축이 더 크거나 x축이 작은 곳을 탐색한다는 것과 같다는 것을 알 수 있다. 그러므로 이제 섬들을 1차원 좌표로 압축시켜 우선순위대로 자신의 앞(북서풍)에 몇 개의 섬이 위치했는지 카운트해주는 문제로 바꿔주면 된다.
y좌표 압축하기
1차원으로 압축시켜야 하기 때문에 그 기준이 x나 y좌표 어떤 것이 되어도 상관없다. 1번의 예제로 y축을 압축시킨다고 했을 때 시뮬레이션을 돌려보면 (-10, -10), (-10, 10), (10, -10), (10, 10)이라는 세 개의 섬이 있을 때 (-10, 2), (-10, 1), (10, 2), (10, 1)로 변한다.
- 어떻게 좌표를 압축시켜도 상관없다. 오름차순 내림차순. 트리에 어떻게 저장하고 어떻게 쿼리를 꺼낼지 그에따라 맞춰주기만 하면 된다. 나는 y축이 클수록 작은 인덱스를 부여했다. y=10은 1로, -10은 2로 압축했다.
x좌표 오름차순 정렬
그런 다음 x축을 오름차순으로 정렬해준다. 왜냐하면 서쪽에 있을수록(x값이 작을수록) 우선순위가 더 높기 때문이다. 그러면 세그먼트 트리에 (-10,1) → (-10,2) → (10,1) → (10,2)로 저장해준다.
세그먼트 트리에 값 저장 및 카운팅
1. (-10, 1)의 좌표 삽입
- 원래 좌표는 (-10, 10)이다. 가장 앞의 인덱스에 저장된다.
- 자신보다 앞에 있는 좌표는 없으므로 0이 카운팅된다.
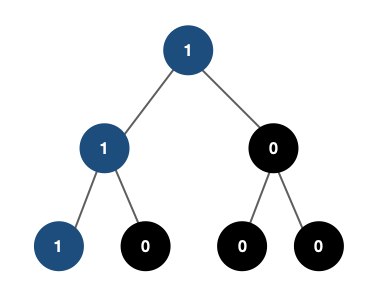
1. (-10, 2)의 좌표 삽입
- 원래 좌표는 (-10, -10)이다. 두 번째 인덱스에 저장된다.
- 자신보다 앞에 있는 좌표는 1개 있으므로 1이 카운팅 된다

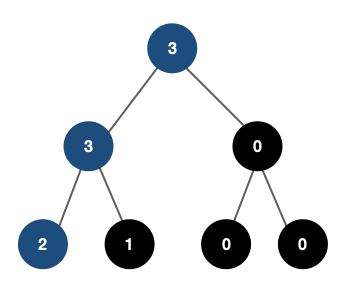
1. (10, 1)의 좌표 삽입
- 원래 좌표는 (10, 10)이다. 첫 번째 인덱스에 저장된다.
- 좌표를 삽입하기 전 자신보다 앞에 있는 좌표는 1개(-10,1) 있으므로 1이 카운팅 된다. 이것이 x좌표를 오름차순한 이유이다.
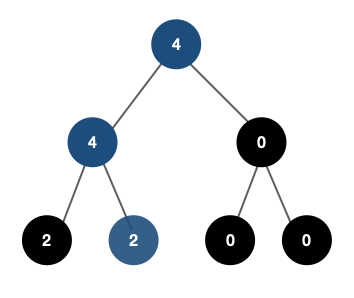
1. (10, 2)의 좌표 삽입
- 원래 좌표는 (10, -10)이다. 두 번째 인덱스에 저장된다.
- 좌표를 삽입하기 전 자신보다 앞에 있는 좌표는 3개 전부이므로 3이 카운팅된다.
풀이 코드
import java.io.*;
import java.util.*;
public class Main {
static class Point{
int x, y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
static int[] tree;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine());
StringTokenizer st;
while(t-->0){
int n = Integer.parseInt(br.readLine());
List<Point> p = new ArrayList<>();
for(int i=0; i<n; i++) {
st = new StringTokenizer(br.readLine());
p.add(new Point(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken())));
}
Collections.sort(p, (a,b) -> b.y-a.y);
int[] tmp = new int[n];
int cnt =1;
for(int i=0; i<n; i++) {
if(i>0 && p.get(i).y != p.get(i-1).y) cnt++;
tmp[i] = cnt;
}
for(int i=0; i<n; i++) {
p.get(i).y = tmp[i];
}
Collections.sort(p, (a,b) -> {
if(a.x == b.x) return a.y - b.y;
else return a.x-b.x;
});
tree = new int[4*n];
long res = 0;
for(int i=0; i<n; i++) {
res += query(1, n, 1, 1, p.get(i).y);
update(1, n, 1, p.get(i).y);
}
System.out.println(res);
}
}
static void update(int s, int e, int node, int idx) {
if(idx < s || e < idx) return;
tree[node] += 1;
if(s == e) return;
int mid = (s+e)/2;
update(s, mid, node*2, idx);
update(mid+1, e, node*2+1, idx);
}
static int query(int s, int e, int node, int l ,int r) {
if(e < l || r < s) return 0;
if(l <= s && e <= r) return tree[node];
int mid = (s+e)/2;
return query(s, mid, node*2, l, r) + query(mid+1, e, node*2+1, l, r);
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 12846번 무서운 아르바이트 (Java) (0) | 2022.02.01 |
|---|---|
| [BOJ] 백준 1615번 교차개수세기 (Java) (0) | 2022.01.31 |
| [BOJ] 백준 1849번 순열 (Java) (0) | 2022.01.29 |
| [BOJ] 백준 1572번 중앙값 (Java) (0) | 2022.01.28 |
| [BOJ] 백준 1671번 상어의 저녁식사 (Java) (0) | 2022.01.27 |




