#10090 Counting Inversions
난이도 : 플레 5
유형 : 세그먼트 트리
10090번: Counting Inversions
A permutation of integers from 1 to n is a sequence a1, a2, ..., an, such that each integer from 1 to n is appeared in the sequence exactly once. Two integers in а permutation form an inversion, when the bigger one is before the smaller one. As an example
www.acmicpc.net
▸ 문제
A permutation of integers from 1 to n is a sequence a1, a2, ..., an, such that each integer from 1 to n is appeared in the sequence exactly once.
Two integers in а permutation form an inversion, when the bigger one is before the smaller one.
As an example, in the permutation 4 2 7 1 5 6 3, there are 10 inversions in total. They are the following pairs: 4–2, 4–1, 4–3, 2–1, 7–1, 7–5, 7–6, 7–3, 5–3, 6–3.
Write program invcnt that computes the number of the inversions in a given permutation.
▸ 입력
The value for the number n is written on the first line of the standard input. The permutation is written on the second line: n numbers, delimited by spaces.
- 2 ≤ n ≤ 1000000
▸ 출력
Write the count of inversions on the standard output.
문제 풀이
자신보다 앞에 있는 수들 중 자신보다 작은 값의 개수를 카운팅해주는 문제이다. n의 최대는 100만이기 때문에 선형탐색으로 하면 시간초과가 발생한다. 그래서 분할정복아니면 세그먼트 트리 자료구조를 이용하여 O(nlogn)의 시간복잡도까지 줄여줘야 한다.
4 2 7 1 5 6 3을 차례대로 인덱스 트리에 넣어 자신보다 앞에 자신보다 작은 값의 개수를 구하면 된다.
- 4는 1, ,2, 3이 아직 트리에 입력되지 않았으므로 카운트 3, 2는 1이 아직 트리에 입력되지 않았으므로 카운트 1 ... 이런식으로 해주면 된다.
- 그럼 쿼리는 값 x라 할 때, (x-1)의 수들 중 현재 인덱스 트리에 들어있는 수(query(1~x-1))를 빼주면 된다.
- int res = (x-1) + query(1~x-1)이다.
그럼 입력을 반대로 넣어주면 간단하게 query(1~x-1)로만도 Inversion Counting 값을 구할 수 있다. 이미 들어있는 수들 중에 자신보다 작은 값을 찾아주면 되기 때문이다.
3 입력
- 3 입력 → query(1, 2) 자신보다 앞에 3보다 작은 수가 입력된 것이 없으므로 0
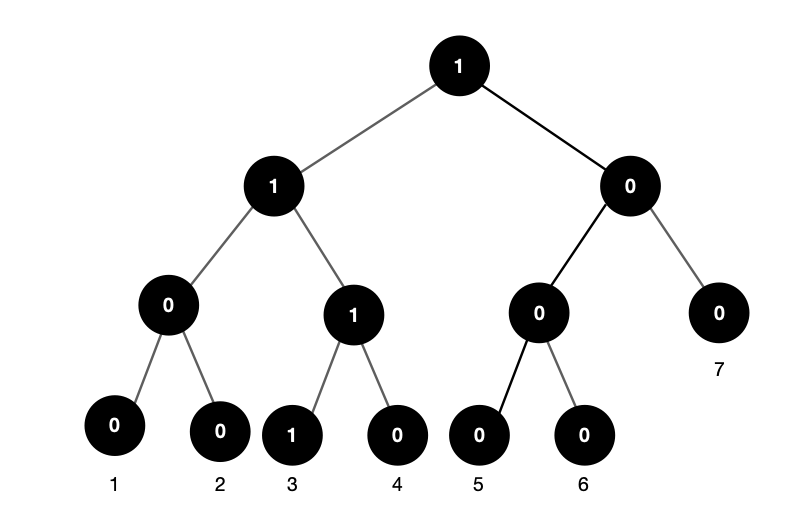
3 입력
- 6 입력 → query(1, 5) 자신보다 앞에 6보다 작은 수가 3 있으므로 1 카운팅
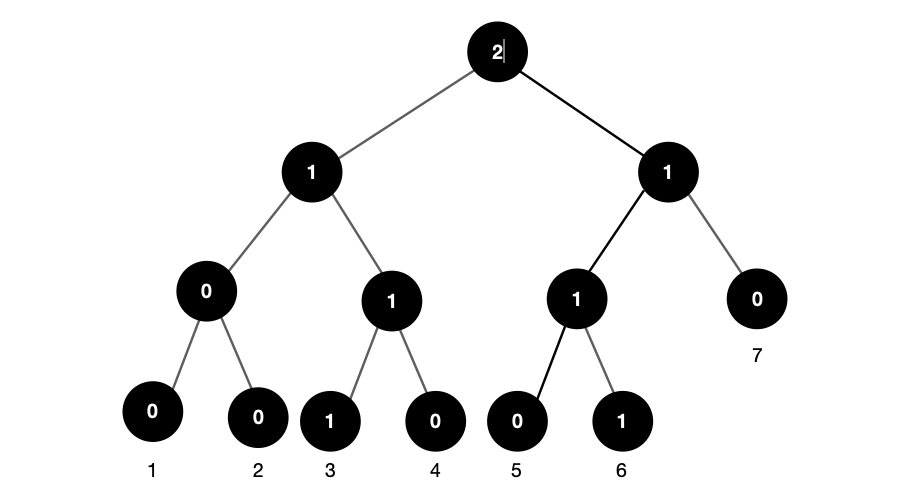
이렇게 구한 수를 모두 더해 출력해주면 된다.
풀이 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int[] tree;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine());
int[] arr = new int[n+1];
for(int i=1; i<=n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
tree = new int[n*4];
long res = 0;
for(int i=n; i>0; i--) {
int x = arr[i];
res += query(1, n, 1, 1, x-1);
update(1, n, 1, x);
}
System.out.println(res);
}
static int update(int s, int e, int node, int idx) {
if(e < idx || idx < s) return tree[node];
if(s == e) return tree[node] +=1 ;
int mid = (s+e)/2;
return tree[node] = update(s, mid, node*2, idx) + update(mid+1, e, node*2+1, idx);
}
static int query(int s, int e, int node, int l, int r) {
if(r < s || e < l) return 0;
if(l <= s && e <= r)return tree[node];
int mid = (s+e)/2;
return query(s, mid, node*2, l, r) + query(mid+1, e, node*2+1, l, r);
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 8983번 사냥꾼 (Java) (0) | 2022.02.04 |
|---|---|
| [BOJ] 백준 1561번 놀이 공원 (Java) (0) | 2022.02.03 |
| [BOJ] 백준 12846번 무서운 아르바이트 (Java) (0) | 2022.02.01 |
| [BOJ] 백준 1615번 교차개수세기 (Java) (0) | 2022.01.31 |
| [BOJ] 백준 5419번 북서풍 (Java) (0) | 2022.01.30 |




