#1788 피보나치 수의 확장
난이도 : 실버 2
유형 : DP
1788번: 피보나치 수의 확장
첫째 줄에 F(n)이 양수이면 1, 0이면 0, 음수이면 -1을 출력한다. 둘째 줄에는 F(n)의 절댓값을 출력한다. 이 수가 충분히 커질 수 있으므로, 절댓값을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
▸ 문제
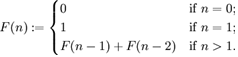
수학에서, 피보나치 수는 위의 점화식과 같이 귀납적으로 정의되는 수열이다. 위의 식에서도 알 수 있듯이, 피보나치 수 F(n)은 0 이상의 n에 대해서만 정의된다.
하지만 피보나치 수 F(n)을 n이 음수인 경우로도 확장시킬 수 있다. 위의 식에서 n>1인 경우에만 성립하는 F(n)=F(n-1)+F(n-2)를 n<=1일 때도 성립되도록 정의하는 것이다. 예를 들어 n=1일 때 F(1)=F(0)+F(-1)이 성립되어야 하므로, F(-1)은 1이 되어야 한다.
n이 주어졌을 때, 피보나치 수 F(n)을 구하는 프로그램을 작성하시오. n은 음수로 주어질 수도 있다.
▸ 입력
첫째 줄에 n이 주어진다. n은 절댓값이 1,000,000을 넘지 않는 정수이다.
▸ 출력
첫째 줄에 F(n)이 양수이면 1, 0이면 0, 음수이면 -1을 출력한다. 둘째 줄에는 F(n)의 절댓값을 출력한다. 이 수가 충분히 커질 수 있으므로, 절댓값을 1,000,000,000으로 나눈 나머지를 출력한다.
문제 풀이 🖋
간단한 피보나치 문제에서 약간 응용되어 나온 문제이다. 피보나치의 값이 음수,양수에 대한 정보를 출력하고 그에 대한 피보나치의 수를 출력해주면 된다.
📚 조건
∙ |n| < 1,000,000
피보나치가 음수인 경우는 0보다 작고 2로 나누어질 때이다.
F(1) = F(0) + F(-1) = 0 + 1 > F(-1) = 1
F(0) = F(-1) + F(-2) = 1 + (-2) > F(-2) = -2
F(-1) = F(-2) + F(-3) = (-2) + 3 > F(-3) = 3
F(-2) = F(-3) + F(-4) = 3 + (-5) > F(-4) = -5
...
위와 같이 보면 자연스럽게 n이 음수일 때, 피보나치의 수는 양수 피보나치의 수와 일치하는데, 2의 배수인 경우에만 음수가 되는 규칙을 찾을 수 있다.
그래서 음수 피보나치 수를 구할 때는 그냥 평소대로 양수 피보나치의 수를 구해준 다음 2의 배수인 경우 그에 대한 음수 값을 출력해주면 된다.
풀이 코드 ✔︎
1. Top-down
import java.io.*;
import java.util.Arrays;
public class Main {
static int[] dp;
static final int mod = 1_000_000_000;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
if(n>0) {
System.out.println(1);
}else if (n<0) {
n = -n;
if(n%2 ==0) {
System.out.println(-1);
}else {
System.out.println(1);
}
}else {
System.out.println(0);
}
dp = new int[n+1];
Arrays.fill(dp, -1);
System.out.println(fibo(n));
}
static int fibo(int x) {
if( x==0) return 0;
if(x ==1 || x==2) return 1;
if(dp[x] != -1) return dp[x];
return dp[x] = (fibo(x-1)%mod + fibo(x-2)%mod)%mod;
}
}
2. Bottom-up
import java.io.*;
public class Main {
static int[] dp;
static final int mod = 1_000_000_000;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
if(n>0) {
System.out.println(1);
}else if (n<0) {
n = -n;
if(n%2 ==0) {
System.out.println(-1);
}else {
System.out.println(1);
}
}else {
System.out.println(0);
}
dp = new int[1_000_001];
dp[1] = 1;
dp[2] = 1;
for(int i=3; i<n+1; i++) {
dp[i] = (dp[i-1] + dp[i-2])%mod;
}
System.out.println(dp[n]);
}
}
이 문제는 재귀호출을 사용한 탑다운과 포문 n번을 돌리는 바텀업과의 시간차이가 꽤 발생했다. 확실히 재귀호출을 하지 않으니 메모리 사용량과 시간을 줄일 수 있다
그래도 이해하기 쉬운 것은 탑다운이 좀 더 직관적으로 다가온다.


+탑다운과 바텀업에 대한 재밌는 글이 있어서 공유한다.
Top Down vs Bottom Up
본 포스팅은 Code Complete 책이 지닌 정보를 재가공하여 올림을 알립니다. 안녕하세요 ! 오늘은 Top Down vs Bottom Up을 주제로 들고 왔습니다. Top Down, Bottom Up 개념의 경우 알고리즘 문제를 풀 때 많이
ggodong.tistory.com
너무나 추상적인 탑다운? 조밀조밀 설계의 왕 바텀업?
설계는 탑다운이 쉽지만 효율은 바텀업이 더 좋다. 아무래도 재귀함수 퍼포먼스가 좋은 편은 아니고 함수 하나하나의 요소가 중요하다
그렇다고 바텀업의 단점은 이 접근 방법만 사용해서 개발하기 힘들다. 완벽한 설계를 할 수 있다는 보장은 어디에도 없다. 레고를 조립할 때 보면 꼭 부품이 하나씩 남는 것 처럼 말이다.
둘은 배타적인 개념이 아니라 상호 보완적인 개념이라는 것에 동의한다.

'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 9658번 돌 게임4 (Java) (0) | 2021.06.04 |
|---|---|
| [BOJ] 백준 1766번 문제집 (Java) (0) | 2021.06.03 |
| [BOJ] 백준 1793번 타일링 (Java) (0) | 2021.06.02 |
| [BOJ] 백준 1068번 트리 (Java) (0) | 2021.06.02 |
| [BOJ] 백준 13549번 숨바꼭질3 (Java) (0) | 2021.06.01 |




