세그먼트 트리
세그먼트(Segment)는 영어 뜻 자체로는 분할, 단편, 구분 등의 의미를 가진다. 자료구조에서 세그먼트 트리는 트리 영역에서 중요한 개념으로 연속된 구간의 데이터의 합을 가장 빠르고 간단하게 구할 수 있는 트리이다.
선형 탐색을 이용한 구간 합
보자마자 가장 기본적으로 생각나는 방법은 선형탐색을 하여 값을 더해주는 것이다.
배열 [ 1 2 3 4 5 ]에서 특정 구간의 합을 그냥 생각나는대로 구해보자. 2번부터 5번의 구간 합을 구하려면 말 그대로 2번 부터 5번의 합을 모조리 더해주면 된다.
| idx | 2 | 3 | 4 | 5 |
| sum | 2 | 5 | 9 | 14 |
그런데 이러한 방식은 시간복잡도 O(n)으로 간단하지만 속도가 느리다는 단점을 가지고 있다. 만약 10만개의 데이터에서 1만개의 구간 합을 구하려면 10억번의 연산을 해야한다.
트리 구조를 이용한 구간 합
더 빠르게 값을 구할 수 있는 알고리즘이 바로 세그먼트 트리라는 자료구조이다. 트리의 특성상 합을 구할 때 시간 복잡도는 O(logN)을 가진다.
구간 합 트리 생성
기존의 배열을 [ 1 2 3 4 5 ]을 트리 구조를 이용해서 구간 합 트리를 생성해보자.

루트 노드에는 모든 원소를 더한 값이 들어간다. 2번째 노드에는 1~3번 원소의 합을, 3번째 노드에는 4~5번 원소의 합을 구해준다. 이러한 방식으로 각각 반으로 세그먼트를 시작하여 리프노드가 나올 때 까지 구간 합들을 저장해주면 된다.
위의 코드는 재귀적으로 탐색하여 stack방식을 이용하는 것이 편하다.
static long pSum(int start, int end, int node, int l, int r) {
if(r < start || l> end ) return 0;
if(l <= start && end <= r )return tree[node];
int mid = (start+end)/2;
return pSum(start, mid, node*2, l, r) + pSum(mid+1, end, node*2+1, l, r);
}
→ 주의할 점은 구간 합 트리는 항상 구간의 합을 가지고 있는 형태이므로 노드의 인덱스 값과 헷갈리면 안된다.
배열 크기의 최댓값
구간 합 트리를 보면 이진 트리임을 알 수 있다. 이진 트리 중 모든 노드가 꽉차있는 완전 이진트리일 경우 가장 많은 데이터를 가진다. 그래서 배열의 크기 N이 주어졌을 때 완전 이진 트리의 크기를 구해주면 된다.
완전 이진트리 특성 상 h>=1, 2^(h-1) < N <= 2^h가 성립하므로 각 항에 log2를 넣어주면 높이 h-1 < log2(N) <=h 임을 알 수 있다.
// log2(N)
int h = (int) Math.ceil(Math.log(N) / Math.log(2));
트리의 노드 갯수는 첫째 항은 루트 노드로 1, 공비가 r =2이고 n은 높이(h)를 나타내는 등비수열이다.

공식에 따라 구하면 1+2+4+...+2^(h) = 2^(h+1)-1이다.
int treeSize = (int) Math.pow(2, h + 1) - 1;ex) 배열의 크기가 5인 트리의 최대 크기를 구해보자.
N=5이므로 트리의 높이 h = 3이다.
따라서, 트리의 사이즈는 2^4-1 = 15이다.
→ 2^0 + 2^1 + 2^2 + 2^3 = 15
그런데 세그먼트 트리를 사용할 때에는 루트노드 index를 1로 저장해줄 것이기 때문에 +1을 사용하여 배열 크기를 생성해주면 된다.
// 루트 노드 index 1로 시작 할 경우 size+1
int treeSize = (int)Math.pow(2, h + 1);
특정 원소의 값을 수정하는 함수 만들기 (구간 합 update)
배열에 있는 특정 원소의 값을 수정할 때는 해당 원소를 포함하고 있는 모든 구간의 합 노드들을 갱신해줘야 한다.
예를 들어 [ 1 2 3 4 5 ]을 [ 1 2 6 4 5 ]로 바꾸면 구간 합 트리는 다음과 같이 update되어야 한다.
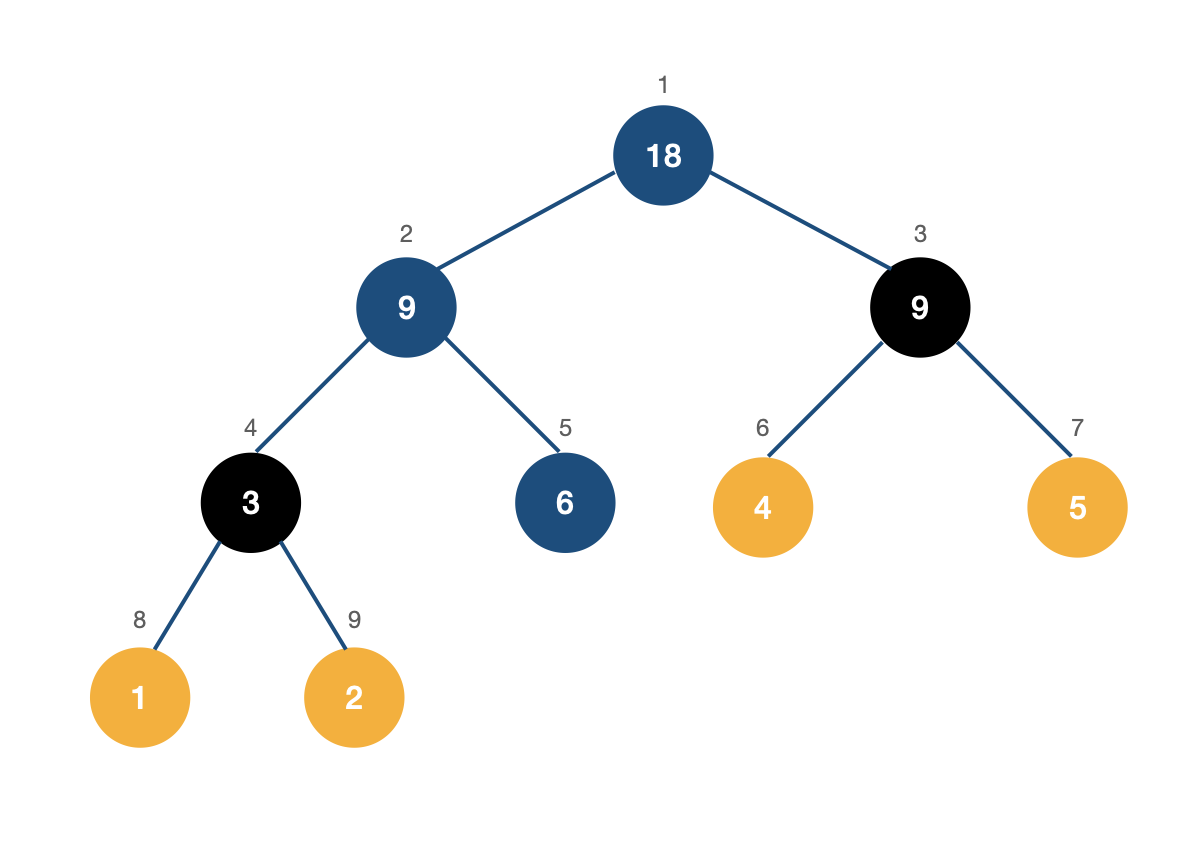
이 함수 또한 재귀적으로 탐색하여 쉽게 변경할 수 있다. 트리를 탐색하면서 idx를 포함하고 있는 곳들을 찾아 갱신해주면 된다. if(start <= idx && idx <= end)
ex) s~e : tree[node] += dif;
0~4 : 15 > 18
0~2 : 6 > 9
2~2 : 3 > 6
// 배열 idx =2
// 변경값 dif = (새로운 값 - 원래 값) = 6 - 3 = 3
static void update(int start, int end, int node, int idx, long dif) {
if(start <= idx && idx <= end) {
tree[node] += dif;
}else return;
if(start == end) return;
int mid = (start+end)/2;
update(start, mid, node*2, idx, dif);
update(mid+1, end, node*2+1, idx, dif);
}
선형 탐색 vs 세그먼트 트리 성능 비교
백준 2042번 구간합 구하기 문제를 풀면서 두 가지 방법의 성능을 비교해보았다.
선형 탐색은 값을 바꾸는데 O(1), 값을 더하는데 O(N)이니 M번 수행한다 하면 O(NM)의 시간이 걸린다.
세그먼트 트리로 하면은 값을 바꾸는데 O(logN), 값을 더하는데 O(logN)으로 M번 수행하면 O(MlogN)이 걸린다.


위의 결과를 보면 시간이 거의 9~10배 정도 차이가 나는 것을 볼 수 있다. 데이터가 많아지면 많아질수록 엄청난 성능 차이를 보일 것이다. 이렇게 세그먼트 트리로 구간 합을 구하면 기존 선형탐색 방법보다 효율을 엄청나게 높이며 코딩을 할 수 있다. O(MlogN)
세그먼트 트리를 사용한 구간 합 전체 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int n;
static long[] tree,arr;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
arr = new long[n];
tree = new long[getTreeSize()];
for(int i=0; i<n; i++) {
arr[i] = Long.parseLong(br.readLine());
}
init(0, n-1, 1);
while(true) {
if(m==0 && k==0) break;
st = new StringTokenizer(br.readLine());
int op = Integer.parseInt(st.nextToken());
if(op ==1) {
int idx = Integer.parseInt(st.nextToken())-1;
long num = Long.parseLong(st.nextToken());
long dif = num - arr[idx];
update(0, n-1, 1, idx, dif);
arr[idx] = num;
m--;
}else {
int left = Integer.parseInt(st.nextToken())-1;
int right = Integer.parseInt(st.nextToken())-1;
long sum =pSum(0, n-1, 1, left, right);
sb.append(sum+"\n");
k--;
}
}
System.out.println(sb.toString());
}
// 구간 합 트리 사이즈 구하기
static int getTreeSize() {
int h = (int)Math.ceil(Math.log(n)/Math.log(2)) +1;
return (int)Math.pow(2, h)-1;
}
// 구간 합 트리 초기값 설정하기
static long init(int start, int end, int node) {
if(start == end) return tree[node] = arr[start];
int mid = (start+end)/2;
return tree[node] = init(start, mid, node*2) + init(mid+1, end, node*2+1);
}
// 구간 합 트리 값 수정하기
static void update(int start, int end, int node, int idx, long dif) {
if(start <= idx && idx <= end) {
tree[node] += dif;
}else return;
if(start == end) return;
int mid = (start+end)/2;
update(start, mid, node*2, idx, dif);
update(mid+1, end, node*2+1, idx, dif);
}
// [ l ~ r ] 구간 합 구하기
static long pSum(int start, int end, int node, int l, int r) {
if(r < start || l> end ) return 0;
if(l <= start && end <= r )return tree[node];
int mid = (start+end)/2;
return pSum(start, mid, node*2, l, r) + pSum(mid+1, end, node*2+1, l, r);
}
}
'Dot Algo∙ DS > 자료구조' 카테고리의 다른 글
| [자료구조] 힙(Heap) 구현하기 - 우선순위 큐 (Java) (0) | 2022.01.05 |
|---|---|
| 트라이(Trie) 문자열 탐색 트리 개념 정리 (Java) (0) | 2021.09.08 |
| [자료구조] BinaryTree 정리 (Java) (0) | 2021.04.09 |
| [자료구조] Stack와 Queue 정리 (Java) (0) | 2021.04.06 |
| [자료구조] ArrayList와 LinkedList정리 (Java) (0) | 2021.04.04 |




