#10868 최솟값
난이도 : 골드 1
유형 : 자료 구조 / 세그먼트 트리
10868번: 최솟값
N(1 ≤ N ≤ 100,000)개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지 중에서 제일 작은 정수를 찾는 것은 어려운 일이 아니다. 하지만 이와 같은 a, b의 쌍이 M(1 ≤ M ≤ 100,000)개 주어졌을 때는
www.acmicpc.net
▸ 문제
N(1 ≤ N ≤ 100,000)개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지 중에서 제일 작은 정수를 찾는 것은 어려운 일이 아니다. 하지만 이와 같은 a, b의 쌍이 M(1 ≤ M ≤ 100,000)개 주어졌을 때는 어려운 문제가 된다. 이 문제를 해결해 보자.
여기서 a번째라는 것은 입력되는 순서로 a번째라는 이야기이다. 예를 들어 a=1, b=3이라면 입력된 순서대로 1번, 2번, 3번 정수 중에서 최솟값을 찾아야 한다. 각각의 정수들은 1이상 1,000,000,000이하의 값을 갖는다.
▸ 입력
첫째 줄에 N, M이 주어진다. 다음 N개의 줄에는 N개의 정수가 주어진다. 다음 M개의 줄에는 a, b의 쌍이 주어진다.
▸ 출력
M개의 줄에 입력받은 순서대로 각 a, b에 대한 답을 출력한다.
문제 풀이
세그먼트 트리에 대한 개념이 있어야 풀 수 있는 문제이다. 각 배열의 구간에 따른 원소의 최솟값을 트리에 저장한 다음 해당 구간을 조회하면서 최솟값을 구해야 한다.
📚 조건
- N개의 정수 ( 1 <= N <= 100,000 )
- 구간(a,b)의 쌍 M개 (1 <= M <= 100,000)
N개의 원소가 들어있는 데이터를 (a~b)구간을 M번 선형 탐색 O(NM)의 시간이 걸린다.
→ 세그먼트 트리로 하면은 값을 바꾸는데 O(logN), 탐색하는데 O(logN)으로 M번 수행하면 O(MlogN)으로 줄일 수 있다.
구상
- 주어진 N개의 정수로 최소 세그먼트 트리를 생성한다.
- 주어진 구간 (a,b)로 최소 트리를 탐색하면서 구간 내의 최솟을 출력한다.
스케치
∙ 1번 로직
해당 배열로 최소 세그먼트 트리를 만들어보자.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 75 | 30 | 100 | 38 | 50 | 51 | 52 | 20 | 81 | 5 |
1-1) 세그먼트 트리 크기 구하기
세그먼트 트리는 이진 트리이다. 이진 트리 중 모든 노드가 꽉차있는 완전 이진트리일 경우 가장 많은 데이터를 가진다. 그래서 배열의 크기 N이 주어졌을 때 완전 이진 트리의 크기를 구해주면 된다.
트리의 노드 갯수는 첫째 항은 루트 노드로 1, 공비가 r =2이고 n은 높이(h)를 나타내는 등비수열이다.
등비수열 합 공식에 따라 구하면 1+2+4+...+2^(h) = 2^(h+1)-1이다. 그런데 나는 세그먼트 트리를 사용할 때에는 루트노드 index를 1로 저장해줄 것이기 때문에 +1을 사용하여 배열 크기를 생성해주면 된다.
int h = (int) Math.ceil(Math.log(N) / Math.log(2));
int treeSize = (int)Math.pow(2, h + 1);
1-2) 세그먼트 트리 생성
그림과 같이 구간 내에서 최솟값을 가지는 원소를 트리에 넣어줌으로써 최소트리를 만들어 주면 된다.

∙ 2번 로직
구간 6~9에서의 최솟값을 구하라고 한다면 아래에 빨간 동그라미를 친 부분과 같이 6번 노드(6~8)와 14번 노드(9~9)의 값을 비교해서 구해주면 된다.
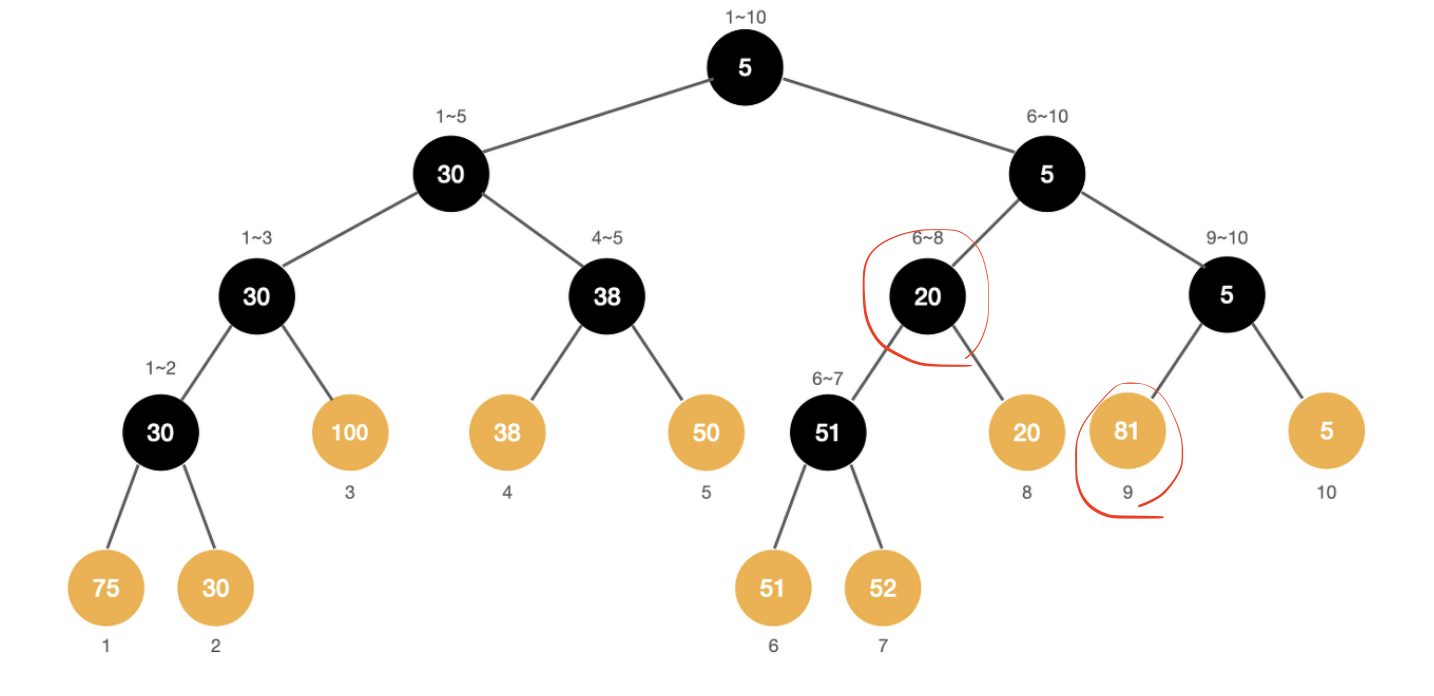
색칠
∙ 1번 로직 코드
루트 노드를 1번으로 하는 이유는 왼쪽 자식 노드와 오른쪽 자식 노드의 인덱스를 매기기 편하기 때문이다.
왼쪽 자식 노드 : node*2, 오른쪽 자식 노드 : node*2+1
// 1-1. 세그먼트 트리 사이즈 구하기
static int getTreeSize() {
int h = (int)Math.ceil(Math.log(n)/Math.log(2)) +1;
return (int)Math.pow(2,h);
}
// 1-2. 세그먼트 트리 생성
static void init(int start, int end, int node) {
if(start == end) {
tree[node] = elements[start];
}else{
int mid = (start+end)/2;
init(start, mid, node*2);
init(mid+1, end, node*2+1);
if(tree[node*2] < tree[node*2+1]) {
tree[node] = tree[node*2];
}else {
tree[node] = tree[node*2+1];
}
}
}
∙ 2번 로직 코드
// 2. 구간 [l,r] 최소 구하기
static void getMin(int start, int end, int node, int l, int r) {
if(end < l || r < start) return;
if(l<= start && end <= r) {
result = Math.min(result, tree[node]);
return;
}
int mid = (start+end)/2;
getMin(start, mid, node*2, l,r);
getMin(mid+1, end, node*2+1, l, r);
}
}
풀이 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main{
static int n, result, Init = Integer.MAX_VALUE;
static int[] elements, tree;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
elements = new int[n+1];
for(int i=1; i<n+1; i++) {
elements[i] = Integer.parseInt(br.readLine());
}
int treeSize = getTreeSize();
tree = new int[treeSize];
init(1,n,1);
for(int i=0; i<m; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
result = Init;
getMin(1, n, 1, a, b);
sb.append(result+"\n");
}
System.out.println(sb.toString());
}
static int getTreeSize() {
int h = (int)Math.ceil(Math.log(n)/Math.log(2)) +1;
return (int)Math.pow(2,h);
}
static void init(int start, int end, int node) {
if(start == end) {
tree[node] = elements[start];
}else{
int mid = (start+end)/2;
init(start, mid, node*2);
init(mid+1, end, node*2+1);
if(tree[node*2] < tree[node*2+1]) {
tree[node] = tree[node*2];
}else {
tree[node] = tree[node*2+1];
}
}
}
static void getMin(int start, int end, int node, int l, int r) {
if(end < l || r < start) return;
if(l<= start && end <= r) {
result = Math.min(result, tree[node]);
return;
}
int mid = (start+end)/2;
getMin(start, mid, node*2, l,r);
getMin(mid+1, end, node*2+1, l, r);
}
}

'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 1202번 보석 도둑 (Java) (0) | 2021.06.24 |
|---|---|
| [BOJ] 백준 2468번 안전 영역 (Java) (0) | 2021.06.24 |
| [BOJ] 백준 11403번 경로 찾기 (Java) (0) | 2021.06.23 |
| [BOJ] 백준 2357번 최솟값과 최댓값 (Java) (0) | 2021.06.22 |
| [BOJ] 백준 1935번 후위 표기식2 (Java) (0) | 2021.06.21 |




