#4883 삼각 그래프
난이도 : 실버 1
유형 : DP
4883번: 삼각 그래프
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 그래프의 행의 개수 N이 주어진다. (2 ≤ N ≤ 100,000) 다음 N개 줄에는 그래프의 i번째 행에 있는 정점의 비용이
www.acmicpc.net
▸ 문제
이 문제는 삼각 그래프의 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 가는 최단 경로를 찾는 문제이다.
삼각 그래프는 사이클이 없는 그래프로 N ≥ 2 개의 행과 3열로 이루어져 있다. 삼각 그래프는 보통 그래프와 다르게 간선이 아닌 정점에 비용이 있다. 어떤 경로의 비용은 그 경로에서 지나간 정점의 비용의 합이다.
오른쪽 그림은 N = 4인 삼각 그래프이고, 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 경로 중 아래로만 가는 경로의 비용은 7+13+3+6 = 29가 된다. 삼각 그래프의 간선은 항상 오른쪽 그림과 같은 형태로 연결되어 있다.
▸ 입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 그래프의 행의 개수 N이 주어진다. (2 ≤ N ≤ 100,000) 다음 N개 줄에는 그래프의 i번째 행에 있는 정점의 비용이 순서대로 주어진다. 비용은 정수이며, 비용의 제곱은 1,000,000보다 작다.
입력의 마지막 줄에는 0이 하나 주어진다.
▸ 출력
각 테스트 케이스에 대해서, 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 가는 최소 비용을 테스트 케이스 번호와 아래와 같은 형식으로 출력한다.
k. n
k는 테스트 케이스 번호, n은 최소 비용이다.
📚 조건
- 행의 개수 N (2 ≤ N ≤ 100,000)
- 비용 제곱 dp[i] ( dp[i]^2 < 1,000,000, 음수 가능)
문제 풀이
가장 위쪽 가운데 (0,1)에서 가장 아래쪽 가운데 (n-1, 1)로 가는 최단 경로를 구하면 된다. 각 노드의 비용은 음수도 가능하므로 최단경로를 구한다고 되는 것이 아니라 모든 경로를 조사해줘야 한다.
특이사항은 각 열마다 움직일 수 있는 경로가 다르다는 것이다. 시작점이 있는 0번째 행과 바로 그 아래에 있는 1번째 행에서는 (0,1)에서 무조건 시작해야하므로 따로 값을 입력해줘야하고 나머지는 규칙을 찾아 설계해주면 된다.
0 → 1번째 행 정점 이동경로
(1,0)은 (0,1)에서 이동한 경우만 가능하다.
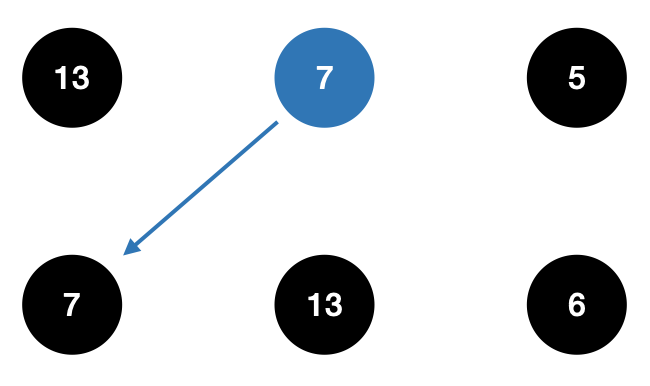
(1,1), (1,2)는 각 3가지의 경우가 존재한다. 가장 작은 비용이 드는 경로로 이동해주면 된다.


그 외 나머지 행 정점 이동경로

점화식으로 나타내면 다음과 같다.
dp[i][0] += Math.min(dp[i-1][0], dp[i-1][1]);
dp[i][1] += Math.min(Math.min(dp[i][0], dp[i-1][0]), Math.min(dp[i-1][1], dp[i-1][2]));
dp[i][2] += Math.min(dp[i][1],Math.min(dp[i-1][1], dp[i-1][2]));
풀이 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
String line;
int tc=0;
while(Integer.parseInt((line=br.readLine()))!= 0) {
tc++;
int n = Integer.parseInt(line);
int[][] dp = new int[n][3];
for(int i=0; i<n; i++) {
st = new StringTokenizer(br.readLine());
dp[i][0] = Integer.parseInt(st.nextToken());
dp[i][1] = Integer.parseInt(st.nextToken());
dp[i][2] = Integer.parseInt(st.nextToken());
}
for(int i=1; i<n; i++) {
if(i==1) {
for(int j=0; j<3; j++) {
if(j==0) dp[i][0] += dp[i-1][1];
else {
dp[i][j] += Math.min(dp[i][j-1],
Math.min(dp[i-1][1], dp[i-1][1]+dp[i-1][2]));
}
}
}else {
dp[i][0] += Math.min(dp[i-1][0], dp[i-1][1]);
dp[i][1] += Math.min(Math.min(dp[i][0], dp[i-1][0]),
Math.min(dp[i-1][1], dp[i-1][2]));
dp[i][2] += Math.min(dp[i][1],Math.min(dp[i-1][1], dp[i-1][2]));
}
}
System.out.println(tc+". "+dp[n-1][1]);
}
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 1854번 K번째 최단경로 찾기 (Java) (0) | 2021.07.16 |
|---|---|
| [BOJ] 백준 9205번 맥주 마시면서 걸어가기 (Java) (2) | 2021.07.15 |
| [BOJ] 백준 1325번 효율적인 해킹 (Java) (0) | 2021.07.13 |
| [BOJ] 백준 1197번 최소 스패닝 트리 (Java) (0) | 2021.07.12 |
| [BOJ] 백준 10422번 괄호 (Java) (1) | 2021.07.11 |




