[프로그래머스] 2021 카카오 인턴 #3 표 편집 (Java)

#3 표 편집

난이도 : LEVEL 3

유형 : Stack || 양방향 연결리스트

코딩테스트 연습 - 표 편집

8 2 ["D 2","C","U 3","C","D 4","C","U 2","Z","Z"] "OOOOXOOO" 8 2 ["D 2","C","U 3","C","D 4","C","U 2","Z","Z","U 1","C"] "OOXOXOOO"

programmers.co.kr

문제

[본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]

업무용 소프트웨어를 개발하는 니니즈웍스의 인턴인 앙몬드는 명령어 기반으로 표의 행을 선택, 삭제, 복구하는 프로그램을 작성하는 과제를 맡았습니다. 세부 요구 사항은 다음과 같습니다

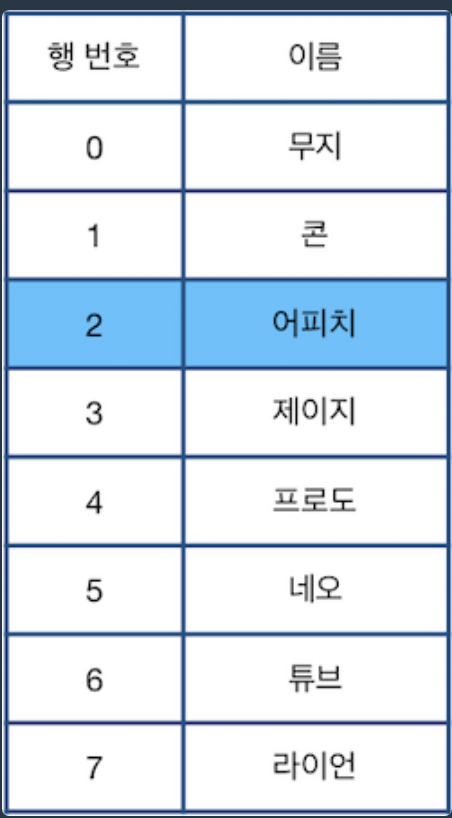
위 그림에서 파란색으로 칠해진 칸은 현재 선택된 행을 나타냅니다. 단, 한 번에 한 행만 선택할 수 있으며, 표의 범위(0행 ~ 마지막 행)를 벗어날 수 없습니다. 이때, 다음과 같은 명령어를 이용하여 표를 편집합니다.

"U X": 현재 선택된 행에서 X칸 위에 있는 행을 선택합니다.
"D X": 현재 선택된 행에서 X칸 아래에 있는 행을 선택합니다.
"C" : 현재 선택된 행을 삭제한 후, 바로 아래 행을 선택합니다. 단, 삭제된 행이 가장 마지막 행인 경우 바로 윗 행을 선택합니다.
"Z" : 가장 최근에 삭제된 행을 원래대로 복구합니다. 단, 현재 선택된 행은 바뀌지 않습니다.

예를 들어 위 표에서 "D 2"를 수행할 경우 아래 그림의 왼쪽처럼 4행이 선택되며, "C"를 수행하면 선택된 행을 삭제하고, 바로 아래 행이었던 "네오"가 적힌 행을 선택합니다(4행이 삭제되면서 아래 있던 행들이 하나씩 밀려 올라오고, 수정된 표에서 다시 4행을 선택하는 것과 동일합니다).

제한사항

5 ≤ n ≤ 1,000,000
0 ≤ k < n
1 ≤ cmd의 원소 개수 ≤ 200,000
- cmd의 각 원소는 "U X", "D X", "C", "Z" 중 하나입니다.
- X는 1 이상 300,000 이하인 자연수이며 0으로 시작하지 않습니다.
- X가 나타내는 자연수에 ',' 는 주어지지 않습니다. 예를 들어 123,456의 경우 123456으로 주어집니다.
- cmd에 등장하는 모든 X들의 값을 합친 결과가 1,000,000 이하인 경우만 입력으로 주어집니다.
- 표의 모든 행을 제거하여, 행이 하나도 남지 않는 경우는 입력으로 주어지지 않습니다.
- 본문에서 각 행이 제거되고 복구되는 과정을 보다 자연스럽게 보이기 위해 "이름" 열을 사용하였으나, "이름"열의 내용이 실제 문제를 푸는 과정에 필요하지는 않습니다. "이름"열에는 서로 다른 이름들이 중복없이 채워져 있다고 가정하고 문제를 해결해 주세요.
표의 범위를 벗어나는 이동은 입력으로 주어지지 않습니다.
원래대로 복구할 행이 없을 때(즉, 삭제된 행이 없을 때) "Z"가 명령어로 주어지는 경우는 없습니다.
정답은 표의 0행부터 n - 1행까지에 해당되는 O, X를 순서대로 이어붙인 문자열 형태로 return 해주세요.

정확성 테스트 케이스 제한 사항

5 ≤ n ≤ 1,000
1 ≤ cmd의 원소 개수 ≤ 1,000

효율성 테스트 케이스 제한 사항

주어진 조건 외 추가 제한사항 없습니다.

문제 풀이

이러한 유형은 뭔가 애매해서 어렵다. 직접 ListNode를 설계해서 풀면 풀이도 오래걸리면서 어렵게 접근하는 것 같고 또 가볍게 접근하자하니 효율성에서 막힐것 같아 스타트에서 많이 머뭇거렸다. 실전에서 이런 문제가 나오면 가장 마지막에 풀이를 해야겠다.

일단 제한사항을 확인해보자.

5 ≤ n ≤ 1,000,000

n의 최댓값은 100만이다. 이를 String 데이터("OOOXOXOX...")로 출력해야하는데 해당 데이터를 배열로 공간할당하고 명령 최대 20만개를 연산한다고 하기만해도 벌써부터 효율성 최악임이 느껴진다.

그래서 주먹구구식으로 boolean[] status = new boolean[100만]으로 상태를 체크해주는 풀이는 무리라고 생각했다. 행의 위치를 나타내는 cursor를 단순 상태값으로 나타낸 다음 제외된 표들의 정보를 받아올 수 있는 방향으로 설계를 잡았다. 100만개의 상태 관리를 어떻게 해야할지 감이 안잡혔다. 이때 양방향 연결리스트를 생각했는데 일단 뒤로 미뤄놓고 좀 더 쉬운 방법이 없나 고민을 해보았다.

이 조건들을 보면 최대한 예외가 발생하지 않도록 데이터를 친절하게 제공해줬다고 느꼈다. 예외처리에서 크게 신경쓸 부분이 없을 것 같다.

표의 범위를 벗어나는 이동은 입력으로 주어지지 않습니다.
원래대로 복구할 행이 없을 때(즉, 삭제된 행이 없을 때) "Z"가 명령어로 주어지는 경우는 없습니다.
표의 모든 행을 제거하여, 행이 하나도 남지 않는 경우는 입력으로 주어지지 않습니다.
cmd에 등장하는 모든 X들의 값을 합친 결과가 1,000,000 이하인 경우만 입력으로 주어집니다.

결국 쉬운 방법이 생각안나서 양방향 연결리스트로 풀이를 하였다.

구현

U,D,C,Z 이 4가지의 연산을 구현해주면 되는데 연산 자체는 간단하다.

U와 D는 단순 커서를 이동해주면 된다.
C는 행 삭제, 커서의 위치는 그대로 냅둔다.
- 예외는 마지막 행인 경우 바로 윗 행 선택한다.
Z는 가장 최근에 삭제된 행 복구를 해준다
- 행 복구는 선입선출 구조로 Stack을 사용해서 삭제된 데이터를 저장해주면 된다.
- 복구된 행이 현재 커서 위치보다 작거나 같으면 커서 위치를 한 칸 내려준다.

StringBuffer나 StringBuilder에 setCharAt(int idx, char c)이라는 메소드가 있다. 이는 시간복잡도 O(1)로 문자열 idx의 값을 c로 변경해주는 함수로 제외된 행의 번호 데이터만 있으면 쉽게 답을 출력할 수 있다.

양방향 ListNode 풀이 코드

쉬운 풀이가 생각이 안나 양방향 ListNode를 구현해서 풀이를 해보았다. java로 ListNode구현하기 참고

커서가 주어졌기 때문에 무작위적으로 삽입,삭제가 이루어지지 않아서 구현은 까다롭지않았다.

Node init(size) : 한 번에 사이즈가 n인 인접리스트를 만들어준다.

C,Z 연산 : remove를 하면 해당 노드는 사라지지 않고 연결만 끊어줬다가 restore를 하게되면 다시 연결시켜준다.

import java.util.Stack;

class Solution {
	static Stack<Node> dStack;
	// 양방향 연결리스트 
	static class Node{
		int data;
		Node prev, next;
		
		public Node() {
			/* no-op */
		}
		
		public Node(int data) {
			this.data = data;
			this.prev = null;
			this.next = null;
		}
		
		public Node remove() {
			prev.next = next;
			next.prev = prev;
			if(this.next.data == -1) {
				return this.prev;
			}else {
				 return this.next;
			}
		}
		public void restore() {
			prev.next = this;
			next.prev = this;
		}
	}
    
	// 노드 초기화
	public static Node init(int size) {
		Node initNode = new Node(-1);
		Node prevNode = initNode;
		Node curNode = null;
		
		for(int i=0; i<size; i++) {
			curNode = new Node(i);
			prevNode.next = curNode;
			curNode.prev = prevNode;
			
			prevNode = curNode;
		}
		
		// endNode (idx =size인 노드) 
		Node endNode = new Node(-1);
		curNode.next = endNode; 
		return initNode.next; // 초기값 0번노드 
	}
    
	public String solution(int n, int k, String[] cmd) {
		Node cursor = init(n);
		dStack = new Stack<>();
		for(int i=0; i<k; i++) {
			cursor = cursor.next;
		}
		
		for(int i=0; i<cmd.length; i++) {
			String[] command_line = cmd[i].split(" ");
			char op = command_line[0].charAt(0);
			if(op=='D') {
				int opNum = Integer.parseInt(command_line[1]);
				cursor = down(cursor, opNum);
			}else if(op=='U') {
				int opNum = Integer.parseInt(command_line[1]);
				cursor = up(cursor, opNum);
			}else if(op=='C') {
				cursor = delete(cursor);
			}else {
				restore();
			}
		}
		
		StringBuilder answer = new StringBuilder();
		for(int i=0; i<n; i++) {
			answer.append("O");
		}
		
		while(!dStack.isEmpty()) {
			answer.setCharAt(dStack.pop().data, 'X');
		}
		return answer.toString();
	}
    
	static Node down(Node cur, int num) {
		for(int i=0; i<num; i++) {
			cur = cur.next;
		}
		return cur;
	}
	static Node up(Node cur, int num) {
		for(int i=0; i<num; i++) {
			cur = cur.prev;
		}
		return cur;
	}
	static Node delete(Node cur) {
		dStack.push(cur);
		cur = cur.remove();
		return cur;
	}
	static void restore() {
		Node bNode = dStack.pop();
		bNode.restore();
	}

}

단순 풀이 코드

이 풀이는 구글링을 통해 참고하였다. U, D, C, Z연산의 동작방식은 위와 똑같다. 표와 커서를 있는 그대로 표현해주었다. 이게 바로 내가 고민하다 실패한 쉽게 접근하는 방법인 것 같다.

예제에서 보이는 것처럼 그대로 1번 커서에서 'C'연산이 작동하 chart_size는 7에서 6으로 줄어들고 커서는 1 그대로 냅둔다.

이렇게 삭제된 행은 stack에 쌓아둔다. 해당 풀이는 절대적 위치가 아닌 상대적 위치를 저장해줬기 때문에 결과값은 chart_size로 현재 남아있는 행을 받아온 다음 StringBuilder에서 제공하는 insert(int idx, 'X')로 삭제된 행 인덱스에 'X'를 넣어줌으로써 나타냈다.

import java.util.Arrays;
import java.util.Stack;

class Solution {
    static int cursor,chart_size;
    static Stack<Integer> dStack;
    public String solution(int n, int k, String[] cmd) {
        chart_size = n; cursor = k;
        dStack = new Stack<>();

        for(int i=0; i<cmd.length; i++) {
            String[] command_line = cmd[i].split(" ");
            char op = command_line[0].charAt(0);

            if(op=='D') {
                int opNum = Integer.parseInt(command_line[1]);
                down(opNum);
            }else if(op=='U') {
                int opNum = Integer.parseInt(command_line[1]);
                up(opNum);
            }else if(op=='C') {
                chart_size--;
                delete();
            }else {
                chart_size++;
                restore();
            }
        }

        StringBuilder sb = new StringBuilder();
        for(int i = 0; i <chart_size ; i++) {
            sb.append('O');
        }
        while(!dStack.isEmpty()) {
            sb.insert(dStack.pop().intValue(), 'X');
        }
        return sb.toString();
    }

	static void down(int num) {
		cursor += num;
	}
	static void up(int num) {
		cursor -= num;
	}
	static void delete() {
		dStack.push(cursor);
		if(cursor== chart_size) cursor--;
	}
	static void restore() {
		int bNum = dStack.pop();
		if(cursor >= bNum) cursor++;
	}
}

'Dot Algo∙ DS > PS' 카테고리의 다른 글

[프로그래머스] 2021 카카오 인턴 #5 시험장 나누기 (Java) (0)	2021.07.25
[프로그래머스] 2021 카카오 인턴 #4 미로 탈출 (Java) (0)	2021.07.21
[프로그래머스] 2021 카카오 인턴 #2 거리두기 확인하기 (Java) (0)	2021.07.18
[프로그래머스] 2021 카카오 인턴 #1 숫자 문자열과 영단어 (Java) (0)	2021.07.17
[BOJ] 백준 1854번 K번째 최단경로 찾기 (Java) (0)	2021.07.16

일	월	화	수	목	금	토
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

그릿 속의 해빗

[프로그래머스] 2021 카카오 인턴 #3 표 편집 (Java)

#3 표 편집

문제

제한사항

문제 풀이

구현

양방향 ListNode 풀이 코드

단순 풀이 코드

'Dot Algo∙ DS > PS' 카테고리의 다른 글

티스토리툴바

티스토리툴바

[프로그래머스] 2021 카카오 인턴 #3 표 편집 (Java)

#3 표 편집

문제

제한사항

문제 풀이

구현

양방향 ListNode 풀이 코드

단순 풀이 코드

'Dot Algo∙ DS > PS' 카테고리의 다른 글

'Dot Algo∙ DS/PS' 관련글

티스토리툴바

티스토리툴바