#1991 트리 순회
난이도 : 실버 1
유형 : 트리
1991번: 트리 순회
첫째 줄에는 이진 트리의 노드의 개수 N(1≤N≤26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 영문자
www.acmicpc.net
▸ 문제
이진 트리를 입력받아 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)한 결과를 출력하는 프로그램을 작성하시오.

예를 들어 위와 같은 이진 트리가 입력되면,
- 전위 순회한 결과 : ABDCEFG // (루트) (왼쪽 자식) (오른쪽 자식)
- 중위 순회한 결과 : DBAECFG // (왼쪽 자식) (루트) (오른쪽 자식)
- 후위 순회한 결과 : DBEGFCA // (왼쪽 자식) (오른쪽 자식) (루트)
▸ 입력
첫째 줄에는 이진 트리의 노드의 개수 N(1≤N≤26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 영문자 대문자로 매겨지며, 항상 A가 루트 노드가 된다. 자식 노드가 없는 경우에는 .으로 표현된다.
▸ 출력
첫째 줄에 전위 순회, 둘째 줄에 중위 순회, 셋째 줄에 후위 순회한 결과를 출력한다. 각 줄에 N개의 알파벳을 공백 없이 출력하면 된다.
문제 풀이
기본적인 트리 순회 문제이다. 연결리스트와 재귀함수를 사용하여 전위, 중위, 후위 순회를 돌 수 있다.
구상
- 문자열 데이터를 정수형으로 변환한 다음 연결리스트로 트리 구조를 구현해준다.
- 재귀를 통해 트리를 순회하며 다시 리턴될 때 각 탐색에 맞게 root값을 출력해준다.
전위 순회 (preorder)
root → left → right
전위 순회는 왼쪽, 오른쪽 자식노드를 탐색을 하기전에 root노드를 출력해준다.
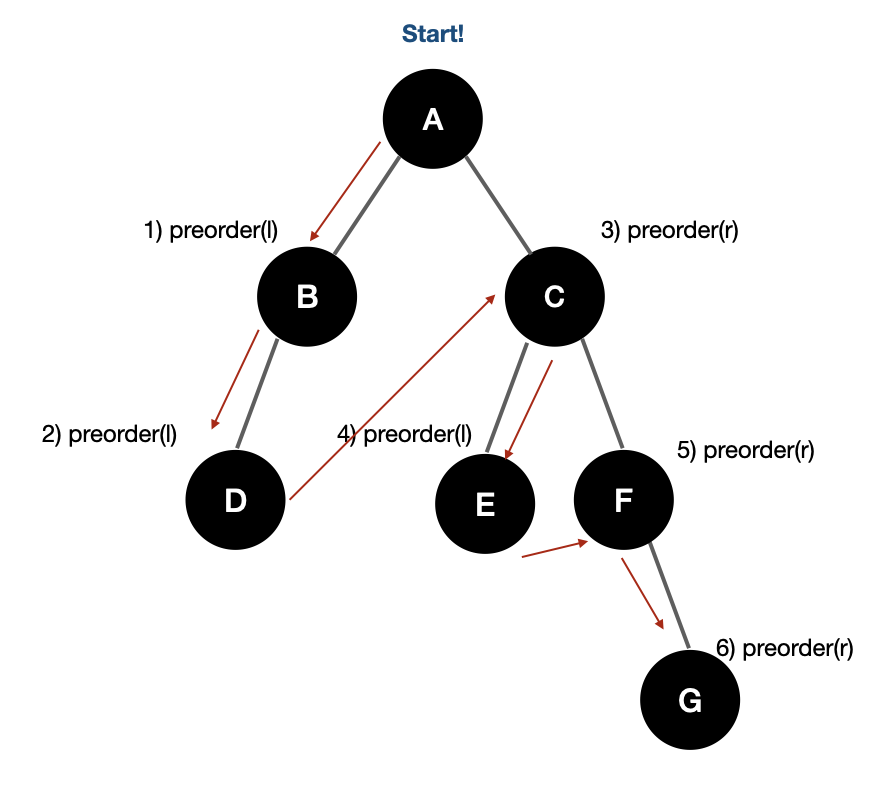
ex)
1) preorder(l)을 수행하기 전 root노드 "A" 출력
2) preorder(l)을 수행하기 전 root노드 "B" 출력
"D"는 leaf노드이므로 탐색없이 "D" 출력
...
결과 : ABDCEFG
중위 순회 (inorder)
left → root → right
중위 순회는 왼쪽노드를 탐색 후 오른쪽 자식노드를 탐색을 하기전에 root노드를 출력해준다.

ex)
1) inorder(l) → 2) inorder(l)을 수행하고 더 이상 왼쪽노드가 없으므로 차례대로 "D", "B", "A" 출력
3) inorder(r) → 4) preorder(l) 을 수행 후 더 이상 왼쪽노드가 없으므로 "E" 출력
...
결과 : DBAECFG
후위 순회
left → right → root
후위 순회는 왼쪽, 오른쪽노드를 모두 탐색 후 root노드를 출력해준다.

ex)
1) inorder(l) → 2) inorder(l)을 수행하고 더 이상 왼쪽노드가 없으므로 차례대로 "D", "B" 출력
그런 다음 루트노드는 건너뛰고 오른쪽 노드를 탐색
3) inorder(r) → 4) preorder(l) 을 수행 후 더 이상 왼쪽노드가 없으므로 "E" 출력
5) inorder(r) → 6) preorder(l) 을 수행 후 더 이상 탐색할 노드 없으므로 차례대로 "G", "F", "C" 출력
그리고 마지막으로 루트노드 "A" 출력
결과 : DBEGFCA
풀이 코드
import java.io.*;
import java.util.*;
public class Main {
static class Node {
int left;
int right;
public Node(int left, int right) {
this.left = left;
this.right = right;
}
}
static List<Node>[] list;
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = null;
int n = Integer.parseInt(br.readLine());
list = new ArrayList[n+1];
for(int i=1; i<n+1; i++) {
list[i] = new ArrayList<>();
}
for(int i=1; i<n+1; i++) {
String[] line = br.readLine().split(" ");
int data = line[0].charAt(0) -'A'+1;
int left = line[1].charAt(0) -'A'+1;
int right = line[2].charAt(0) -'A'+1;
list[data].add(new Node(left, right));
}
preorder(1);
sb.append("\n");
inorder(1);
sb.append("\n");
postorder(1);
System.out.println(sb.toString());
}
// 전위 순회 root > left > right
static void preorder(int start) {
for(Node node : list[start]) {
int l = node.left;
int r = node.right;
sb.append((char)(start+'A'-1));
if(l != -18) preorder(l);
if(r != -18) preorder(r);
}
}
// 중위 순회 left > root > right
static void inorder(int start) {
for(Node node : list[start]) {
int l = node.left;
int r = node.right;
if(l != -18) inorder(l);
sb.append((char)(start+'A'-1));
if(r != -18) inorder(r);
}
}
// 후위 순회 left > right > root
static void postorder(int start) {
for(Node node : list[start]) {
int l = node.left;
int r = node.right;
if(l != -18) postorder(l);
if(r != -18) postorder(r);
sb.append((char)(start+'A'-1));
}
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 2504번 괄호의 값 (Java) (0) | 2021.07.26 |
|---|---|
| [BOJ] 백준 2263번 트리의 순회 (Java) (2) | 2021.07.25 |
| [BOJ] 백준 1194번 달이 차오른다, 가자 (Java) (0) | 2021.07.25 |
| [BOJ] 백준 1062번 가르침 (Java) (0) | 2021.07.25 |
| [프로그래머스] 2021 카카오 인턴 #5 시험장 나누기 (Java) (0) | 2021.07.25 |




