#5 길 찾기 게임
난이도 : LEVEL 3
유형 : 트리
코딩테스트 연습 - 길 찾기 게임
[[5,3],[11,5],[13,3],[3,5],[6,1],[1,3],[8,6],[7,2],[2,2]] [[7,4,6,9,1,8,5,2,3],[9,6,5,8,1,4,3,2,7]]
programmers.co.kr
▸ 문제
전무로 승진한 라이언은 기분이 너무 좋아 프렌즈를 이끌고 특별 휴가를 가기로 했다.
내친김에 여행 계획까지 구상하던 라이언은 재미있는 게임을 생각해냈고 역시 전무로 승진할만한 인재라고 스스로에게 감탄했다.
라이언이 구상한(그리고 아마도 라이언만 즐거울만한) 게임은, 카카오 프렌즈를 두 팀으로 나누고, 각 팀이 같은 곳을 다른 순서로 방문하도록 해서 먼저 순회를 마친 팀이 승리하는 것이다.
그냥 지도를 주고 게임을 시작하면 재미가 덜해지므로, 라이언은 방문할 곳의 2차원 좌표 값을 구하고 각 장소를 이진트리의 노드가 되도록 구성한 후, 순회 방법을 힌트로 주어 각 팀이 스스로 경로를 찾도록 할 계획이다.
라이언은 아래와 같은 특별한 규칙으로 트리 노드들을 구성한다.
- 트리를 구성하는 모든 노드의 x, y 좌표 값은 정수이다.
- 모든 노드는 서로 다른 x값을 가진다.
- 같은 레벨(level)에 있는 노드는 같은 y 좌표를 가진다.
- 자식 노드의 y 값은 항상 부모 노드보다 작다.
- 임의의 노드 V의 왼쪽 서브 트리(left subtree)에 있는 모든 노드의 x값은 V의 x값보다 작다.
- 임의의 노드 V의 오른쪽 서브 트리(right subtree)에 있는 모든 노드의 x값은 V의 x값보다 크다.
아래 예시를 확인해보자.
라이언의 규칙에 맞게 이진트리의 노드만 좌표 평면에 그리면 다음과 같다. (이진트리의 각 노드에는 1부터 N까지 순서대로 번호가 붙어있다.)

이제, 노드를 잇는 간선(edge)을 모두 그리면 아래와 같은 모양이 된다.

위 이진트리에서 전위 순회(preorder), 후위 순회(postorder)를 한 결과는 다음과 같고, 이것은 각 팀이 방문해야 할 순서를 의미한다.
- 전위 순회 : 7, 4, 6, 9, 1, 8, 5, 2, 3
- 후위 순회 : 9, 6, 5, 8, 1, 4, 3, 2, 7
다행히 두 팀 모두 머리를 모아 분석한 끝에 라이언의 의도를 간신히 알아차렸다.
그러나 여전히 문제는 남아있다. 노드의 수가 예시처럼 적다면 쉽게 해결할 수 있겠지만, 예상대로 라이언은 그렇게 할 생각이 전혀 없었다.
이제 당신이 나설 때가 되었다.
곤경에 빠진 카카오 프렌즈를 위해 이진트리를 구성하는 노드들의 좌표가 담긴 배열 nodeinfo가 매개변수로 주어질 때,
노드들로 구성된 이진트리를 전위 순회, 후위 순회한 결과를 2차원 배열에 순서대로 담아 return 하도록 solution 함수를 완성하자.
▸ 제한사항
- nodeinfo는 이진트리를 구성하는 각 노드의 좌표가 1번 노드부터 순서대로 들어있는 2차원 배열이다.
- nodeinfo의 길이는 1 이상 10,000 이하이다.
- nodeinfo[i] 는 i + 1번 노드의 좌표이며, [x축 좌표, y축 좌표] 순으로 들어있다.
- 모든 노드의 좌표 값은 0 이상 100,000 이하인 정수이다.
- 트리의 깊이가 1,000 이하인 경우만 입력으로 주어진다.
- 모든 노드의 좌표는 문제에 주어진 규칙을 따르며, 잘못된 노드 위치가 주어지는 경우는 없다.
문제 풀이
트리 순회 응용 문제로 어려워보이지만 구상만 잘하면 술술 풀리는 문제이다.
구상
기존 데이터로 구할 수 있는 것은 루트 노드와 중위 순회이다. 왜냐하면 x축 좌표의 오름차순 대로 정렬한 순서가 중위 순회이고, 가장 높은 높이를 갖는 노드가 루트 노드이기 때문이다.
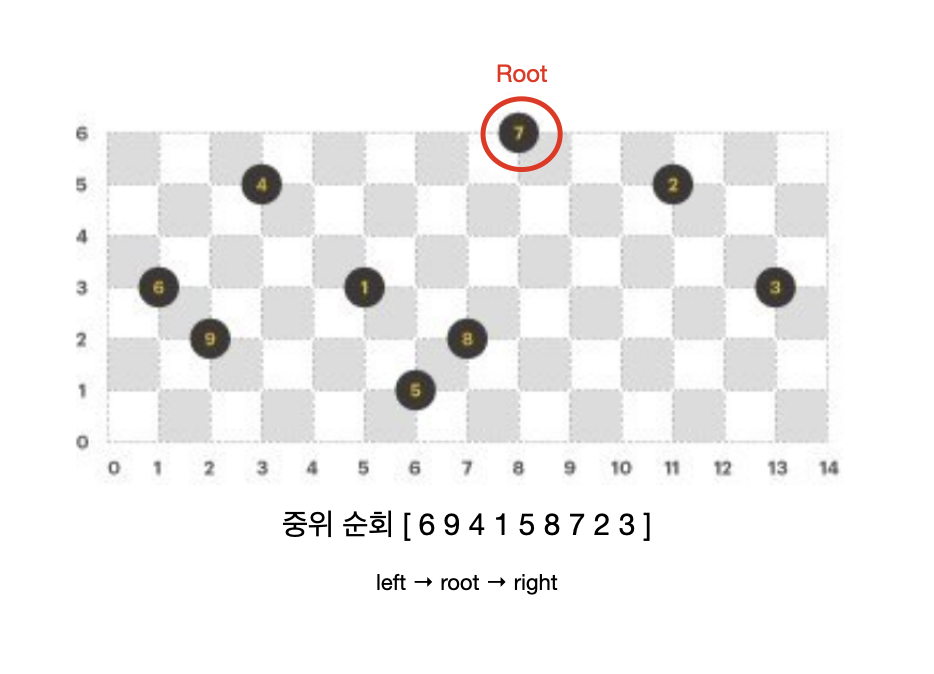
전위, 후위 순회가 이 문제에서 구해야 할 답이다. 이 순회는 사실 이진트리 구조(lefr-root-right)만 제대로 알고 있으면 쉽게 구할 수 있다.그러면 이 두 가지 데이터(루트노드, 중위 순회 순서)로 이진 트리의 구조를 파악할 수 있는 방법을 찾아야 한다.
조건에 따르면 x축과 높이로 왼쪽 노드인지 오른쪽 노드인지 쉽게 판별 할 수 있기 때문에 root노드를 기준으로 DFS로 각 왼쪽, 오른쪽 자식노드를 찾아준다. 위에서 말했다시피 중위 순회 데이터는 그냥 x죄표 데이터라고 보면 된다.
- 임의의 노드 V의 왼쪽 서브 트리(left subtree)에 있는 모든 노드의 x값은 V의 x값보다 작다.
- 임의의 노드 V의 오른쪽 서브 트리(right subtree)에 있는 모든 노드의 x값은 V의 x값보다 크다.
그렇게 구해준 이진트리 구조 데이터로 순회를 통해 전위, 후위 순회 순서를 뽑아주면 된다.
설계
- 노드의 데이터를 y좌표(높이)를 기준으로 내림차순 정렬해준다. Collections.sort(nodeData);
- 0번 데이터를 루트노드로 지정한다. (가장 높은 위치의 노드이므로)
- 이진트리 구조 데이터를 구해준다. (left - root - right)
- 높이를 기준으로 노드를 조회한다. if(nh == nodeData.get(nxt).y)
- 루트노드와 x좌표를 비교하여 왼쪽, 오른쪽 자식 노드를 파악한다. if(cur.x > child.x) ? left : right
- 각 높이에 해당하는 노드들을 탐색한 후에는 다음 단계의 높이의 노드들을 탐색해주면 된다. nh = nodeData.get(nxt).y;
- 이렇게 구한 이진트리 구조 데이터로 순회를 돌려 전위, 후위 순회 데이터를 구해준다. traversal(root);
풀이 코드
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Comparator;
class Solution {
static int preIdx =0, postIdx=0;
static int[][] gnode_info, answer;
static List<Node> nodeData;
static class Node implements Comparable<Node>{
int idx;
int x;
int y;
Node left;
Node right;
public Node(int idx, int x, int y){
this.idx = idx;
this.x = x;
this.y = y;
left = null;
right =null;
}
public void insertLeft(Node leafNode) {
this.left = leafNode;
}
public void insertRight(Node leafNode) {
this.right = leafNode;
}
@Override
public int compareTo(Node o) {
// TODO Auto-generated method stub
return o.y-this.y;
}
}
public int[][] solution(int[][] nodeinfo) {
int size = nodeinfo.length;
answer = new int[2][size];
gnode_info = nodeinfo;
nodeData = new ArrayList<>();
for(int i=1; i<size+1; i++) {
nodeData.add(new Node(i, nodeinfo[i-1][0], nodeinfo[i-1][1]));
}
Collections.sort(nodeData);
Node root = nodeData.get(0);
if(size>1) {
int nxt =1, nh =0;
outer : while(true) {
nh = nodeData.get(nxt).y;
while(true) {
if(nh == nodeData.get(nxt).y) { // 다음 탐색 높이
initNode(root, nodeData.get(nxt++));
}else break;
if(nxt > nodeData.size()-1) break outer;
}
}
}
traversal(root);
return answer;
}
static void traversal(Node cur) {
if(cur==null) return;
answer[0][preIdx++] = cur.idx; // 전위 순회
traversal(cur.left);
traversal(cur.right);
answer[1][postIdx++] = cur.idx; // 후위 순회
}
// 노드 데이터 초기화
static void initNode(Node cur, Node child) {
if(cur.x > child.x) {
if(cur.left == null ) {
cur.insertLeft(child);
}else {
initNode(cur.left, child);
}
}else {
if(cur.right == null ) {
cur.insertRight(child);
}else {
initNode(cur.right, child);
}
}
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [프로그래머스] 2019 카카오 블라인드 #7 블록 게임 (Java) (0) | 2021.09.01 |
|---|---|
| [프로그래머스] 2019 카카오 블라인드 #6 매칭 점수 (Java) (0) | 2021.09.01 |
| [프로그래머스] 2019 카카오 블라인드 #4 무지의 먹방 라이브 (Java) (0) | 2021.08.31 |
| [프로그래머스] 2019 카카오 블라인드 #3 후보키 (Java) (0) | 2021.08.30 |
| [프로그래머스] 2019 카카오 블라인드 #2 실패율 (Java) (0) | 2021.08.29 |




