#9250 문자열 집합 판별
난이도 : 플레 2
유형 : 문자열 탐색 / 트라이 / 아호-코라식
9250번: 문자열 집합 판별
집합 S는 크기가 N이고, 원소가 문자열인 집합이다. Q개의 문자열이 주어졌을 때, 각 문자열의 부분 문자열이 집합 S에 있는지 판별하는 프로그램을 작성하시오. 문자열의 여러 부분 문자열 중 하
www.acmicpc.net
▸ 문제
집합 S는 크기가 N이고, 원소가 문자열인 집합이다. Q개의 문자열이 주어졌을 때, 각 문자열의 부분 문자열이 집합 S에 있는지 판별하는 프로그램을 작성하시오. 문자열의 여러 부분 문자열 중 하나라도 집합 S에 있으면 'YES'를 출력하고, 아무것도 없으면 'NO'를 출력한다.
예를 들어, 집합 S = {"www","woo","jun"} 일 때, "myungwoo"의 부분 문자열인 "woo" 가 집합 S에 있으므로 답은 'YES'이고, "hongjun"의 부분 문자열 "jun"이 집합 S에 있으므로 답은 'YES'이다. 하지만, "dooho"는 모든 부분 문자열이 집합 S에 없기 때문에 답은 'NO'이다.
▸ 입력
첫째 줄에 집합 S의 크기 N이 주어진다. (1 ≤ N ≤ 1000)
다음 N개 줄에 집합 S의 원소들이 주어진다. 이 문자열의 길이는 100을 넘지 않는다.
다음 줄에 답을 판별해야 하는 문자열의 개수 Q가 주어진다. (1 ≤ Q ≤ 1000)
다음 Q개 줄에 답을 판별해야 하는 문자열이 주어진다. 이 문자열의 길이는 10000을 넘지 않는다.
입력으로 주어지는 모든 문자열은 알파벳 소문자로만 이루어져 있다.
▸ 출력
Q개 줄에 각 문자열에 대한 답을 출력한다.
문제 풀이
해당 문제는 다중 문자열 탐색 문제이다.
- p 패턴 수 : 1,000개
- m 모든 패턴들의 길이합 : 100,000
- n 크기 : 10,000
KMP 알고리즘으로 풀이할 경우 하나의 문자열을 판별할 경우에 최악의 경우 O(m + p*n) 대략 10억정도의 시간이 걸린다. 그래서 이는 KMP 알고리즘과 트라이(Trie) 자료구조를 접목시킨 아호-코라식(Aho-Corasick) 알고리즘을 사용해야 한다.
💡 아호-코라식(Aho-Corasick) 알고리즘에 대한 설명은 여기를 참고해주세요.
아호-코라식 알고리즘을 사용하면 O(n+m+p)의 시간복잡도로 해결이 가능하다. 아호-코라식 알고리즘을 간략하게 설명하면 트라이 자료구조를 사용해서 실패 링크와 출력 문자열 목록을 생성한 다음 KMP 알고리즘과 같은 방식으로 매칭 문자열을 탐색해주면 된다.
해당 예제를 통해 트라이 상에서 계산한 실패함수 자료구조를 구현하면 다음과 같다.
- 실선 화살표는 해당 상태에서 대응이 성공했을 경우 움직일 수 있는 상태이다.
- 점선 화살표는 실패 함수를 나타낸다. KMP로 따지면 부분 일치 테이블과 같은 역할을 한다고 보면 된다.
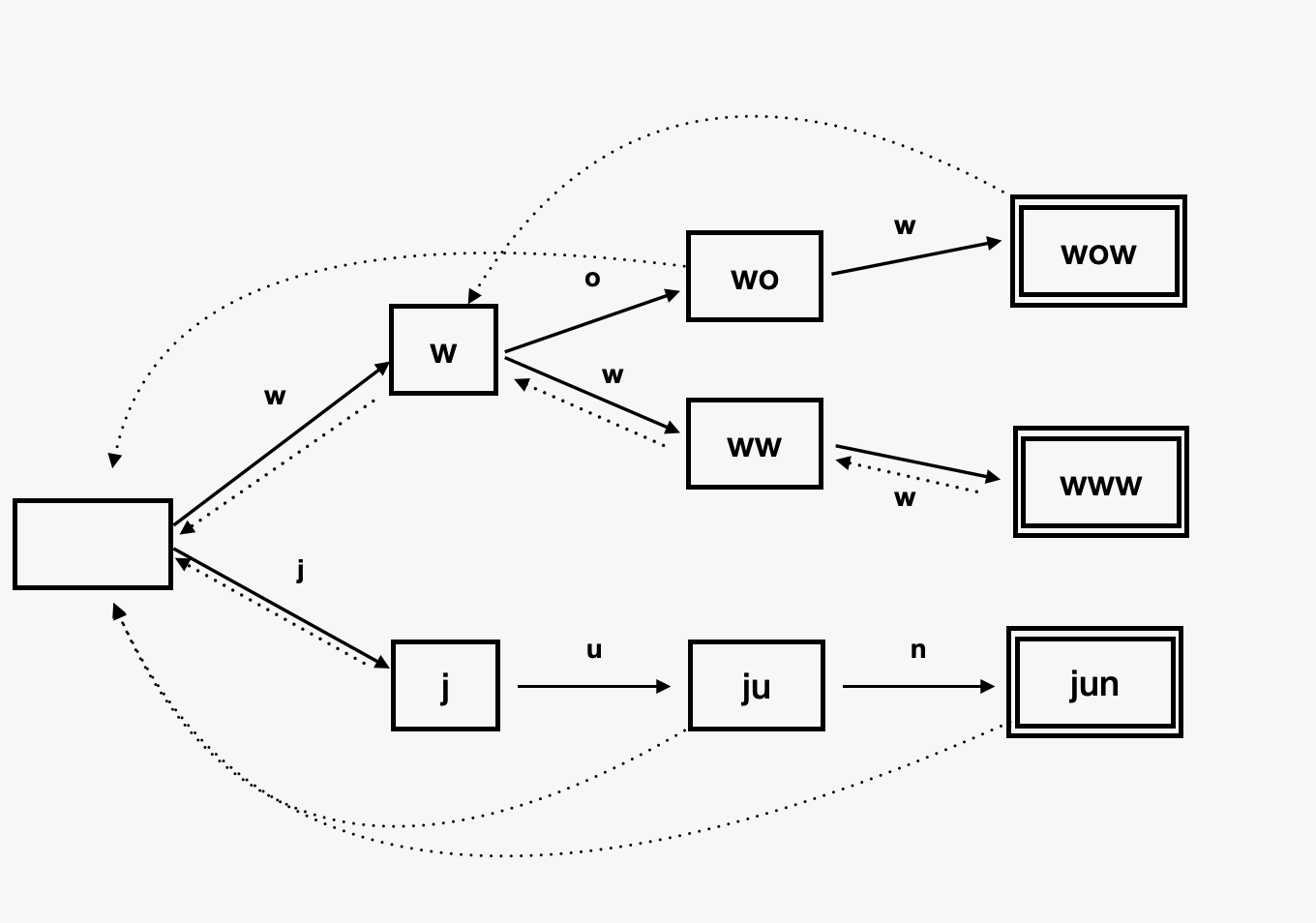
설계
- 트라이(Trie) 자료구조를 구현한다.
- 기존 트라이 자료구조에서 실패링크를 추가한다.
- 실패 링크를 계산하는 로직을 추가한다.
- 탐색 문자열(word)와 매칭시키는 KMP 알고리즘을 구현한다.
- 몇 글자나 대응되었는지를 나타내는 matched 변수 → 현재 상태를 나타내는 trieNode
- 부분 일치 테이블 참조 대신 → 실패 링크를 참조
- 주어지는 pattern을 트라이 자료구조에 저장한다. insert(br.readLine());
- 실패함수를 계산해준다. computeFailFunc()
- 판별해야 하는 문자열이 매칭되면 "YES" 아니면 "NO"를 출력한다. ahoCorasick(String word)
풀이 코드
import java.io.*;
import java.util.*;
public class Main {
static final int SIZE = 26;
static class TrieNode{
boolean output;
Map<Character, TrieNode> child = new HashMap<>();
TrieNode fail;
public TrieNode() {}
public void insert(String word) {
TrieNode curNode = this;
for(int i=0; i<word.length(); i++) {
char c = word.charAt(i);
curNode.child.putIfAbsent(c, new TrieNode());
curNode = curNode.child.get(c);
if(i== word.length()-1) {
curNode.output = true;
}
}
}
public void computeFailFunc() {
Queue<TrieNode> q = new LinkedList<>();
this.fail = this;
q.add(this);
while(!q.isEmpty()) {
TrieNode cur = q.poll();
for(int i=0; i<SIZE; i++) {
char c = (char)(i+97);
// cur -> nxt
TrieNode nxt = cur.child.get(c);
if(nxt ==null) continue;
// 1레벨 노드의 실패 연결은 항상 루트
if(cur == this) {
nxt.fail = this;
}else { //아닌 경우 부모의 실패 연결을 따라가면서 실패 연결을 찾는다.
TrieNode failLinkNode = cur.fail;
while(failLinkNode!=this && failLinkNode.child.get(c) == null) {
failLinkNode = failLinkNode.fail;
}
if(failLinkNode.child.get(c) != null) {
failLinkNode = failLinkNode.child.get(c);
}
nxt.fail = failLinkNode;
}
// 이 위치에서 끝나는 바늘 문자열이 있으면 추가한다.
if(nxt.fail.output) {
nxt.output =true;
}
q.add(nxt);
}
}
}
public boolean ahoCorasick(String word) {
TrieNode curNode = this;
for(int i=0; i<word.length(); i++) {
char c = word.charAt(i);
while(curNode != this && curNode.child.get(c) ==null) {
curNode = curNode.fail;
}
if(curNode.child.get(c)!=null) {
curNode = curNode.child.get(c);
}
if(curNode.output) {
return true;
}
}
return false;
}
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
TrieNode trieSet = new TrieNode();
for(int i=0; i<n; i++) {
trieSet.insert(br.readLine());
}
trieSet.computeFailFunc();
StringBuilder sb = new StringBuilder();
int q = Integer.parseInt(br.readLine());
for(int i=0; i<q; i++) {
if(trieSet.ahoCorasick(br.readLine())) {
sb.append("YES\n");
}else {
sb.append("NO\n");
}
}
System.out.println(sb.toString());
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 10256번 돌연변이 (Java) (0) | 2021.12.01 |
|---|---|
| [BOJ] 백준 3197번 백조의 호수 (Java) (0) | 2021.11.30 |
| [BOJ] 백준 2887번 행성 터널 (Java) (0) | 2021.11.28 |
| [BOJ] 백준 2660번 회장뽑기 (Java) (0) | 2021.11.27 |
| [BOJ] 백준 9328번 열쇠 (Java) (0) | 2021.11.26 |




