아호 코라식(Aho-Corasick) 알고리즘
아호 코라식 알고리즘(Aho–Corasick string matching algorithm)은 Alfred V. Aho와 Margaret J. Corasick이 고안한 문자열 검색 알고리즘(매칭 알고리즘)이다. (위키 참고)
패턴 1개를 탐색하는 매칭 알고리즘은 선형 시간에 구현됨을 KMP 등 여러 알고리즘을 통하여 증명되었다. 하지만 패턴 집합에 대하여 이러한 알고리즘을 수행하게 되면 패턴 개수에 비례하여 그 속도가 느려지게 된다.
- m = 모든 패턴들의 길이 합, p = 패턴수, n = text 크기
- 즉 , O(m + p*n)의 시간 복잡도를 가지게 된다.
- 하지만 아호 코라식 알고리즘을 이용하면 O (m + p + n)의 시간복잡도로 패턴 집하에 대하여 패턴 길이와 텍스트의 선형 시간 탐색에 처리할 수 있게 된다. 이에 대한 분석은 모든 구현을 마친뒤 마지막에 한 번 더 다룰 것이다.
다중 문자열 검색
여러 패턴 집합을 구하는 문제를 다중 문자열 검색 문제라고 한다.
- KMP는 1개 패턴 문자열을 매칭 시키는 문제를 해결했다면
- 다중 문자열 검색은 짚더미(parent): "CACACHEFCACHY", 바늘 문자열(pattern[]): {"CACHE", "HE", "CHEF", "ACHY"} 이 있다고 하면 각 바늘 문자열들의 출현 위치를 모두 찾아 해결해야 한다.
- KMP 알고리즘을 사용하면 위에서 말했던 바와 같이 패턴 수(바늘 문자열 갯수)만큼 순회해야 한다.
1. KMP 알고리즘으로 접근하기
KMP 알고리즘의 동작원리를 돌이켜 보자. KMP 알고리즘은 전처리 과정에서 부분 매칭 테이블을 계산하는데, 이것은 바늘 문자열(pattern)의 각 접두사마다 이 접두사의 접두사도 되고 접미사도 되는 문자열의 최대 길이를 계산해 둔 것이다.
- 예를 들어 "CACHE"를 찾는데 첫 세 글자인 "CAC가 대응되고 실패했다고 하자. 이때 대응된 부분의 접두사도 되고 접미사도 되는 최대 문자열은 "C"이다.
- 따라서 KMP 알고리즘은 세 글자 대신 한 글자가 대응되었다고 생각하고 다음 글자가 A인지를 확인한다. 이와 같은 과정이 있기 때문에 "CACACHE" 같은 문자열에서 "CACHE"를 찾을 때에도 parent의 각 문자를 한 번만 보고 모든 출현 위치를 찾아낼 수 있다.
- 대응에 실패했을 때 어디로 가서 검색을 계속해야 할지 알려준다는 의미에서 이와 같은 정보를 실패 함수(failure function)라고도 부른다.
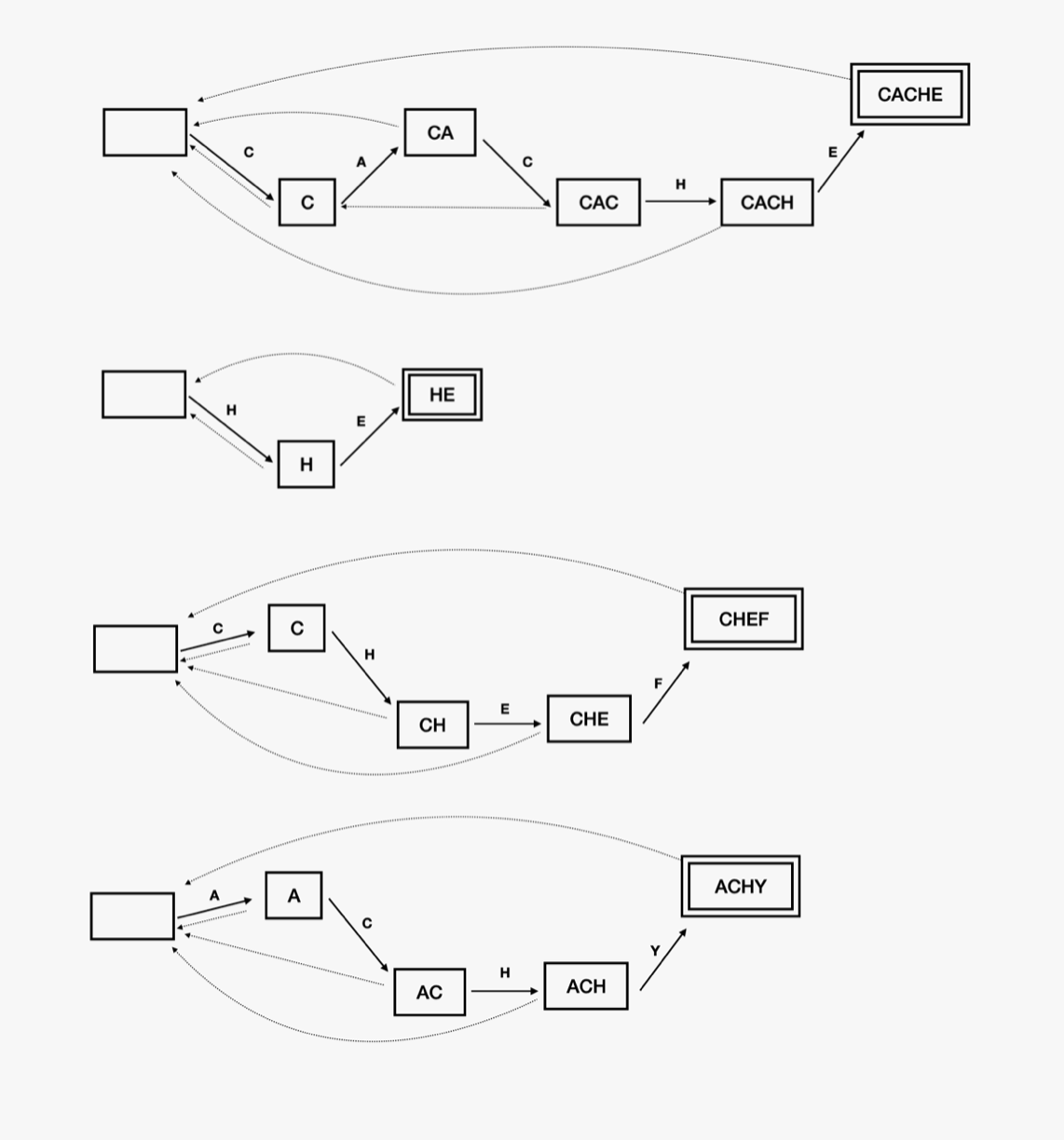
바늘 문자열(pattern)의 실패 함수 정보를 그림으로 표현해보자. "CACHE", "HE", "CHEF", "ACHY"에 대해 KMP 알고리즘이 생성하는 실패 함수 정보를 나타낸다.
- 오른쪽으로 가는 실선 화살표는 해당 상태에서 대응이 성공했을 경우 움직일 상태를 의미하고,
- 왼쪽으로 가는 점선 화살표는 실패 함수를 나타낸다.
- 예를 들어 "CAC"상태에 있는 다음 글자가 H라면 "CACH" 상태로 갈 수 있지만, 해당 글자가 H가 아니라면 "C"로 돌아가 다음 글자가 A인지 비교해야 한다.
[KMP 알고리즘의 전처리 결과 시뮬레이션]
2. 트라이(Trie) 자료구조 적용하기
트라이는 집합에 포함된 문자열을 찾는 탐색 자료 구조이다. 트라이에 포함된 문자열들이 접두사를 공유할 경우, 이 접두사들은 같은 노드에 대응된다는 점을 이용해 탐색 공간을 줄이는 알고리즘을 설계할 수 있다.
- 위 그림의 문제점은 중복된 데이터가 너무 많다는 것이다. 이 모든 접두사들을 트라이로 그려보면 다음 그림과 같은 자료구조를 얻을 수 있다. 겹치던 상태들이 깨끗하게 정리되었다.
[문제에서 찾는 패턴을 모두 포함하는 트라이]

실패 함수를 다음과 같이 다시 정의하자.
- failure(s) = s 의 접미사이면서 트라이에 포함된 가장 긴 문자열까지 가는 화살표
이와 같은 정의를 이용해 위의 트라이 자료구조 그림에서 각 노드의 실패 함수를 계산하면 다음 그림과 같은 상태로 나아간다. 이와 같은 실패 함수를 전처리 과정에서 만든 뒤, 짚더미 문자열(parent)의 글자를 순회하면서 트라이의 상태들을 서로 오가면 모든 바늘 문자열들에 대해 동시에 KMP 알고리즘을 수행하는 것과 같은 효과를 얻을 수 있다.
[트라이 상에서 계산한 실패 함수]
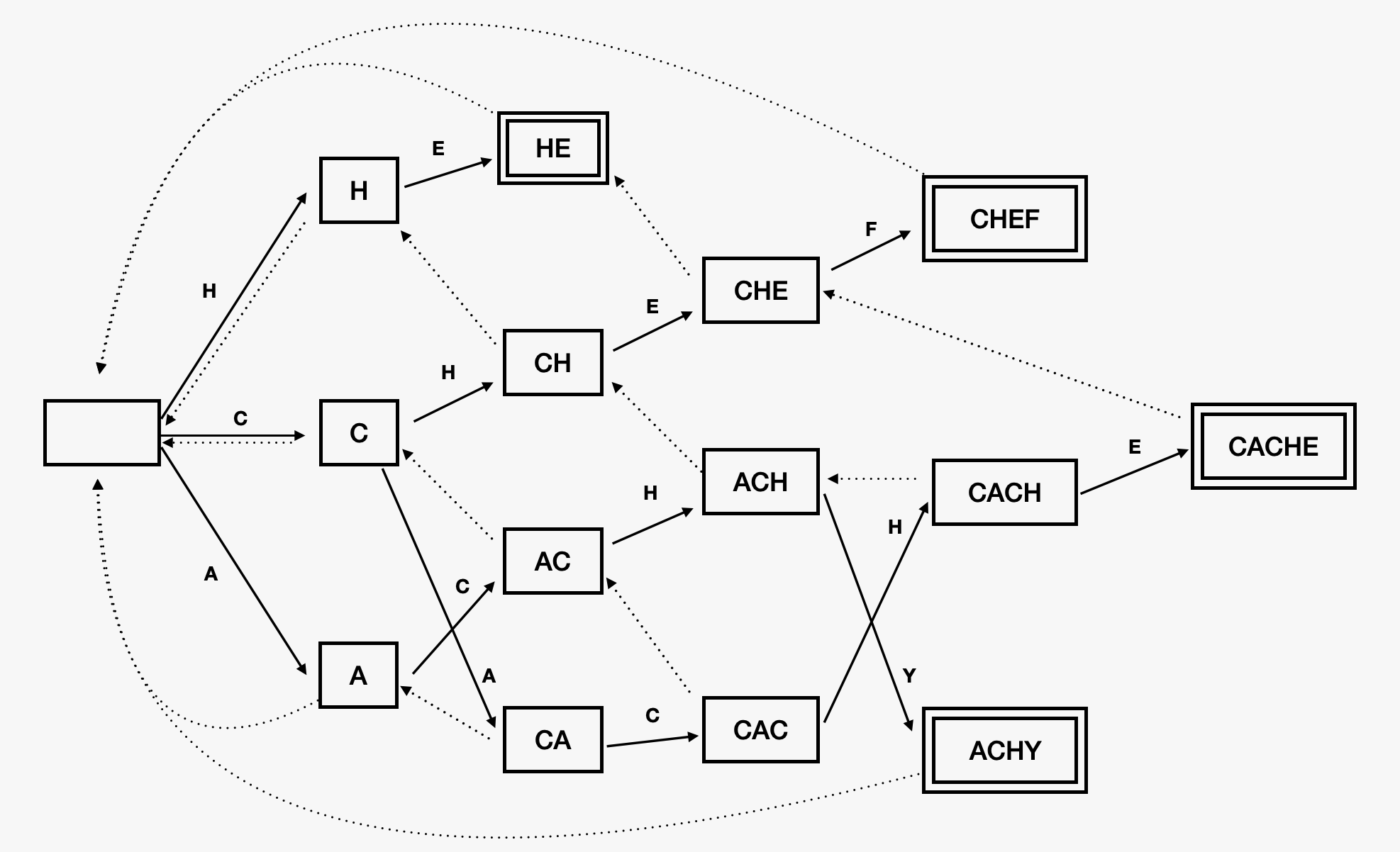
이 알고리즘을 바로 아호-코라식(Aho-Corasick) 문자열 검색 알고리즘이라고 부른다. 아호-코라식 알고리즘은 긴 문서에서 많은 문자열을 동시에 찾아야 하는 검색 엔진 등에서 특히 유용하게 사용된다. 이제 아호-코라식 알고리즘이 실패 함수를 계산하는 방법과 실제 문자열을 탐색하는 과정을 구현해보자.
- 따라서, 아호-코라식 알고리즘은 (1)패턴 1개를 탐색하는 문자열 매칭 알고리즘에 (2)집합에 포함된 문자열을 탐색하는 자료구조를 합성한 것이라고 보면 된다.
아호-코라식(Aho-Corasick) 문자열 검색 알고리즘 구현하기
1. 실패 함수의 계산
아호-코라식 알고리즘을 사용하기 위해서는 트라이 자료구조에서 다음과 같은 정보를 추가적으로 가지고 있어야 한다.
- 실패 링크(failure link)는 이 노드에서의 실패 함수 값으로, 이 노드에서 다음 글자가 대응하는 데 실패했을 때 다음으로 가서 시도해야 할 노드의 포인터이다. 위 그림에서 점선 화살표들이 실패 링크를 나타낸다.
- 출력 문자열 목록은 각 노드에 도달했을 때 어떤 바늘 문자열(pattern)들을 발견하게 되는지를 저장한다.
- 한 바늘 문자열(pattern)이 다른 바늘 문자열의 부분 문자열인 경우, 해당 바늘 문자열이 종료되는 노드 외의 장소에서도 문자열을 발견할 수 있기 때문에 별도의 목록이 필요하다.
- 예를 들어 세 개의 바늘 문자열 ABC, B, BC가 있다면 상태 AB에 도달했을 때는 바늘 문자열 B를, 상태 ABC에 도달했을 때는 바늘 문자열 ABC와 BC를 발견할 수 있다.
2. 실패 링크 만들기
출력 문자열 목록은 실패 링크가 있을 경우 쉽게 계산할 수 있으므로, 우선은 각 노드의 실패 링크를 형성하는데 집중하자.
- 주어진 트라이 노드의 실패 링크를 계산하는 가장 간단한 방법은 해당 노드에 대응된 문자열의 모든 접미사들을 하나하나 시도하면서 이 중 트라이에 포함되어 있는 첫 번째 문자열을 찾는 것이다.
- 이 방식은 아주 비효율적이지만 트라이 크기가 그리 크지 않다면 써먹을 수는 있다.
모든 접미사들을 시도하는 방법보다 더 효율적인 방식이 있으니 이를 공부해보자.
2-1. 부모 노드의 실패 링크를 이용해 자식 노드의 실패 링크를 쉽게 알아내기
보다 빠르게 실패 링크를 계산하는 중요한 단서는 부모 노드의 실패 링크를 이용해 자식 노드의 실패 링크를 쉽게 알아낼 수 있다는 것이다. "CAC"와 "CACH"를 예로 들어보자. 두 노드의 실패 링크인 "AC"와 "ACH"또한 서로 부모의 자손 사이임을 알 수있다. 왜?
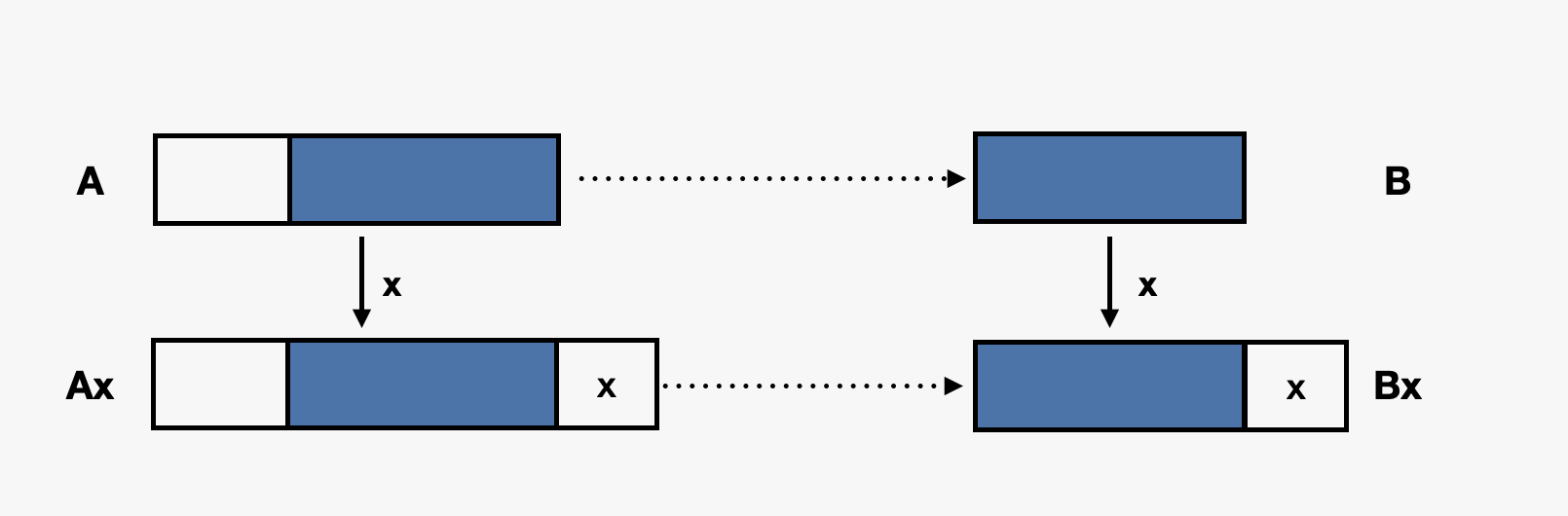
어떤 문자열 A와 그 뒤에 글자 x를 붙인 문자열 Ax가 트라이 상에서 부모 자식 관계라 하자.
- Ax의 실패 링크가 루트로 가지 않는 경우, 실패 링크를 따라가 만나는 문자열의 마지막 문자는 항상 x이다. 따라서 실패 링크를 따라가 만나는 문자열의 마지막 문자는 항상 x이다. 따라서 실패 링크를 따라가 만나는 문자열의 마지막 문자는 항상 x이다.
- 따라서 실패 링크를 따라가 만난 문자열을 Bx라고 쓸 수 있다. 여기서 x를 떼어낸 B를 생각해 보면 그림에서 볼 수 있듯이 B는 항상 A의 접미사가 되어야 한다.
- 따라서 부모 노드인 A의 실패 연결에 B에 x를 붙인 자손 Bx가 있는지를 확인해 Bx가 Ax의 실패 링크가 됨을 쉽게 알 수 있다.
2-2. 부모 노드의 실패 링크로 찾을 수 없을 경우 부모의 부모의 실패링크를 계속해서 탐색하기
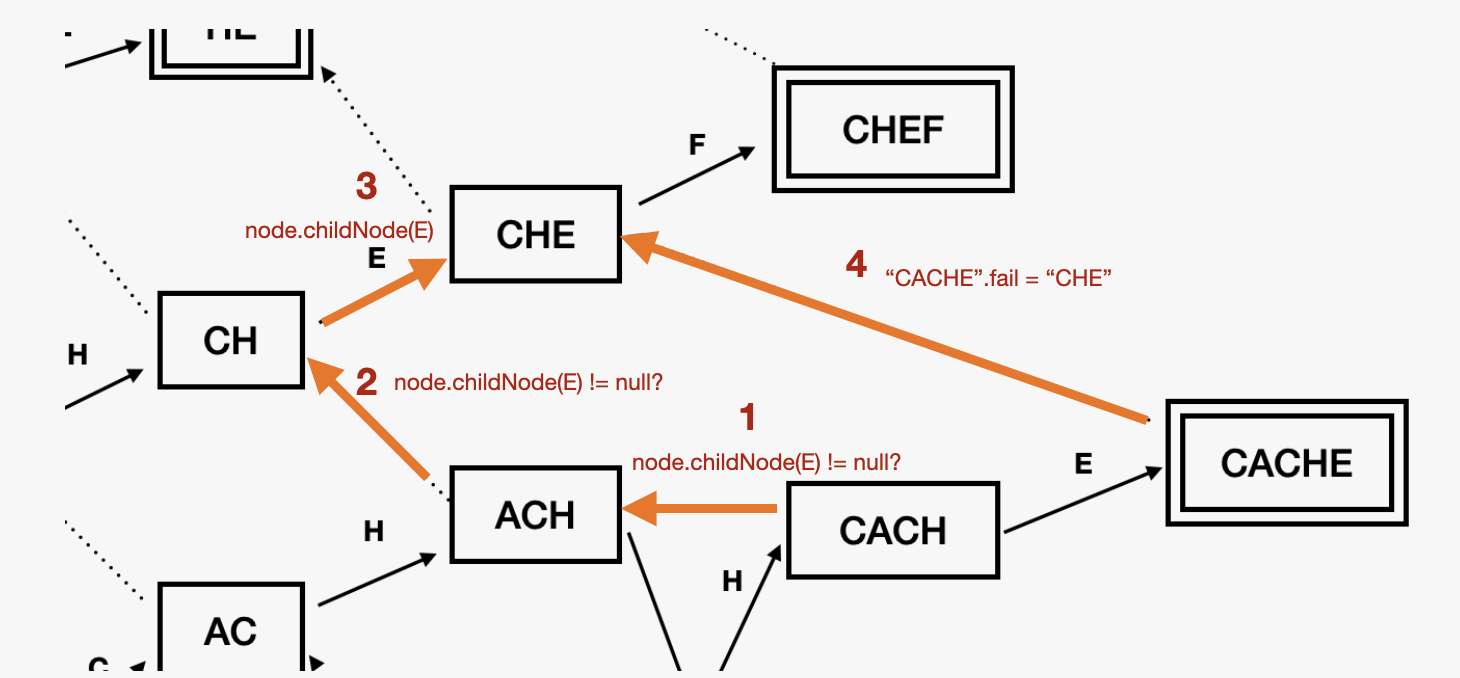
물론 1번 규칙만으로 모든 실패 링크를 찾을 수 없다. "CACH"와 "CACHE"의 관계를 살펴보자.
- "CACH"의 실패 링크인 "ACH"에는 E로 표시된 간선이 없기 때문에 이 규칙으로는 "CACHE"의 실패 연결을 찾을 수 없다.
- 이때 우리가 할 일은 "ACH"의 실패 링크를 한 번 더 따라가는 것이다. 이렇게 실패 링크를 따라가면 "CACH"의 접미사들을 긴 것부터 순회하게 된다.
- 이 과정에서 처음으로 E로 표시된 간선이 있는 노드는 "CH"이므로, 이 간선을 따라가서 "CHE"를 얻으면 된다. 만약 실패 연결을 따라 루트로 돌아갈 때까지 다음 글자로 표시된 간선을 찾을 수 없다면 이 노드의 실패 링크는 트라이의 루트가 된다.
이제 마지막으로 실패 링크를 계산할 순서를 설계하면 된다. 한 노드의 실패 링크를 계산하기 위해서는 그 부모 노드에서 실패 링크를 따라가 만날 수 있는 모든 노드들에 대해 실패 링크를 먼저 계산해야 하기 때문이다.
- 단순하게 재귀호출을 이용한 DFS로 트라이의 노드들을 순회하면서, 방문 순서대로 실패 연결을 계산해서는 이 조건을 만족시킬 수 없다.
- 이때 부모의 실패 연결은 알 수 있지만 부모에서 실패 링크를 따라간 노드의 실패 링크를 모를 수 있기 때문이다.
2-3. BFS 탐색 으로 구현하기
이 문제를 해결하는 방법은 실패 링크를 따라갔을 때 만나는 문자열은 원래 노드의 문자열보다 항상 짧다는 데 주목하는 것이다.
- 루트에서부터 시작해서 깊이가 낮은 노드들부터 순서대로 실패 링크를 계산하면, 항상 현재 노드보다 짧은 문자열을 갖는 모든 노드들에 대해 실패 링크를 계산한 뒤이기 때문에 우리에게 필요한 노드들의 실패 링크를 모두 가지고 있을 것이다.
- 따라서 실패 링크를 만드는 computeFailFunc()는 너비 우선 탐색인 BFS를 이용하여 구현한다.
public void computeFailFunc() {
Queue<TrieNode> q = new LinkedList<>();
this.fail = this; // this : root
q.add(this);
while(!q.isEmpty()) {
TrieNode cur = q.poll();
for(int i=0; i<26; i++) { // 알파벳만 포함되어있는 문자열 탐색이므로 26으로 설정
char c = (char)(i+97);
TrieNode nxt = cur.childNode.get(c);
if(nxt ==null) continue;
// 1레벨 노드의 실패 연결은 항상 루트
if(cur == this) {
nxt.fail = this;
}else { //아닌 경우 부모의 실패 연결을 따라가면서 실패 연결을 찾는다.
TrieNode t = cur.fail; // t: 부모 실패노드
// 2. 부모 실패노드의 자식노드가 c가 아닌 경우 실패노드 거슬러 탐색하기
while(t!=this && t.childNode.get(c) == null) {
t = t.fail;
}
// 1. 부모 실패노드의 자식노드가 c인 경우 실패링크 연결
if(t.childNode.get(c) != null) {
t = t.childNode.get(c);
}
nxt.fail = t;
}
// 이 위치에서 끝나는 바늘 문자열이 있으면 추가한다. (출력 링크)
if(nxt.fail.output) {
nxt.output =true;
}
q.add(nxt);
}
}
}
2-4. 출력 문자열 목록을 계산하는 부분 (output)
- 실패 링크를 계산하고 나면 해당 위치에서 출력 문자열 목록을 복사해 온 뒤, 현재 위치에서 끝나는 문자열을 추가한다.
- 이와 같은 방법으로 출력 문자열 목록을 계산할 수 있는 이유는, 현재 노드에 대응되는 문자열의 접미사가 트라이에 포함된 어떤 문자열과 같다면, 이 노드에서 실패 링크를 따라가다 보면 이 문자열을 반드시 찾을 수 있기 때문이다.
- "CACHE"에서 실패 링크를 따라가다 보면 "HE"를 찾을 수 있는 것처럼 말이다.
- 위 예제에서 주어진 그래프에는 "CHE"가 새롭게 출력 문자열 목록에 추가된다.

3. 실제 탐색 과정의 구현
이와 같이 실패 링크를 계산해 두고 나면 실제 탐색 과정은 KMP 알고리즘과 거의 다를 것이 없다.
- 몇 글자나 대응되었는지를 나타내는 matched 변수 → 현재 상태를 나타내는 trieNode로 바뀌고,
- 부분 일치 테이블 참조 대신 → 실패 링크를 참조한다.
public boolean ahoCorasick(String word) {
TrieNode trieNode = this;
// 짚더미 문자열 탐색 (0~word.length()-1)
for(int i=0; i<word.length(); i++) {
char c = word.charAt(i);
// 해당 노드가 루트가 아니고 해당 트리에는 더이상 일치하는 문자(c)가 없을 때 실패링크로 이동
while(trieNode != this && trieNode.childNode.get(c) ==null) {
trieNode = trieNode.fail;
}
// 해당되는 문자(c)가 트라이에 있다면 해당 노드로 이동
if(trieNode.childNode.get(c)!=null) {
trieNode = trieNode.childNode.get(c);
}
if(trieNode.output) {
return true; // 문자열 집합 중 해당되는 바늘 문자열이 있다면 true 반환
}
}
return false; // 해당되는 바늘 문자열이 없다면 false 반환
}
시간 복잡도 분석
아호-코라식 알고리즘은 KMP 알고리즘의 확장판이다 보니, 시간 복잡도 분석도 거의 비슷하게 할 수 있다.
ahoCorasick()의 시간 복잡도는 word의 글자들을 순회하는 for문 안에 들어 있는 반복문들에 의해 지배된다.
- 우선 출력 문자열 목록을 순회하는 for문은 짚더미에 바늘이 출현하는 횟수만큼 수행된다는 것을 알 수 있다.
- while문의 수행 시간은 KMP알고리즘과 비슷한 방식으로 분석할 수 있다. while문의 수행 과정에서 trieNode에 대응되는 문자열의 길이가 어떻게 변화하는지 생각해 보자. 이 길이는 짚더미(word)의 각 문자당 최대 1씩만 증가할 수 있다.
- 반면 실패 링크를 따라갈 때 마다 trieNode가 표현하는 문자열의 길이는 항상 1이상 줄어들며, 0 밑으로 내려갈 수 없다.
- 따라서 최악의 경우에도 실패 연결을 따라가는 횟수는 짚더미(word)의 길이 이하임을 알 수 있다.
- 결과적으로 이 두 반복문의 수행 횟수는 바늘(trieNode) 출현 횟수 P, 짚더미(parent)의 길이 N에 대해 O(N+P)가 된다.
computeFailFunc()는 계산하기 좀더 복잡하지만 비슷한 방법으로 분석할 수 있다.
- 해당 로직은 실패 링크를 따라가는 while문이 지배한다. 이 while문의 수행 횟수를 각 바늘 문자열에 포함되는 노드별로 나누어 분석해보자.
- 예를들어 "CACHE"를 트라이에 삽입하면 5개의 노드가 생겨난다. 이 5개의 노드에 대해 실패 링크를 계산하는 과정에서 while문의 내부가 총 몇 번이나 수행될까?
- t는 바늘의 각 글자를 처리할 때마다 최대 1칸씩 아래로 내려가므로 최대 다섯 번 아래로 내려갈 수 있다.
- 반면 while문의 내부가 수행될 때마다 t는 1칸 이상씩 올라가야 하므로, while문의 내부가 다섯 번 이상 수행될 수는 없다. 각 문자열에 대해 이것을 모두 더하면 결국 바늘 문자열 길이의 합 M에 선형 비례함을 알 수 있다.
따라서 전처리를 포함한 아호-코라식 알고리즘의 시간 복잡도는 O(N + M + P)이다.
슬라이드 참고 자료
시뮬레이션 과정과 아호-코라식 알고리즘 발전 과정 자세히 설명되어 있는 슬라이드 참고 자료
- KMP 매칭 알고리즘 p9 ~p39
- 다중 문자열 검색 아이디어 p41 ~ 54
- 문자열 집합을 탐색하는 트라이 자료구조 접목 p55 ~ p101
- 실패 링크 초기 모델 p102 ~ p190
- 실패 링크(= suffix link) p192 ~ p238
- 출력 링크 p239 ~ p269
아호-코라식 예제
※ 참고 자료
'Dot Algo∙ DS > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘] SCC(Strongly Connected Component) (백준 2150번 풀이) (0) | 2021.12.05 |
|---|---|
| [알고리즘] 단절점 (백준 11266번 풀이) (0) | 2021.12.03 |
| [알고리즘] 최적화 문제 결정 문제로 바꿔풀기 - 파라메트릭 서치(Parametric Search) (0) | 2021.10.22 |
| [알고리즘] 탐욕스러운 그리디(Greedy) 알고리즘 정리 (Java) (1) | 2021.10.19 |
| [알고리즘] 최장 공통 부분 수열 LCS - DP & 이진탐색 LIS (Java) (0) | 2021.08.10 |




