#2150 Strongly Connected Component
난이도 : 플레 5
유형 : 그래프 이론 / SCC
2150번: Strongly Connected Component
첫째 줄에 두 정수 V(1 ≤ V ≤ 10,000), E(1 ≤ E ≤ 100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정
www.acmicpc.net
▸ 문제
방향 그래프가 주어졌을 때, 그 그래프를 SCC들로 나누는 프로그램을 작성하시오.
방향 그래프의 SCC는 우선 정점의 최대 부분집합이며, 그 부분집합에 들어있는 서로 다른 임의의 두 정점 u, v에 대해서 u에서 v로 가는 경로와 v에서 u로 가는 경로가 모두 존재하는 경우를 말한다.

예를 들어 위와 같은 그림을 보자. 이 그래프에서 SCC들은 {a, b, e}, {c, d}, {f, g}, {h} 가 있다. 물론 h에서 h로 가는 간선이 없는 경우에도 {h}는 SCC를 이룬다.
▸ 입력
첫째 줄에 두 정수 V(1 ≤ V ≤ 10,000), E(1 ≤ E ≤ 100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B가 주어진다. 이는 A번 정점과 B번 정점이 연결되어 있다는 의미이다. 이때 방향은 A → B가 된다.
정점은 1부터 V까지 번호가 매겨져 있다.
▸ 출력
첫째 줄에 SCC의 개수 K를 출력한다. 다음 K개의 줄에는 각 줄에 하나의 SCC에 속한 정점의 번호를 출력한다. 각 줄의 끝에는 -1을 출력하여 그 줄의 끝을 나타낸다. 각각의 SCC를 출력할 때 그 안에 속한 정점들은 오름차순으로 출력한다. 또한 여러 개의 SCC에 대해서는 그 안에 속해있는 가장 작은 정점의 정점 번호 순으로 출력한다.
문제 풀이
무향(양방향) 그래프에는 오일러 회로를 찾을 수 있는 이중 결합 컴포넌트의 개념이 있다면. 방향 그래프에는 강결합 컴포넌트(SCC)의 개념이 있다. 그래프 상 두 정점 u, v에 대해 양 방향으로 가는 경로가 모두 있을 때 두 정점은 같은 SCC에 속해있다고 말한다.

강결합 컴포넌트를 분리를 위해 타잔(Tarjan) 알고리즘을 사용할 것이다.
DFS가 어떤 SCC를 처음 방문했다고 하자. 이 정점을 x라 한다. 한 SCC에 속한 두 정점 간에는 항상 경로가 있기 때문에, DFS은 dfs(x)를 종료하기 전에 같은 SCC에 속한 정점을 전부 방문하게 된다. 따라서 이 SCC에 속한 정점들은 모두 x를 루트로 하는 서브트리에 포함된다.
간선 자를지에 대한 여부
역방향 간선 찾기
트리 간선 (u,v)를 자른다는 것은 v에서 u로 갈 수 있는 경로가 없다는 뜻이다. v에서 u로 가는 경로에는 항상 역방향 간선이 하나 이상 포함되어 있어야 하므로, 이 점을 응용하자.
- v를 루트로 하는 서브트리를 탐색하면서 만나는 역방향 간선을 이용해 닿을 수 있는 가장 높은 정점을 찾는다.
- 이 정점이 u 혹은 그보다 높이 있는 정점이라면 이 역방향 간선을 통해 v에서 u로 갈 수 있으므로 해당 간선은 자르면 안된다.

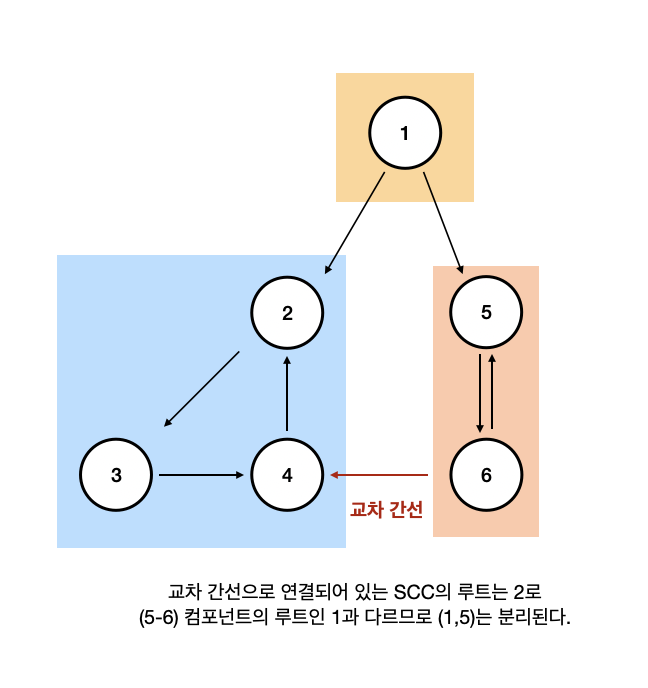
교차 간선
추가로 교차 간선도 고려해줘야 한다. v를 루트로 하는 서브트리에서 밖으로 나가는 역방향 간선이 하나도 없더라도 교차간선이 다른 정점을 통해 부모로 갈 수 있다면 (u,v)를 자를 수 없게 된다. 하지만 모든 교차 간선을 통해 루트로 올라갈 수 있는 것은 아니다. 교차간선을 어떻게 구분할까?
교차 간선으로 이어져 있는 정점이 SCC인지 아닌지에 대해 판단하면 된다.
- 만약 연결되어 있는 정점은 SCC로 묶여있다면 해당 컴포넌트의 루트를 구해준다.
- 만약 현재 탐색하는 구간의 루트와 일치한다면 같은 SCC로 묶이게 될 것이고 아니라면 SCC는 3개로 나뉘게 된다.
타잔 알고리즘 구현
- discovered[cur] = idx++; 정점의 도착 순서를 저장한다.
- stack.push(cur); cur의 서브트리들은 차례대로 stack에 저장된다.
- cur의 간선을 통해 인접 정점을 탐색한다.
- if(discovered[nxt]==-1) 방문하지 않은 노드라면 재귀를 통해 계속 탐색한다.
- ret = Math.min(ret, scc(nxt));
- else if(sccId[nxt]==-1) 이미 방문한 노드라면 해당 컴포넌트의 루트와 현재 cur노드의 루트와 비교한다.
- ret = Math.min(ret, discovered[nxt]);
- if(discovered[nxt]==-1) 방문하지 않은 노드라면 재귀를 통해 계속 탐색한다.
- if(ret == discovered[cur]) scc 컴포넌트의 루트가 반환되면 해당 서브트리에 속한 정점들은 하나의 컴포넌트로 묶는다.
static int scc(int cur) {
discovered[cur] = idx++;
stack.push(cur);
int ret = discovered[cur];
for(int i=0; i<list[cur].size(); i++) {
int nxt = list[cur].get(i);
if(discovered[nxt]==-1) { //방문하지 않은 노드
ret = Math.min(ret, scc(nxt));
} else if(sccId[nxt]==-1) { // 이미 방문한 노드라면 해당 컴포넌트의 루트와 현재 cur노드의 루트와 비교한다.
ret = Math.min(ret, discovered[nxt]);
}
}
// 역방향 간선이 부모(cur) 이하이면 scc로 묶는다.
if(ret == discovered[cur]) {
Queue<Integer> q = new PriorityQueue<>();
while(true) {
int t = stack.pop();
q.add(t);
sccId[t] = sccCnt;
if(t == cur) break;
}
result.add(q);
sccCnt++;
}
return ret;
}
풀이 코드
import java.io.*;
import java.util.*;
public class Main {
static int idx, sccCnt=0;
static int[] discovered, sccId;
static List<Integer>[] list;
static Stack<Integer> stack;
static List<Queue<Integer>> result;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int v = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
list = new ArrayList[v+1];
discovered = new int[v+1]; // 각 정점 발견 순서
sccId = new int[v+1]; // 각 정점 컴포넌트 번호
for(int i=1; i<v+1; i++) {
list[i] = new ArrayList<>();
discovered[i] = -1;
sccId[i] = -1;
}
for(int i=0; i<e; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
list[a].add(b);
}
result = new ArrayList<>();
stack = new Stack<>();
for(int i=1; i<v+1; i++) {
if(discovered[i] == -1) {
scc(i);
}
}
System.out.println(sccCnt);
Collections.sort(result, (o1,o2) -> o1.peek()-o2.peek());
StringBuilder sb = new StringBuilder();
for(Queue<Integer> q : result ) {
while(!q.isEmpty()) {
sb.append(q.poll()+" ");
}
sb.append(-1+"\n");
}
System.out.println(sb.toString());
}
static int scc(int cur) {
discovered[cur] = idx++;
stack.push(cur);
int ret = discovered[cur];
for(int i=0; i<list[cur].size(); i++) {
int nxt = list[cur].get(i);
if(discovered[nxt]==-1) { //방문하지 않은 노드
ret = Math.min(ret, scc(nxt));
} else if(sccId[nxt]==-1) { // 방문했지만 scc에 속하지 않은 노드
ret = Math.min(ret, discovered[nxt]);
}
}
// 역방향 간선이 부모(cur) 이하이면 scc로 묶는다.
if(ret == discovered[cur]) {
Queue<Integer> q = new PriorityQueue<>();
while(true) {
int t = stack.pop();
q.add(t);
sccId[t] = sccCnt;
if(t == cur) break;
}
result.add(q);
sccCnt++;
}
return ret;
}
}'Dot Algo∙ DS > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘] 이분 매칭 (Bipartite Matching) 알고리즘 (Java) (0) | 2022.01.01 |
|---|---|
| [알고리즘] 네트워크 유량, 포드-폴커슨(Ford-Fulkerson) 알고리즘 (Java) (0) | 2021.12.27 |
| [알고리즘] 단절점 (백준 11266번 풀이) (0) | 2021.12.03 |
| [알고리즘] 다중 문자열 검색 아호 코라식(Aho-Corasick) 알고리즘 정리 (Java) (0) | 2021.11.29 |
| [알고리즘] 최적화 문제 결정 문제로 바꿔풀기 - 파라메트릭 서치(Parametric Search) (0) | 2021.10.22 |




