#1199 오일러 회로
난이도 : 플레 5
유형 : 그래프 탐색 / DFS / 오일러 회로
1199번: 오일러 회로
첫 줄에는 정점의 수 N(1 ≤ N ≤ 1,000)이 주어진다. 그리고 다음 N개의 줄에 대해 인접행렬의 정보가 주어진다. i+1번째 줄에는 i번 정점에 대한 인접행렬이 주어진다. 두 정점 사이에 간선이 여러
www.acmicpc.net
▸ 문제
어느 점에서 출발하여 그래프 상에 있는 모든 간선을 지나되 한번 지난 간선은 다시 지나지 않고 출발점으로 돌아오는 회로를 오일러 회로라 한다. 단, 그래프는 양방향 그래프가 주어진다.
문제는 그래프가 주어졌을 때 오일러 회로 경로를 출력하는 것이다.
▸ 입력
첫 줄에는 정점의 수 N(1 ≤ N ≤ 1,000)이 주어진다. 그리고 다음 N개의 줄에 대해 인접행렬의 정보가 주어진다. i+1번째 줄에는 i번 정점에 대한 인접행렬이 주어진다. 두 정점 사이에 간선이 여러 개 있을 수 있다. 인접행렬의 값은 두 정점 사이의 간선 개수를 의미하며, 0보다 크거나 같고, 10보다 작거나 같은 정수이다.
입력으로 주어지는 그래프에는 루프 (양 끝점이 같은 간선)는 없다. 또, 입력으로 주어지는 그래프는 모두 연결되어 있다.
▸ 출력
첫 줄에 방문하는 점 순서를 공백으로 구분하여 출력한다. 단, 시작점은 어느 위치에서든 상관없고 아무 경로만 하나 찍으면 된다. 불가능한 경우에는 -1을 출력한다.
문제 풀이
오일러회로 성립 조건
그래프에서 최대한 많은 간선의 경로를 그렸을 때 시작점을 u, 끝점을 v라 하자.
u != v인 경우
항상 v는 홀수 개의 간선과 인접해 있을 것이다. v를 지나가기 위해서는 v 진입 차수 1개, 진출 차수 1개가 필요한 데 진입해서 진출할 수 없다는 뜻은 인접한 간선의 수가 홀수라는 의미이기 때문이다.
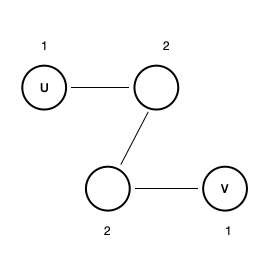
u = v인 경우
v에 인접한 간선의 수는 항상 짝수이다. u에서 나가는 것으로 시작했으니, 들어온 뒤 다시 나갈 수 없다면 지금까지 사용한 간선의 수는 항상 짝수여야 하기 때문이다.
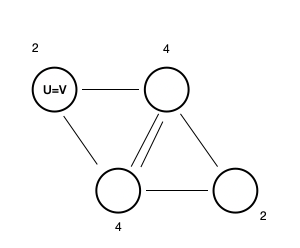
모든 간선을 지나면서 출발점과 도착점이 같은 오일러 회로는 각 정점에 인전한 간선의 수와 밀접한 연관이 있다. 오일러 회로는 모든 정점에 들어가는 횟수와 나오는 횟수(진출 차수 == 진입 차수)가 같아야 하는데, 홀수점이라면 이와 같은 일이 불가능해진다.
따라서 그래프의 모든 정점들이 짝수점이어야만 오일러 회로가 존재할 수 있다.
설계
- 각 정점의 간선 정보를 인접 배열 데이터에 저장한다.
- 한 정점의 차수 짝수가 아니라면 -1 을 출력하고 종료한다.
- DFS 탐색을 통해 오일러 회로를 찾는다. getEulerCircuit(0);
- 연결되어 있는 간선이 있으면 양쪽 간선을 모두 제거해준다.
- arr[cur][nxt]--;
- arr[nxt][cur]--;
- 그리고 다음 정점을 탐색한다. getEulerCircuit(nxt);
- 경로는 재귀 함수가 반환되는 순대로 cur을 입력받아서 출력한다. sb.append((cur+1)+" ");
- 연결되어 있는 간선이 있으면 양쪽 간선을 모두 제거해준다.
풀이 코드
import java.io.*;
import java.util.*;
public class Main {
static int n;
static int[][] arr;
static StringBuilder sb;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
arr = new int[n][n];
StringTokenizer st;
for(int i=0; i<n; i++) {
int vertex = 0;
st = new StringTokenizer(br.readLine());
for(int j=0; j<n; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
vertex += arr[i][j];
}
if(vertex%2!=0) {
System.out.println(-1);
return;
}
}
sb = new StringBuilder();
getEulerCircuit(0);
System.out.println(sb.toString());
}
static void getEulerCircuit(int cur) {
for(int nxt=0; nxt<arr.length; nxt++) {
while(arr[cur][nxt] > 0) {
arr[cur][nxt]--;
arr[nxt][cur]--;
getEulerCircuit(nxt);
}
}
sb.append((cur+1)+" ");
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 14442번 벽 부수고 이동하기 2 (Java) (0) | 2021.12.07 |
|---|---|
| [BOJ] 백준 5719번 거의 최단 경로 (Java) (0) | 2021.12.06 |
| [BOJ] 백준 10216번 Count Circle Group (Java) (0) | 2021.12.02 |
| [BOJ] 백준 10256번 돌연변이 (Java) (0) | 2021.12.01 |
| [BOJ] 백준 3197번 백조의 호수 (Java) (0) | 2021.11.30 |




