#5719 거의 최단 경로
난이도 : 플레 5
유형 : 그래프 탐색 / 다익스트라
5719번: 거의 최단 경로
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 장소의 수 N (2 ≤ N ≤ 500)과 도로의 수 M (1 ≤ M ≤ 104)가 주어진다. 장소는 0부터 N-1번까지 번호가 매겨져 있
www.acmicpc.net
▸ 문제
요즘 많은 자동차에서는 GPS 네비게이션 장비가 설치되어 있다. 네비게이션은 사용자가 입력한 출발점과 도착점 사이의 최단 경로를 검색해 준다. 하지만, 교통 상황을 고려하지 않고 최단 경로를 검색하는 경우에는 극심한 교통 정체를 경험할 수 있다.
상근이는 오직 자기 자신만 사용 가능한 네비게이션을 만들고 있다. 이 네비게이션은 절대로 최단 경로를 찾아주지 않는다. 항상 거의 최단 경로를 찾아준다.
거의 최단 경로란 최단 경로에 포함되지 않는 도로로만 이루어진 경로 중 가장 짧은 것을 말한다.
예를 들어, 도로 지도가 아래와 같을 때를 생각해보자. 원은 장소를 의미하고, 선은 단방향 도로를 나타낸다. 시작점은 S, 도착점은 D로 표시되어 있다. 굵은 선은 최단 경로를 나타낸다. (아래 그림에 최단 경로는 두 개가 있다)거의 최단 경로는 점선으로 표시된 경로이다. 이 경로는 최단 경로에 포함되지 않은 도로로 이루어진 경로 중 가장 짧은 경로이다. 거의 최단 경로는 여러 개 존재할 수도 있다. 예를 들어, 아래 그림의 길이가 3인 도로의 길이가 1이라면, 거의 최단 경로는 두 개가 된다. 또, 거의 최단 경로가 없는 경우도 있다.

▸ 입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 장소의 수 N (2 ≤ N ≤ 500)과 도로의 수 M (1 ≤ M ≤ 104)가 주어진다. 장소는 0부터 N-1번까지 번호가 매겨져 있다. 둘째 줄에는 시작점 S와 도착점 D가 주어진다. (S ≠ D; 0 ≤ S, D < N) 다음 M개 줄에는 도로의 정보 U, V, P가 주어진다. (U ≠ V ; 0 ≤ U, V < N; 1 ≤ P ≤ 103) 이 뜻은 U에서 V로 가는 도로의 길이가 P라는 뜻이다. U에서 V로 가는 도로는 최대 한 개이다. 또, U에서 V로 가는 도로와 V에서 U로 가는 도로는 다른 도로이다.
입력의 마지막 줄에는 0이 두 개 주어진다.
▸ 출력
각 테스트 케이스에 대해서, 거의 최단 경로의 길이를 출력한다. 만약, 거의 최단 경로가 없는 경우에는 -1을 출력한다.
문제 풀이
아이디어는 쉬운데 구현이 좀 까다로운 다익스트라 심화 문제이다. 첫 번째 최단경로가 아닌 두 번째 최단경로를 구해주면 된다. 해당 구현에서 가장 중요한 부분은 첫 번째 최단경로를 tracking하는 것이다.
다익스트라 최단 경로 tracking하기
기본 다익스트라 코드는 다음과 같다. 우선순위 큐와 DP로 최단 경로를 찾는 단순한 그래프 알고리즘이다.
// 기본 다익스트라
static void dijkstra(int s) {
Queue<Node> q = new PriorityQueue<>();
initDp();
dp[s] = 0;
q.add(new Node(s,0));
while(!q.isEmpty()) {
Node node = q.poll();
int cur = node.to;
if(node.w > dp[cur]) continue;
for(Node nxt : list[cur]) {
if(dp[nxt.to] >= dp[cur] + nxt.w) {
dp[nxt.to] = dp[cur] + nxt.w;
q.add(new Node(nxt.to, dp[nxt.to]));
}
}
}
}
여기서 최단 경로를 모두 추적해주기 위해서는 인접리스트 배열을 하나 더 사용하여 저장해주면 된다.
- if(dp[nxt.to] > dp[cur] + nxt.w)
- 최단 경로가 갱신되면 해당 경로에 저장된 인접리스트 배열을 초기화해주고 새로 저장해준다.
- else if(dp[nxt.to] == dp[cur] + nxt.w)
- 기존과 최단 경로 길이가 같다면 같이 저장해준다.
시뮬레이션을 돌리면 다음과 같다.
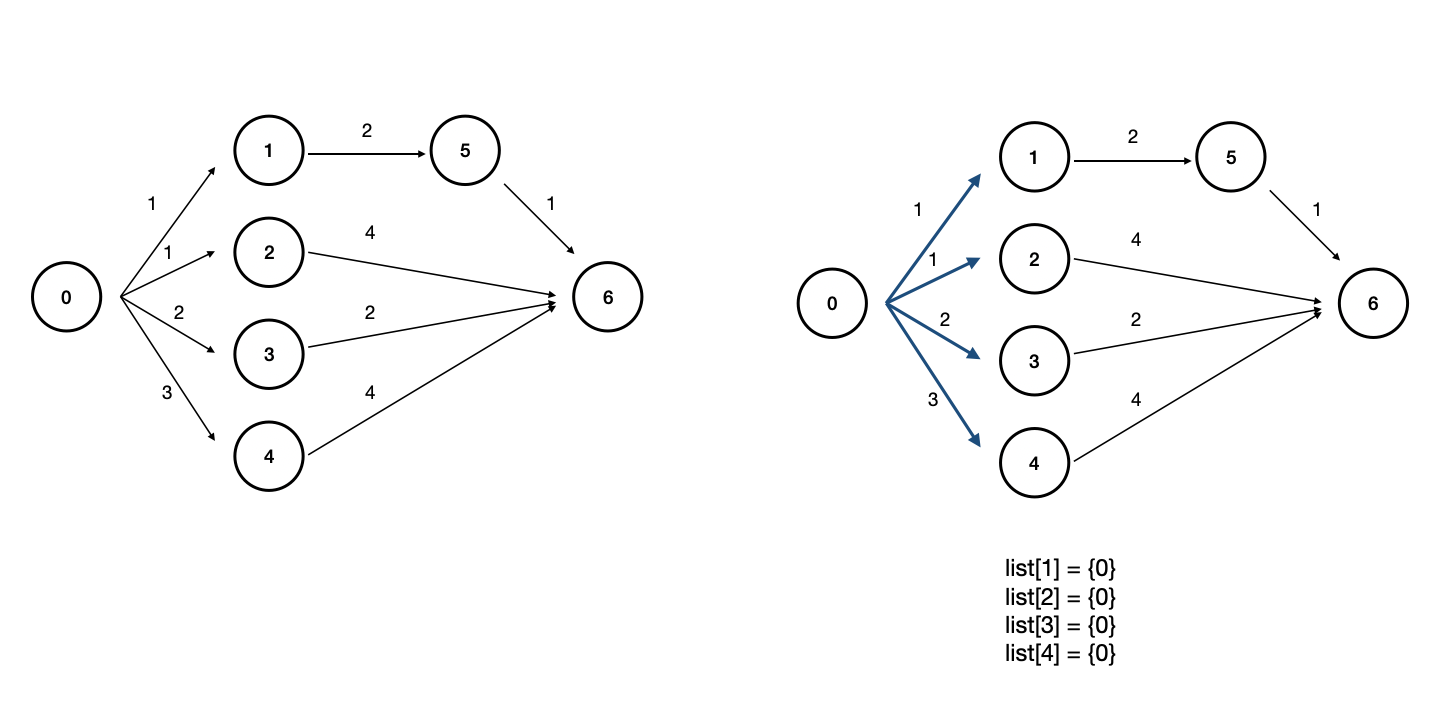
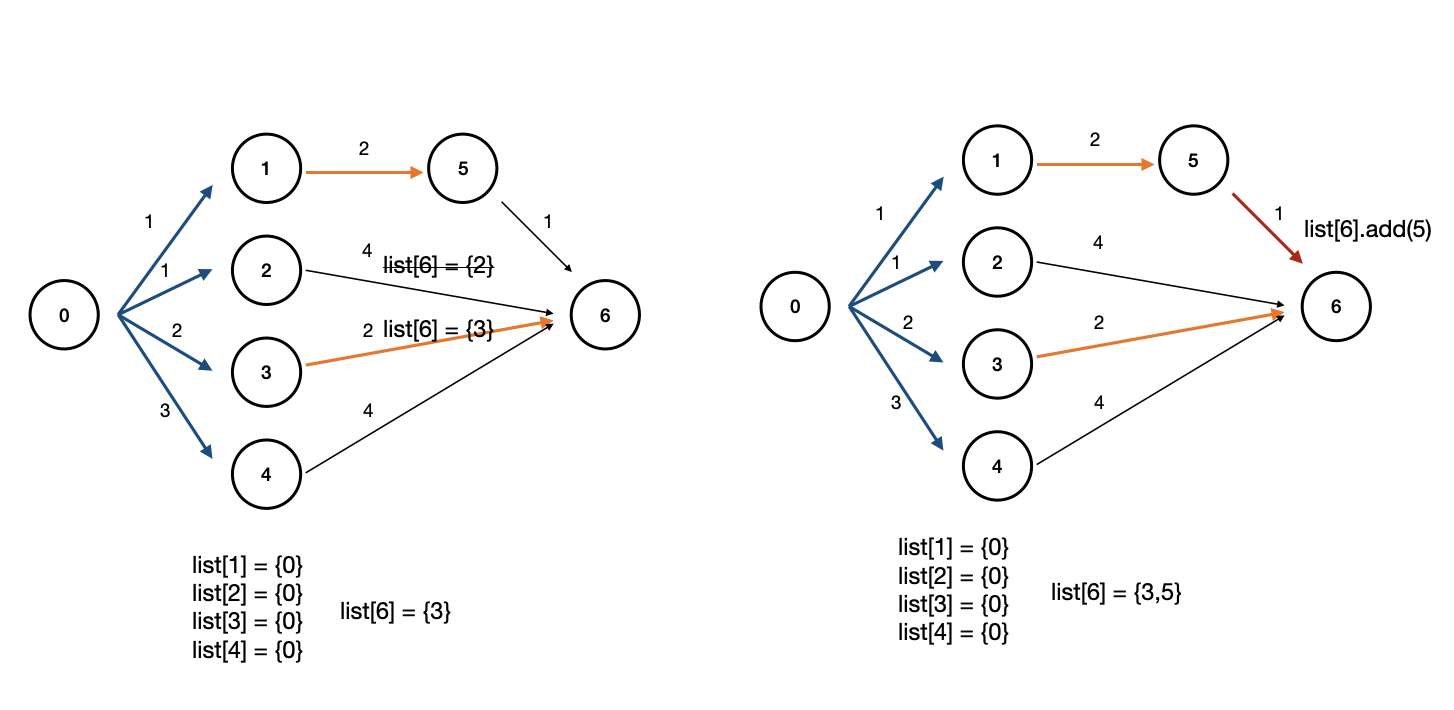
간선 weight가 낮은 1,2번부터 탐색하게 된다. 2번은 바로 6번과 연결되기 때문에 6번 노드에 대한 추적 데이터가 초기화되어 저장되지만 후에 도착하는 3번 노드에 의해 재초기화된다. 최단거리 값이 갱신되었기 때문이다. 그리고 마지막으로 도착하는 5번 노드의 경로 또한 최단거리 값과 동일하기 때문에 같이 저장된다.
그러면 다음과 같이 다익스트라를 구현해볼 수 있다.
static void dijkstra(int s, int d) {
Queue<Node> q = new PriorityQueue<>();
initDp();
dp[s] = 0;
q.add(new Node(s,0));
while(!q.isEmpty()) {
Node node = q.poll();
int cur = node.to;
if(node.w > dp[cur]) continue;
for(Node nxt : list[cur]) {
if(exRoute[cur][nxt.to]) continue;
if(dp[nxt.to] > dp[cur] + nxt.w) {
dp[nxt.to] = dp[cur] + nxt.w;
removeList[nxt.to] = new ArrayList<>();
removeList[nxt.to].add(cur);
q.add(new Node(nxt.to, dp[nxt.to]));
}else if(dp[nxt.to] == dp[cur] + nxt.w) {
removeList[nxt.to].add(cur);
}
}
}
}
설계
- 입력 정보를 인접리스트 배열에 저장한다.
- list[u].add(new Node(v,cost));
- 첫 번째 최단 경로를 다익스트라를 통해 구한다. dijkstra(s);
- 첫 번째 최단 경로에 해당하는 간선을 추적하여 저장한다. removeList[nxt.to].add(cur);
- 추척한 경로를 boolean배열을 통해 탐색 불가하게 설정해준다. exRoute[nxt][d] = true;
- 그리고 다익스트라 알고리즘을 통해 최단 경로를 재탐색을 해준다. dijkstra(s);
- 경로가 없다면 -1 최단 경로가 있다면 해당 최단 거리를 출력한다.
풀이 코드
import java.io.*;
import java.util.*;
public class Main {
static class Node implements Comparable<Node>{
int to;
int w;
public Node(int to, int w) {
this.to = to;
this.w = w;
}
public int compareTo(Node o) {
return this.w - o.w;
}
}
static final int MAX = Integer.MAX_VALUE;
static int n,m;
static int[] dp;
static boolean[][] exRoute;
static List<Node>[] list;
static List<Integer>[] removeList;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
String input = null;
StringBuilder sb = new StringBuilder();
while(!(input=br.readLine()).equals("0 0")) {
st = new StringTokenizer(input);
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int d = Integer.parseInt(st.nextToken());
list = new ArrayList[n];
removeList = new ArrayList[n];
dp = new int[n];
for(int i=0; i<n; i++) {
list[i] = new ArrayList<>();
removeList[i] = new ArrayList<>();
}
for(int i=0; i<m; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
list[u].add(new Node(v,cost));
}
exRoute = new boolean[n][n];
dijkstra(s);
removeMinRouteVertex(s,d);
dijkstra(s);
sb.append(dp[d]== MAX? -1 : dp[d]);
sb.append("\n");
}
System.out.println(sb.toString());
}
static void initDp() {
Arrays.fill(dp, MAX);
}
static void removeMinRouteVertex(int s, int d) {
if(s==d) return;
for(int nxt : removeList[d]) {
if(!exRoute[nxt][d]) {
exRoute[nxt][d] = true;
removeMinRouteVertex(s, nxt);
}
}
}
static void dijkstra(int s) {
Queue<Node> q = new PriorityQueue<>();
initDp();
dp[s] = 0;
q.add(new Node(s,0));
while(!q.isEmpty()) {
Node node = q.poll();
int cur = node.to;
if(node.w > dp[cur]) continue;
for(Node nxt : list[cur]) {
if(exRoute[cur][nxt.to]) continue;
if(dp[nxt.to] > dp[cur] + nxt.w) {
dp[nxt.to] = dp[cur] + nxt.w;
removeList[nxt.to] = new ArrayList<>();
removeList[nxt.to].add(cur);
q.add(new Node(nxt.to, dp[nxt.to]));
}else if(dp[nxt.to] == dp[cur] + nxt.w) {
removeList[nxt.to].add(cur);
}
}
}
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 19542번 전단지 돌리기 (Java) (0) | 2021.12.08 |
|---|---|
| [BOJ] 백준 14442번 벽 부수고 이동하기 2 (Java) (0) | 2021.12.07 |
| [BOJ] 백준 1199번 오일러 회로 (Java) (0) | 2021.12.04 |
| [BOJ] 백준 10216번 Count Circle Group (Java) (0) | 2021.12.02 |
| [BOJ] 백준 10256번 돌연변이 (Java) (0) | 2021.12.01 |




