#7812 중앙 트리
난이도 : 플레 5
유형 : 트리 / DFS
7812번: 중앙 트리
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫 줄에는 트리의 정점의 수 n이 주어진다. (1 ≤ n ≤ 10,000) 각 정점은 0번부터 n-1번까지 번호가 붙여져 있다. 다음 n-1개 줄
www.acmicpc.net
▸ 문제
트리는 사이클을 갖지 않는 연결된 그래프이다.
중앙 정점은 모든 정점으로 이르는 비용의 합이 가장 작은 정점이다. 트리의 정점 개수가 작은 경우에는 모든 경우의 수를 다 계산해보는 프로그램을 이용해 쉽게 구할 수 있다.
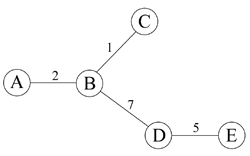
위의 그림은 가중치가 있는 트리로, 정점의 개수는 5개이다. 이 트리의 중앙 정점은 B이다.
B-A = 2, B-D = 7, B-C = 1, B-E = 7+5=12, 총: 2+1+7+12 = 22
N이 큰 경우에 문제를 풀어보자.
트리를 입력 받아, 모든 정점과 중앙 정점까지 비용의 합을 구하는 프로그램을 작성하시오.
▸ 입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫 줄에는 트리의 정점의 수 n이 주어진다. (1 ≤ n ≤ 10,000) 각 정점은 0번부터 n-1번까지 번호가 붙여져 있다. 다음 n-1개 줄에는 세 정수 a, b, w가 주어진다. (1 ≤ w ≤ 100) a와 b는 간선을 나타내고, w는 그 간선의 가중치이다.
입력의 마지막 줄에는 0이 하나 주어진다.
▸ 출력
각 테스트 케이스마다 모든 정점과 중앙 정점 사이의 비용의 합을 출력한다.
문제 풀이
dfs 활용이 필요한 트리 문제이다. 아이디어 내기가 쉽지않아서 crocus님의 풀이를 참고했다. 새로운 접근 방법이라 신선했다. 일단 모든 정점을 루트로 설정하고 최솟값을 구하면 최대 1만개의 정점을 가지는 트리 자료구조로는 무리가 있다. 그래서 하나의 트리 데이터만 구한 뒤 이를 이용해 다른 경우의 수를 모두 계산해야 한다.
계산하는 방법은 다음과 같다. 일단 각 루트일 경우 다른 정점과의 연관관계가 어떻게 설정되어있는지 확인해보자. 먼저 루트가 0일 때 트리의 데이터는 다음과 같이 구할 수 있다.
- size: 자신을 포함한 서브트리 정점의 갯수이다.
- cost: 서브트리로 부터 계산된 총 비용의 합이다.
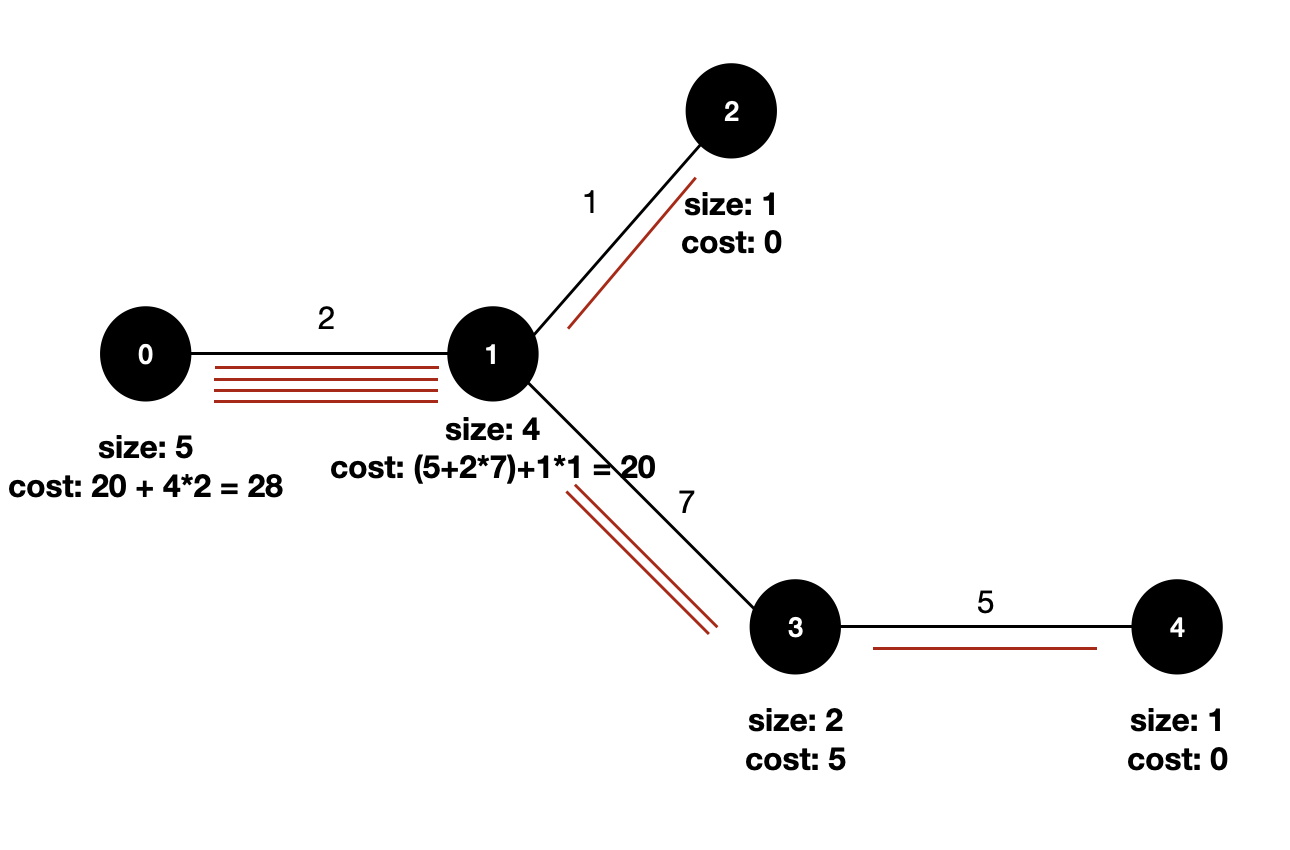
그럼 이제는 루트가 1일 때 트리의 데이터를 살펴보자.
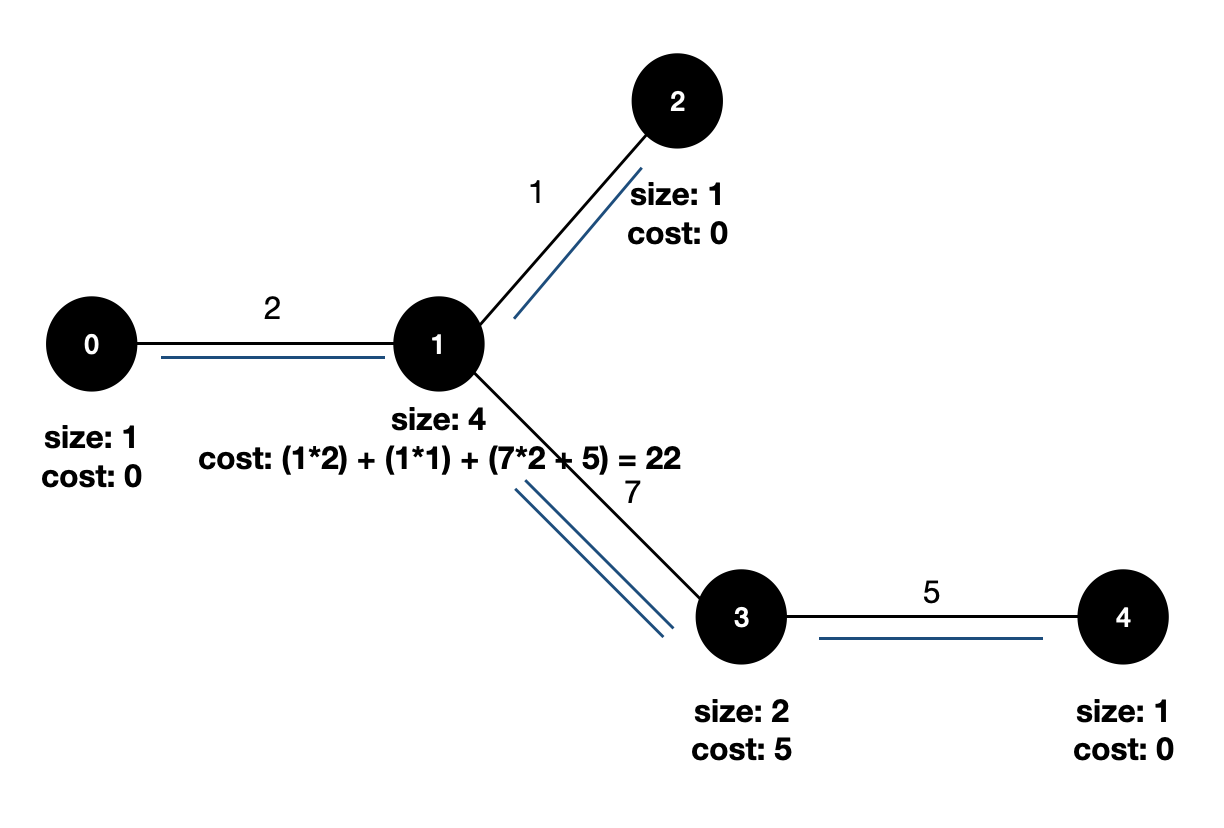
여기서 중요한 부분은 루트가 0 → 1로 이동할 때 발생하는 가변 데이터이다. 0-1을 잇는 size의 갯수가 달라진 것을 확인할 수 있다. 루트가 달라지니 해당 간선의 비중 또한 줄어들게 되는 것이다. 따라서 해당 부분의 가중치만 수정해주면 기존 데이터로 쉽게 다른 루트에 대한 데이터도 구할 수가 있게 되는 것이다.
- 현재 총합 - (기존 루트기준 가중치 * 간선 cost) + (이동한 루트기준 가중치 * 간선*cost)
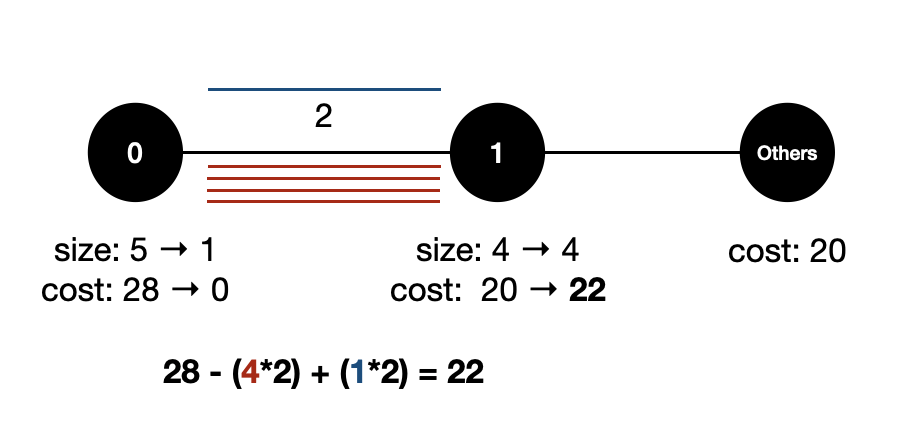
2번 예제도 똑같이 다뤄보면 다음과 같이 할 수 있다. 0번 루트에서 1번 루트로 이동한 경우이다.
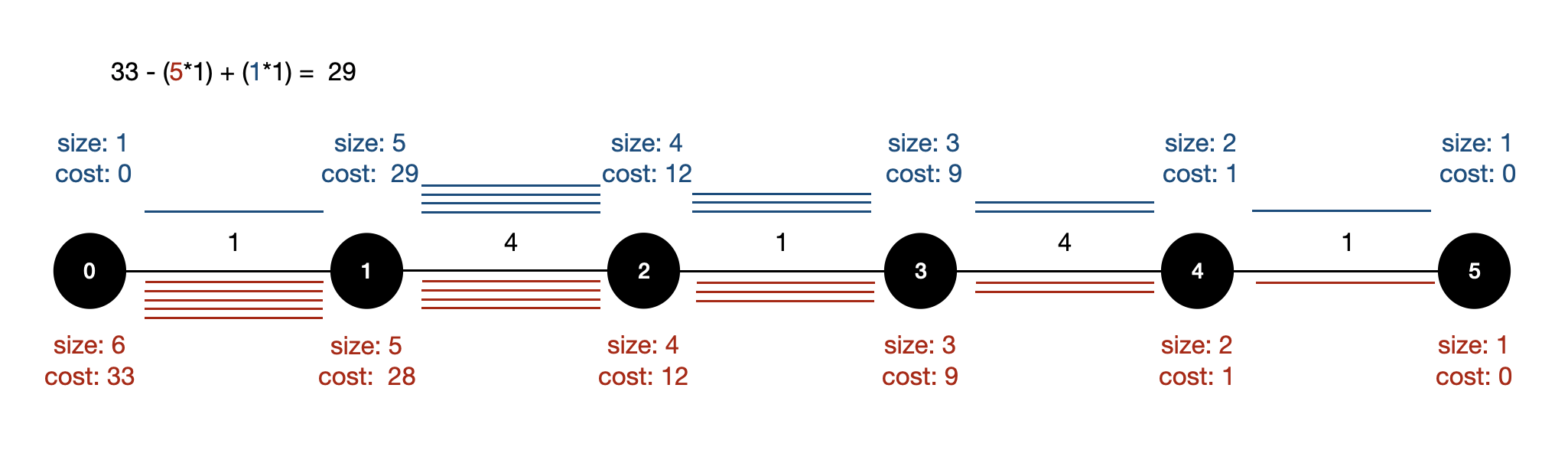
설계
- 양방향 트리 데이터를 입력받는다.
- 0번 루트를 기준으로 size와 누적된 cost의 값을 구한다. init(0,-1);
- 2번에서 구한 데이터를 기준으로 다른 노드를 탐색하며 각 루트에 대한 가중치를 구한 후 최솟값을 출력한다. getCostByRoot(0, -1, dp[0]);
- 현재 총합 - (기존 루트기준 가중치 * 간선 cost) + (이동한 루트기준 가중치 * 간선*cost)
풀이 코드
import java.io.*;
import java.util.*;
public class Main {
static int n;
static long res;
static int[] size;
static long[] dp;
static List<int[]>[] list;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
while(true) {
n = Integer.parseInt(br.readLine());
if(n==0) break;
dp = new long[n];
size = new int[n];
res = Long.MAX_VALUE;
list = new ArrayList[n];
for(int i=0; i<n; i++) {
list[i] = new ArrayList<>();
}
StringTokenizer st;
for(int i=0; i<n-1; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
list[a].add(new int[] {b,w});
list[b].add(new int[] {a,w});
}
init(0,-1);
getCostByRoot(0, -1, dp[0]);
sb.append(res+"\n");
}
System.out.println(sb.toString());
}
static void init(int cur, int pa) {
size[cur] = 1;
for(int[] nxt : list[cur]) {
if(nxt[0] != pa) {
init(nxt[0], cur);
size[cur] += size[nxt[0]];
dp[cur] += dp[nxt[0]] + nxt[1]*size[nxt[0]];
}
}
}
static void getCostByRoot(int cur, int pa, long cost) {
res = Math.min(res, cost);
for(int[] nxt : list[cur]) {
if(nxt[0] != pa) {
getCostByRoot(nxt[0], cur, cost- (size[nxt[0]]*nxt[1]) + (n-size[nxt[0]])*nxt[1]);
}
}
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 1806번 부분합 (Java) (0) | 2021.12.26 |
|---|---|
| [BOJ] 백준 14570번 나무 위의 구슬 (Java) (0) | 2021.12.25 |
| [BOJ] 백준 15480번 LCA와 쿼리 (Java) (0) | 2021.12.23 |
| [BOJ] 백준 8012번 한동이는 영업사원! (Java) (0) | 2021.12.22 |
| [BOJ] 백준 1865번 웜홀 (Java) (0) | 2021.12.21 |




