#2104 부분배열 고르기
난이도 : 플레 5
유형 : 세그먼트 트리 / 분할 정복
2104번: 부분배열 고르기
크기가 N(1 ≤ N ≤ 100,000)인 1차원 배열 A[1], …, A[N]이 있다. 어떤 i, j(1 ≤ i ≤ j ≤ N)에 대한 점수는, (A[i] + … + A[j]) × min{A[i], …, A[j]}가 된다. 즉, i부터 j까지의 합에 i부터 j까지의 최솟값을 곱
www.acmicpc.net
▸ 문제
크기가 N(1 ≤ N ≤ 100,000)인 1차원 배열 A[1], …, A[N]이 있다. 어떤 i, j(1 ≤ i ≤ j ≤ N)에 대한 점수는, (A[i] + … + A[j]) × min{A[i], …, A[j]}가 된다. 즉, i부터 j까지의 합에 i부터 j까지의 최솟값을 곱한 것이 점수가 된다.
배열이 주어졌을 때, 최대의 점수를 갖는 부분배열을 골라내는 프로그램을 작성하시오.
▸ 입력
첫째 줄에 정수 N이 주어진다. 다음 줄에는 A[1], …, A[N]을 나타내는 정수들이 주어진다. 각각의 정수들은 음이 아닌 값을 가지며, 1,000,000을 넘지 않는다.
▸ 출력
첫째 줄에 최대 점수를 출력한다.
문제 풀이
두 가지의 세그먼트 트리를 정의하여 풀이하여야 한다. 하나는 구간합을 구해주는 합 세그먼트 트리, 다른 하나는 최솟값을 알려주는 최소 인덱스 트리이다. 최솟값을 인덱스로 저장하는 이유는 구간을 분할 정복을 해야하는데 최솟값을 담는 인덱스 정보가 필요하기 때문이다.
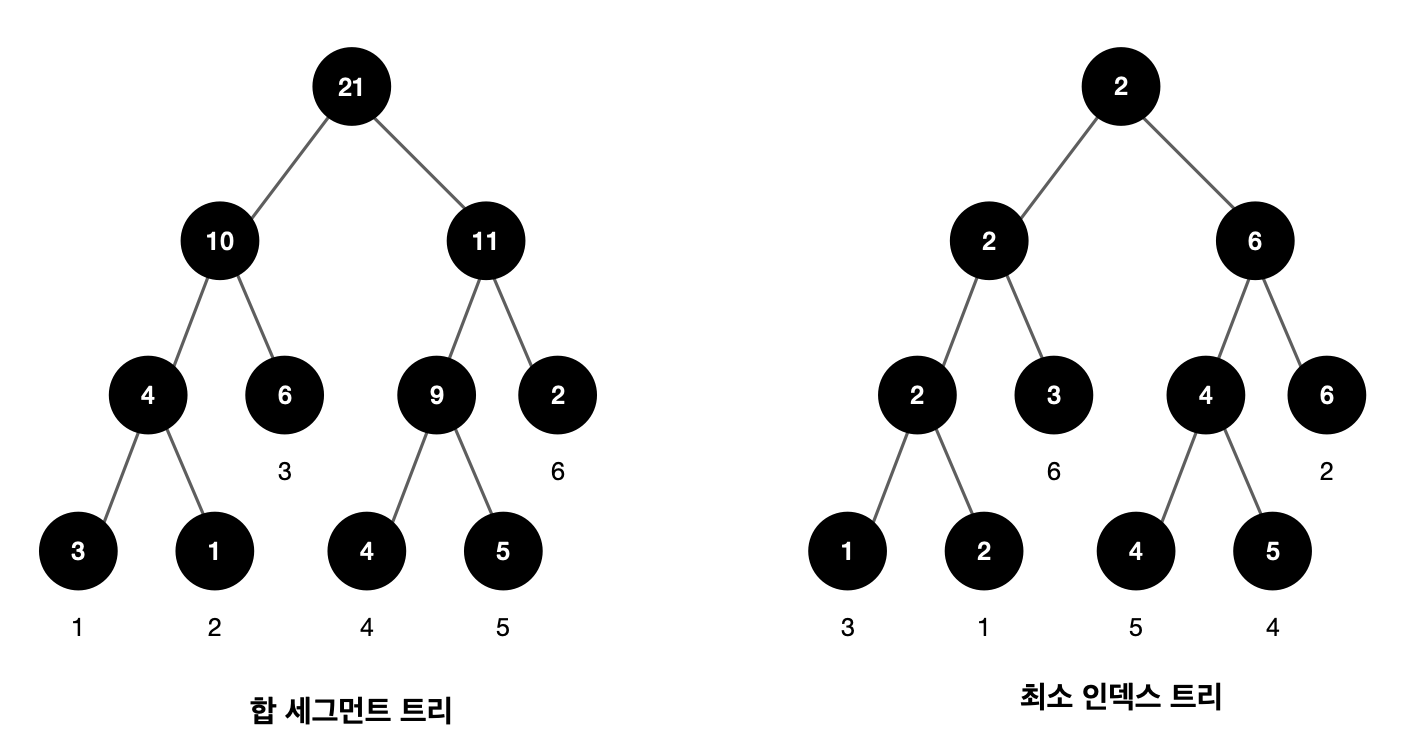
여기서 분할 정복을 사용하여 재귀로 최댓값을 가지는 부분 배열을 구해주면 된다.
- [s, e] 구간에서 가장 작은 최솟값(arr[minIdx] = min)을 구한다.
- long area = [s, e]의 구간합*최솟값(min)을 구한다.
- 최솟값 인덱스를 기준으로 왼쪽, 오른쪽 구간으로 나누어 재귀 탐색을 수행한다.
- [s ~ minIdx-1]
- [minIdx+1 ~ e]
- if(s==e)이라면 분할없이 그대로 area값을 반환한다.
풀이 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int n;
static int[] arr, minTree;
static long[] sumTree;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
arr = new int[n+1];
arr[0] = Integer.MAX_VALUE;
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=1; i<n+1; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
sumTree = new long[n*4];
minTree = new int[n*4];
sumInit(1, n, 1);
minInit(1, n, 1);
System.out.println(query(1,n));
}
static long query(int s, int e) {
int min = pMin(1, n, 1, s, e);
long area = pSum(1, n, 1, s, e)*arr[min];
if(s == e) return area;
if(s < min ) {
long tmp = query(s, min-1);
if(area < tmp) area = tmp;
}
if(min < e) {
long tmp = query(min+1, e);
if(area < tmp) area = tmp;
}
return area;
}
static long sumInit(int s, int e, int node) {
if(s == e) return sumTree[node] = arr[s];
int mid = (s+e)/2;
return sumTree[node] = sumInit(s, mid, node*2) + sumInit(mid+1, e, node*2+1);
}
static int minInit(int s, int e, int node) {
if(s == e) return minTree[node] = s;
int mid = (s+e)/2;
int left = minInit(s, mid, node*2);
int right = minInit(mid+1, e, node*2+1);
return minTree[node] = getIndex(left,right);
}
static long pSum(int s, int e, int node, int l, int r) {
if(e < l || r < s) return 0;
if(l <= s && e <= r) {
return sumTree[node];
}
int mid = (s+e)/2;
return pSum(s, mid, node*2, l, r) + pSum(mid+1, e, node*2+1, l, r);
}
static int pMin(int s, int e, int node, int l, int r) {
if(e < l || r < s) return 0;
if(l <= s && e <= r) {
return minTree[node];
}
int mid = (s+e)/2;
int left = pMin(s, mid, node*2, l, r);
int right = pMin(mid+1, e, node*2+1, l, r);
return getIndex(left,right);
}
static int getIndex(int left, int right) {
if(arr[left] < arr[right]) return left;
else return right;
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 7469번 K번째 수 (Java) (0) | 2022.01.18 |
|---|---|
| [BOJ] 백준 13537번 수열과 쿼리1 (Java) (0) | 2022.01.17 |
| [BOJ] 백준 14427번 수열과 쿼리 15 (Java) (0) | 2022.01.15 |
| [BOJ] 백준 12837번 가계부(Hard) (Java) - 펜웍 트리 (0) | 2022.01.14 |
| [BOJ] 백준 14428번 수열과 쿼리 16 (Java) (0) | 2022.01.13 |




