#13537 수열과 쿼리1
난이도 : 플레 3
유형 : 세그먼트 트리 / 머지소트 트리
13537번: 수열과 쿼리 1
길이가 N인 수열 A1, A2, ..., AN이 주어진다. 이때, 다음 쿼리를 수행하는 프로그램을 작성하시오. i j k: Ai, Ai+1, ..., Aj로 이루어진 부분 수열 중에서 k보다 큰 원소의 개수를 출력한다.
www.acmicpc.net
▸ 문제
길이가 N인 수열 A1, A2, ..., AN이 주어진다. 이때, 다음 쿼리를 수행하는 프로그램을 작성하시오.
- i j k: Ai, Ai+1, ..., Aj로 이루어진 부분 수열 중에서 k보다 큰 원소의 개수를 출력한다.
▸ 입력
첫째 줄에 수열의 크기 N (1 ≤ N ≤ 100,000)이 주어진다.
둘째 줄에는 A1, A2, ..., AN이 주어진다. (1 ≤ Ai ≤ 109)
셋째 줄에는 쿼리의 개수 M (1 ≤ M ≤ 100,000)이 주어진다.
넷째 줄부터 M개의 줄에는 쿼리 i, j, k가 한 줄에 하나씩 주어진다. (1 ≤ i ≤ j ≤ N, 1 ≤ k ≤ 109)
▸ 출력
각각의 쿼리마다 정답을 한 줄에 하나씩 출력한다.
문제 풀이
특정 구간의 k번째수, k보다 작은 수, 큰 수와 같은 문제는 머지소트 트리를 이용하여 풀이를 할 수 있다. 머지소트 트리는 세그먼트 트리의 형태를 지니고 있는 데 각 노드들이 리스트 구조를 있다는 점만 다르다.
예를 들어, [ 5 1 2 3 4 ]의 머지소트 트리를 만들면 다음과 같이 생성된다. 각 노드의 리스트들은 정렬을 시켜준 상태이다.
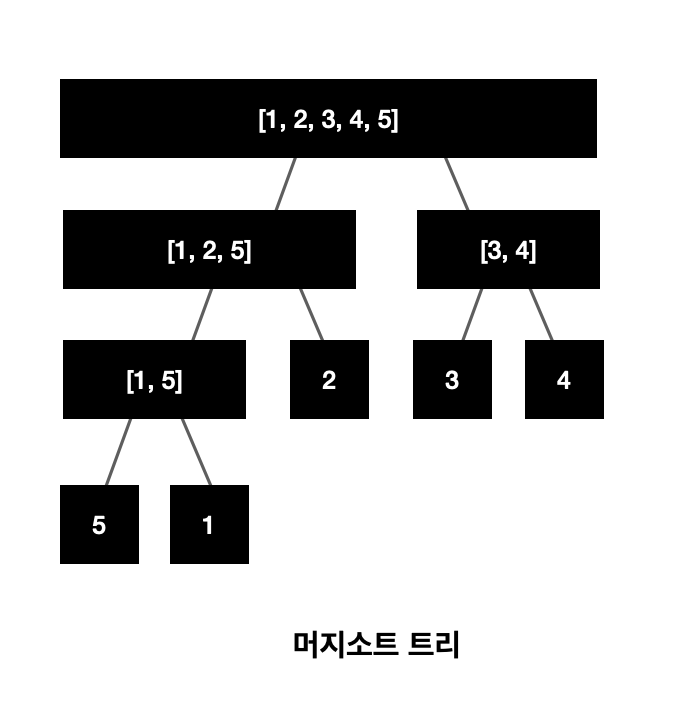
이제 여기서 각 구간에 들어가서 k보다 큰 원소의 개수(upperbound)를 구해주면 된다. 그렇게 구한 값을 리스트의 총 크기를 빼서 재귀로 쌓아준 다음 출력해주면 된다.
[2, 5] 구간에서 1보다 큰 원소의 개수 구하기
해당하는 구간에 가서 1보다 큰 원소의 개수를 각각 구해준다.
- 2번 구간에 해당하는 원소 1은 1과 같으므로 0개이다.
- 3번 구간에 해당하는 원소 2는 1보다 크므로 1개 존재한다.
- [4,5]번 구간에 해당하는 원소는 3, 4로 둘 다 1보다 크므로 2개 존재한다.
- 그래서 해당 쿼리는 총 3개를 출력해주면 된다
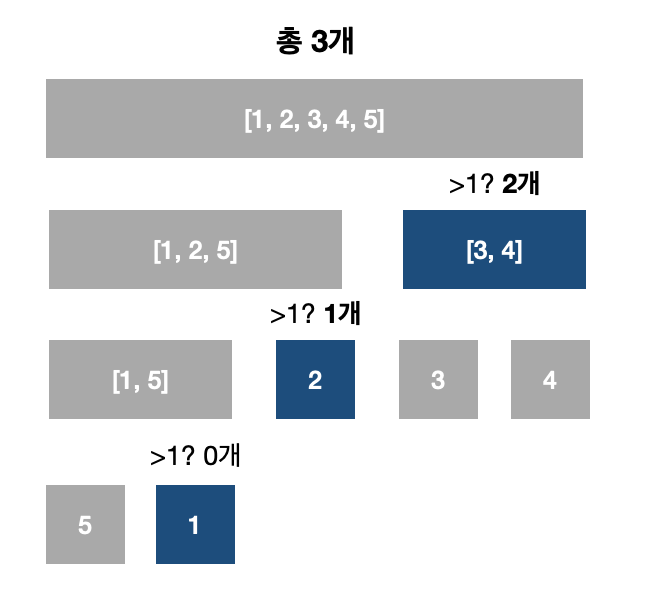
머지소트 트리를 생성하는 O(nlogn)이 걸리고, k보다 큰 수를 찾는 로직은 쿼리 로직안에 이분탐색도 존재하므로 O(m*log^2n)이 걸린다.
풀이 코드
import java.io.*;
import java.util.*;
public class Main {
static List<Integer>[] tree;
static int[] arr;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
arr = new int[n+1];
tree = new ArrayList[n*4];
for(int i=0; i<n*4; i++) {
tree[i] = new ArrayList<>();
}
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=1; i<=n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
update(1,n, 1, i);
}
for(int i=0; i<n*4; i++) {
Collections.sort(tree[i]);
}
StringBuilder sb = new StringBuilder();
int m = Integer.parseInt(br.readLine());
for(int i=0; i<m; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
sb.append(getMoreThanNumOfK(1,n,1,a,b,k) +"\n");
}
System.out.println(sb.toString());
}
static void update(int s, int e, int node, int idx) {
if(s > idx || e < idx ) return;
tree[node].add(arr[idx]);
if(s == e) return;
int mid = (s+e)/2;
update(s, mid, node*2, idx);
update(mid+1, e, node*2+1, idx);
}
static int getMoreThanNumOfK(int s, int e, int node, int l, int r, int k) {
if(r < s || l > e ) return 0;
if(l <= s && e <= r) {
int x = upperbound(tree[node], k); // [s,e]에서 k보다 큰 갯수
return tree[node].size()-x;
}
int mid = (s+e)/2;
return getMoreThanNumOfK(s, mid, node*2, l, r, k) + getMoreThanNumOfK(mid+1, e, node*2+1, l, r, k);
}
static int upperbound(List<Integer> data, int val) {
int s = 0;
int e = data.size();
while(s < e){
int mid = (s+e)/2;
if(data.get(mid) <= val) {
s = mid+1;
}else {
e = mid;
}
}
return e;
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 1450번 냅색문제 (Java) (0) | 2022.01.19 |
|---|---|
| [BOJ] 백준 7469번 K번째 수 (Java) (0) | 2022.01.18 |
| [BOJ] 백준 2104번 부분배열 고르기 (Java) (0) | 2022.01.16 |
| [BOJ] 백준 14427번 수열과 쿼리 15 (Java) (0) | 2022.01.15 |
| [BOJ] 백준 12837번 가계부(Hard) (Java) - 펜웍 트리 (0) | 2022.01.14 |




