#9426 중앙값 측정
난이도 : 플레 5
유형 : 세그먼트 트리 / 슬라이딩 윈도우
9426번: 중앙값 측정
첫째 줄에 N과 K가 주어진다. (1 ≤ N ≤ 250,000, 1 ≤ K ≤ 5,000, K ≤ N) 둘째 줄부터 N개 줄에 측정한 온도가 순서대로 주어진다. 온도는 0보다 크거나 같고, 65535보다 작거나 같은 정수이다.
www.acmicpc.net
▸ 문제
기상학에서 주요 사용하는 대표값은 중앙값이다. (중앙값의 정의는 힌트에 나와있다)
상근이는 1초에 한 번씩 온도를 재는 기계를 가지고 있고, 이 기계에 들어갈 소프트웨어를 작성하려고 한다. 기계에는 작은 디지털 디스플레이가 하나 달려있다. 매 초마다 디스플레이는 지난 K초동안 측정한 온도의 중앙값을 화면에 보여준다.
상근이는 소프트웨어를 기계에 올리기 전에 컴퓨터에서 테스트해보려고 한다.
총 N초 동안 측정한 온도가 주어졌을 때, 디스플레이에 표시된 중앙값의 합을 구하는 프로그램을 작성하시오. 즉, N개의 수가 주어졌을 때, 길이가 K인 연속 부분 수열 N-K+1개의 중앙값의 합을 구하는 프로그램을 작성하시오.
▸ 입력
첫째 줄에 N과 K가 주어진다. (1 ≤ N ≤ 250,000, 1 ≤ K ≤ 5,000, K ≤ N)
둘째 줄부터 N개 줄에 측정한 온도가 순서대로 주어진다. 온도는 0보다 크거나 같고, 65535보다 작거나 같은 정수이다.
▸ 출력
길이가 K인 모든 연속 부분 수열의 중앙값의 합을 출력한다.
문제 풀이
세그먼트 트리와 슬라이딩 윈도우 기법을 활용하여 풀이를 해야 한다. 중앙값은 길이가 K인 부분 수열에서 (K+1)/2번째 수를 나타낸다. 모든 값을 한번에 삽입하여 구간을 반복하기보다는 슬라이딩 윈도우를 사용하면 된다. 이전 값은 버리고 다음 값을 추가하면서 길이가 K인 수열을 유지하면서 가운데 값을 계속 뽑아주면 된다.
온도의 범위는 0부터 65535이기 때문에, 트리의 크기는 최대로 4*(65535+1)을 할당해주고 0부터 65535구간을 탐색해주면 된다. 왼쪽은 자신보다 작은 값, 오른쪽은 자신보다 큰 값의 개수를 나타내므로 다음과 같이 중앙값을 찾아주면 된다.
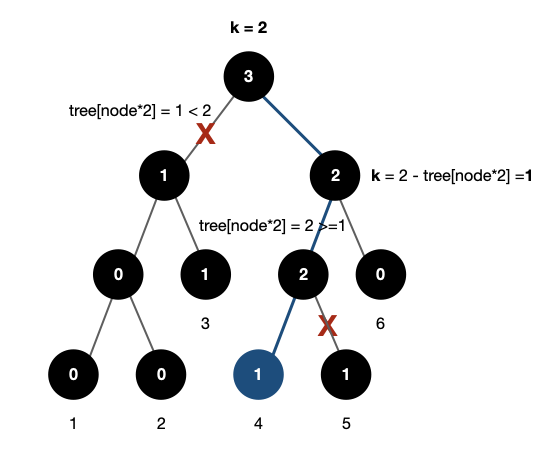
- tree[node*2] >= k, 왼쪽 자식 트리가 k보다 크므로 자신보다 작은 값이 나올 때까지 계속 재귀탐색한다.
- tree[node*2] < k, 왼쪽 자식 트리가 k보다 작으므로 자신보다 작은 개수를 빼주고 (k-tree[node*2]) 오른쪽 트리를 재귀 탐색한다.
만약 길이가 k=3인 [3, 4, 5]의 중앙값(k+1/2)을 구한다고 하면 다음과 같이 탐색한다.
풀이 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static final int SIZE = 65536;
static int[] arr, tree;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
arr = new int[n+1];
for(int i=1; i<=n; i++) {
arr[i] = Integer.parseInt(br.readLine());
}
tree = new int[SIZE*4];
for(int i=1; i<k; i++) {
update(0,SIZE,1,arr[i],1);
}
int prev = 1;
int mid = (k+1)/2;
long ans = 0;
for(int i=k; i<=n; i++) {
update(0,SIZE,1,arr[i],1);
ans += find(0,SIZE,1,mid);
update(0,SIZE,1,arr[prev++],-1);
}
System.out.println(ans);
}
static int update(int s, int e, int node, int idx, int dif) {
if(idx < s || e < idx) return tree[node];
if(s == e) {
return tree[node] += dif;
}
int mid = (s+e)/2;
return tree[node] = update(s, mid, node*2, idx, dif)+update(mid+1, e, node*2+1, idx, dif);
}
static int find(int s, int e, int node, int k) {
if(s == e) {
return s;
}
int mid = (s+e)/2;
if(tree[node*2] >= k) {
return find(s, mid, node*2, k);
}else {
return find(mid+1, e, node*2+1, k-tree[2*node]);
}
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 11658번 구간 합 구하기3 (Java) (0) | 2022.01.22 |
|---|---|
| [BOJ] 백준 13325번 이진 트리 (Java) (1) | 2022.01.21 |
| [BOJ] 백준 1450번 냅색문제 (Java) (0) | 2022.01.19 |
| [BOJ] 백준 7469번 K번째 수 (Java) (0) | 2022.01.18 |
| [BOJ] 백준 13537번 수열과 쿼리1 (Java) (0) | 2022.01.17 |




