#11658 구간 합 구하기3
난이도 : 플레 5
유형 : 펜윅 트리 / 누적합
11658번: 구간 합 구하기 3
첫째 줄에 표의 크기 N과 수행해야 하는 연산의 수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는
www.acmicpc.net
▸ 문제
N×N개의 수가 N×N 크기의 표에 채워져 있다. 그런데 중간에 수의 변경이 빈번히 일어나고 그 중간에 어떤 부분의 합을 구하려 한다. 표의 i행 j열은 (i, j)로 나타낸다.
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.
| 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 5 |
| 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 |
여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이 된다. (2, 3)을 7로 바꾸고 (2, 2)부터 (3, 4)까지 합을 구하면 3+7+5+4+5+6=30 이 된다.
표에 채워져 있는 수와 변경하는 연산과 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
▸ 입력
첫째 줄에 표의 크기 N과 수행해야 하는 연산의 수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 w, x, y, c 또는 다섯 개의 정수 w, x1, y1, x2, y2 가 주어진다. w = 0인 경우는 (x, y)를 c로 바꾸는 연산이고, w = 1인 경우는 (x1, y1)부터 (x2, y2)의 합을 구해 출력하는 연산이다. (1 ≤ c ≤ 1,000) 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다.
▸ 출력
w = 1인 입력마다 구한 합을 순서대로 한 줄에 하나씩 출력한다.
문제 풀이
2차원 배열의 구간 합을 구하는 문제로 누적합으로 풀어도 되고 펜윅 트리로 풀어도 된다.
- 누적합은 1열을 기준으로 누적합을 구하고 각 열별로 합을 구해서 더해주면 된다. 그래서 O(n*m)이 걸린다.
- 펜윅트리는 x열 탐색하는 데 logn, y열 탐색하는데 logn씩 소요된다. 그래서 O(m*(logn)^2)이 걸린다. 참고로 n > (logn)^2이다.
펜윅트리
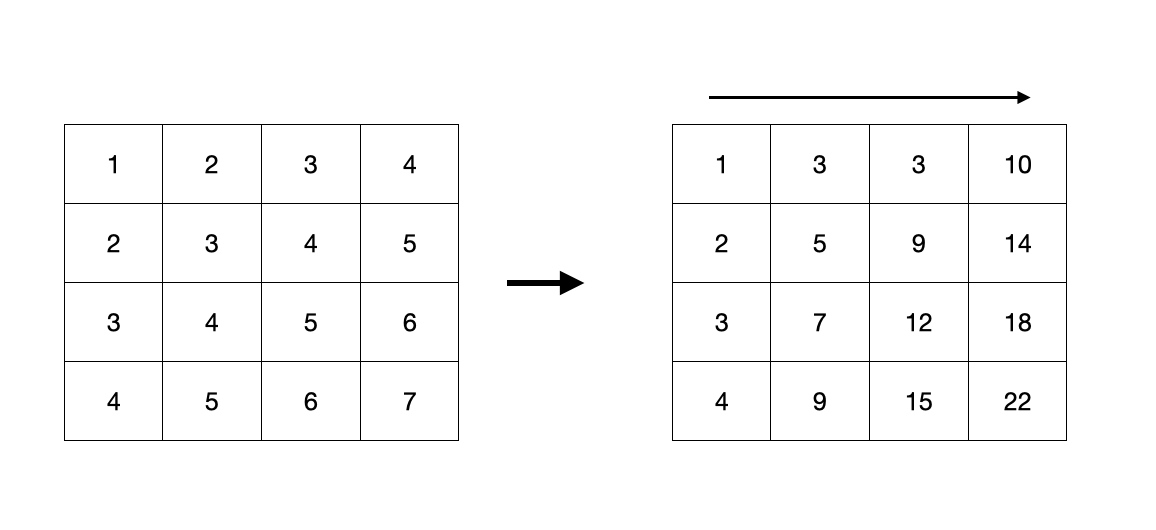
펜윅트리를 2차원 구조로 구해준다. 1차원적으로는 [1 2 3 4] → [1 3 3 10]와 같이 구해지는데, y축을 하나 더해줬다고 생각하면 된다.

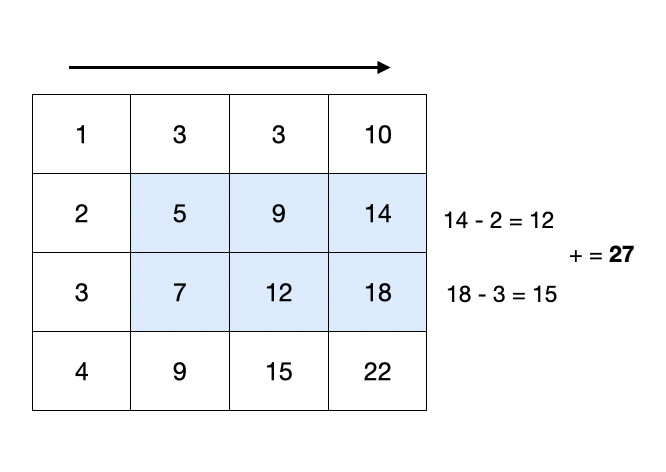
여기서 구간 합을 구해주는 방식은 1차원적으로는 sum(x2) - sum(x1-1)으로 더해주면 되는데, 2차원에서는 다음과 같이 중첩되는 부분은 빼주면서 구해주면 된다.

누적합
누적합 코드 또한 이와 똑같고 더 단순한 구조로 이루어져있다. 이는 2차원적이 아닌 단순 열 기준으로 누적합을 구해놓은 다음 각 열별로 구해주면 된다.
누적합의 구간합은 중복되는 부분이 없으니 뺄 부분은 없고 단순 각 열의 구간 합을 구해서 더해주면 된다.
펜윅트리 풀이 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int n;
static int[][] arr, tree;
static void update(int x, int y, int val) {
while(x <= n){
for(int i=y; i<=n;) {
tree[x][i] += val;
i += i&-i;
}
x += x&-x;
}
}
static int sum(int x, int y) {
int result = 0;
while(x > 0) {
for(int i=y; i>0;) {
result += tree[x][i];
i -= i&-i;
}
x -= x&-x;
}
return result;
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
arr = new int[n+1][n+1];
tree = new int[n+1][n+1];
for(int i=1; i<=n; i++) {
st = new StringTokenizer(br.readLine());
for(int j=1; j<=n; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
update(i,j,arr[i][j]);
}
}
StringBuilder sb = new StringBuilder();
for(int i=0; i<m; i++) {
st = new StringTokenizer(br.readLine());
int op = Integer.parseInt(st.nextToken());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
if(op == 1) {
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
sb.append((sum(x2, y2) - sum(x2, y1-1) - sum(x1-1, y2) + sum(x1-1,y1-1))+"\n");
}else {
int c = Integer.parseInt(st.nextToken());
update(x1, y1, c-arr[x1][y1]);
arr[x1][y1] = c;
}
}
System.out.println(sb.toString());
}
}
누적합 풀이 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int[][] arr, dp;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
arr = new int[n+1][n+1];
dp = new int[n+1][n+1];
for(int i=1; i<=n; i++) {
st = new StringTokenizer(br.readLine());
for(int j=1; j<=n; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
dp[i][j] = dp[i][j-1] + arr[i][j];
}
}
StringBuilder sb = new StringBuilder();
for(int i=0; i<m; i++) {
st = new StringTokenizer(br.readLine());
int op = Integer.parseInt(st.nextToken());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
if(op == 1) {
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
int res = 0;
for(int x=x1; x<=x2; x++) {
res += dp[x][y2] - dp[x][y1-1];
}
sb.append(res+"\n");
}else {
int c = Integer.parseInt(st.nextToken());
int dif = c - arr[x1][y1];
for(int y=y1; y<=n; y++) {
dp[x1][y] += dif;
}
arr[x1][y1] = c;
}
}
System.out.println(sb.toString());
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 18436번 수열과 쿼리 37 (Java) (0) | 2022.01.24 |
|---|---|
| [BOJ] 백준 12844번 XOR (Java) (0) | 2022.01.23 |
| [BOJ] 백준 13325번 이진 트리 (Java) (1) | 2022.01.21 |
| [BOJ] 백준 9426번 중앙값 측정 (Java) (0) | 2022.01.20 |
| [BOJ] 백준 1450번 냅색문제 (Java) (0) | 2022.01.19 |




