순열 (Permutation)

서로 다른 n개중 r개를 골라 순서를 고려해 나열한 경우의 수이다.
보통 가수들은 음반을 내면 트랙 번호가 1번부터 순서대로 매겨져 있다.
10곡이 있는데 이 중 5곡을 앨범에 넣고 트랙의 순서까지 정하려고 한다면 몇 가지의 경우의 수가 나올까?
앨범에 [ 1, 6, 9, 8, 5, 4 ]의 순서대로 실으려고 하다가 갑자기 마음이 바뀌어서 [ 6, 1, 9, 8, 5, 4, ] 1번과 2번 트랙의 순서를 바꿨고하자. 그러면 앨범에 속해있는 1, 4, 5, 6, 8 ,9의 곡은 같지만 순서가 다르기 때문에 다른 경우의 수로 세줘야 한다.
1) 10곡 중 1개 선택 : 10가지
2) 9곡 중 1개 선택 : 9가지
3) 8곡 중 1개 선택 : 8가지
4) 7곡 중 1개 선택 : 7가지
5) 6곡 중 1개 선택 : 6가지
→ 그래서 10개 중 5개를 순서를 상관하고 고르는 경우의 수는 총 10 * 9 * 8* 7 * 6 의 경우의 수가 나온다.
순열 코드
import java.util.*;
public class Main {
static int[] arr;
static boolean[] check;
static Stack<Integer> st;
public static void main(String[] args) {
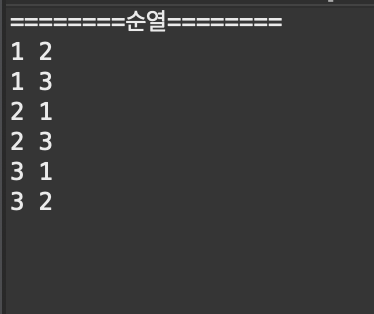
System.out.println("========순열========");
st = new Stack<>();
arr = new int[] {1,2,3};
check = new boolean[3];
permutation(3, 2);
}
//순열
static void permutation(int n, int r) {
if(st.size() == r){
for(int i : st){
System.out.print(i+" ");
}
System.out.println();
return;
}
for(int i=0; i<n; i++){
if(!check[i]){
check[i] = true;
st.push(arr[i]);
permutation(n, r);
st.pop();
check[i] = false;
}
}
}
}
조합 (Combination)
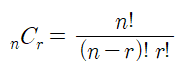
서로 다른 n개중에 r개를 선택하는 경우의 수이다. 순열과의 차이는 순서의 유무이다. 조합은 순서를 따지지 않는다.
10곡이 있는데 이 중 5곡을 앨범에 넣고 트랙의 순서를 고려하지 않는다면 몇 가지의 경우의 수가 나올까?
순서를 고려하지 않는다면 [ 1, 4, 5, 6, 8 ,9 ]을 앨범에 실을지만 정하면 되기 때문에 [ 1, 6, 9, 8, 5, 4 ]와 [ 6, 1, 9, 8, 5, 4, ]는 같은 경우의 수로 봐야한다.
1) 10곡 중 1개 선택 : 10가지
2) 9곡 중 1개 선택 : 9가지
3) 8곡 중 1개 선택 : 8가지
4) 7곡 중 1개 선택 : 7가지
5) 6곡 중 1개 선택 : 6가지
→ 순열은 여기서 끝이겠지만 조합은 총 10 * 9 * 8* 7 * 6 의 경우의 수 중에서 순서를 고려하지 않기 때문에 이미 정한 5곡의 순서를 메기는 경우의 수 5!를 나눠주면 된다. (곱의 법칙)
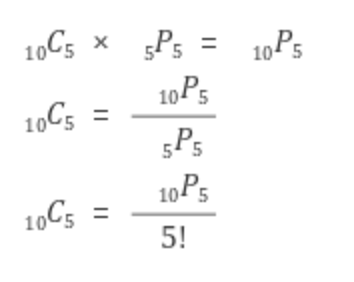
조합 코드
import java.util.*;
public class Main {
static int[] arr;
static boolean[] check;
static Stack<Integer> st;
public static void main(String[] args) {
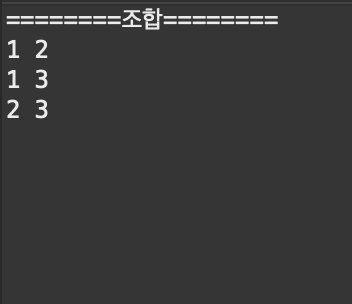
System.out.println("========조합========");
st = new Stack<>();
arr = new int[] {1,2,3};
check = new boolean[3];
combination(0, 2);
}
//조합
static void combination(int idx, int r) {
if(st.size()== r){
for(int i : st){
System.out.print(i+" ");
}
System.out.println();
return;
}
for(int i=idx; i<arr.length; i++) {
if(!check[i]) {
check[i] = true;
st.push(arr[i]);
combination(i, r);
st.pop();
check[i] = false;
}
}
}
}
중복 순열, 조합
중복 순열, 조합은 자기 자신을 중복으로 포함(ex. 11 , 22)하는 것이다.
만약 자신을 포함하여 카운트를 하고 싶다면 그냥 자신 방문 여부를 체크해주지 않으면 된다.
//순열 (자신 중복)
static void permutation2(int n, int r) {
if(st.size() == r){
for(int i : st){
System.out.print(i+" ");
}
System.out.println();
return;
}
for(int i=0; i<n; i++){
st.push(arr[i]);
permutation(n, r);
st.pop();
}
}
//조합 (자신 중복)
static void combination2(int idx, int r) {
if(st.size()==r) {
for(int i : st) {
System.out.print(i+" ");
}
System.out.println();
return;
}
for(int i=idx; i<arr.length; i++) {
st.push(arr[i]);
combination2(i, r);
st.pop();
}
}
나는 Stack과 재귀 함수를 활용하여 구했지만 boolean으로 방문 경로를 체크해줘서 탐색하든 재귀 매개변수 안에 데이터를 넣어 바로 출력하든 상황에 맞게 자기가 편한 방식과 성능을 고려하여 잘 사용하면 될 것 같다.
'Dot Algo∙ DS > 알고리즘 개념' 카테고리의 다른 글
| [자료구조] 세그먼트 트리 + Lazy Propagation (Java) (0) | 2021.07.08 |
|---|---|
| [알고리즘] 투 포인터와 슬라이딩 윈도우 (Java) (0) | 2021.07.07 |
| [알고리즘] 외판원 순회 문제(TSP: Travelling Salesman Problem) 정리 (Java) (0) | 2021.06.15 |
| [알고리즘] 소수(Prime Number) 구하기 - 에라토스테네스의 체 (Java) (0) | 2021.06.12 |
| [알고리즘] 비트(Bit)와 비트마스크(BitMask) 정리 (Java) (0) | 2021.05.31 |




