세그먼트 트리
기존에 세그먼트 트리를 이용한 문제는 구간 합을 구하는 쿼리와, 숫자 하나를 바꾸는 업데이트 쿼리로 이루어져 연속된 구간의 데이터의 합을 가장 빠르고 간단하게 구할 수 있는 트리이다.

하지만 하나의 숫자만 업데이트하는 것이 아니라 어떤 구간 [a,b]를 전부 업데이트하고 구간합을 구하라고 하면 어떻게 될까?
세그먼트 트리 + Lazy Propagation
백준 10999번: 구간 합 구하기 2 해당 문제를 풀이하면서 lazy propagation에 대해 알아보자.
일반적인 구간 합 문제는 세그먼트 트리를 사용하여 그냥 풀면 되지만 갱신하는 부분이 업그레이드되었다. 구간을 업데이트해준 다음 구간 합을 구해야한다. 단순 세그먼트 트리만으로 풀이를 하게 되면 업데이트 처리를 할 때, 최악의 경우 트리 전체를 업데이트 해줘야하기 때문에 O(NM + KlogN)의 시간이 걸린다. 범위가 크게 주어질 경우 이 풀이는 시간초과가 발생하게 된다.
그래서 lazy propagation을 사용해줘야 한다.
lazy propagaion은 처리를 미뤘다가 필요할 때 갱신을 해주는 방식이다. 빠른 처리를 위해 필요한 노드만 업데이트 처리를 해주고 나머지 자식 노드는 lazy상태를 걸어두었다가 나중에 필요해질 때(구간 합 구할 때) 업데이트를 처리해주는 방식이다. 이렇게 되면 최적화 방식으로 줄일 수 있기 때문에 일반 구간합을 구하는 시간복잡도와 마찬가지로 O((M+K)logN)로 쿼리를 해결할 수 있다.
이제 세그먼트 트리 로직에 lazy propagation을 어떻게 입히는지 살펴보자
propagate
- 해당 노드 lazy가 등록되어있으면 업데이트해준다.
- 리프노드인 경우 물려줌은 패스
- 리프노드가 아닌 경우 자식 노드들에게 lazy를 물려준다. (나중에 필요하게 될 때가 오면 갱신; 구간 합 구하는 로직)
- 해당 노드는 이제 업데이트 처리를 해준다. 노드 += 업데이트 값 * 해당 자식노드의 총 갯수
- ex) update 1 1 3 -3 : 1~3구간에 속하는 노드가 -3으로 업데이트된다면 1~3구간에 속하는 노드는 3*-3 = -9를 갱신해줘야한다.
- 업데이트 완료 후 해당 노드 lazy값을 삭제한다. lazy[node] =0;
코드
static void propagate(int start, int end, int node) {
// 값이 들어있는 경우 업데이트 처리 시작
if(lazy[node] !=0){
// 리프노드가 아닌 경우 자식에게 lazy 물려줌(자식은 나중에 갱신)
if(start != end) {
lazy[node*2] += lazy[node];
lazy[node*2 +1] += lazy[node];
}
tree[node] += lazy[node] * (end-start+1); // tree[node] = 업데이트 값 * 해당 자식노드의 총 갯수
lazy[node] = 0; // 업데이트 완료 후 초기화
}
}
update
- 조회하는 해당 노드에 lazy가 걸려있으면 propagate 메소드로 이동하여 갱신해준다. propagate(start, end, node);
- 업데이트 구간에 들어오게 되면 lazy를 등록해준다. if(left <= start && end <= right) { lazy[node] = dif; }
- 여기서 중요! 해당 노드만 바로 업데이트 처리해주고 바로 리턴한다. 자식 노드들은 나중에 필요할 때 갱신하게 lazy만 걸어주고 내버려두는게 포인트이다. propagate(start, end, node); return;
- 1~2번의 업데이트 로직이 모두 일어난 후 갱신된 노드들의 부모 노드에 반영해준다. tree[node] = tree[node*2]+tree[node*2+1];
코드
static void update(int start, int end, int node, int left, int right, long dif) {
propagate(start, end, node); // 해당 노드에 갱신할 값이 있다면 업데이트
if(end < left || right < start) return;
if(left <= start && end <= right) {
lazy[node] = dif; // 범위에 속할 경우 업데이트 lazy값 갱신
propagate(start, end, node); // 해당 노드에 갱신할 값이 있다면 업데이트
return;
}
int mid = (start+end)/2;
update(start, mid, node*2, left, right, dif);
update(mid+1, end, node*2+1, left, right, dif);
// update가 다 일어난 후 부모 노드에 반영
tree[node] = tree[node*2]+tree[node*2+1];
}
pSum
구간합을 구하는 데 방문하는 노드가 lazy가 걸려있다면 이 때 업데이트 처리를 해주게 된다.
- 조회하는 해당 노드에 lazy가 걸려있으면 propagate 메소드로 이동하여 갱신해준다. propagate(start, end, node);
- 업데이트된 노드로 구간합을 구해준다.
코드
static long pSum(int start, int end, int node, int left, int right) {
propagate(start, end, node); // // 해당 노드에 갱신할 값이 있다면 업데이트
if(end < left || right < start) return 0;
if(left <= start && end <= right) { // left ~ right 구간합 구하기
return tree[node];
}
int mid = (start+end)/2;
return pSum(start, mid, node*2, left, right) + pSum(mid+1, end, node*2+1, left, right);
}
시뮬레이션
이제 로직을 다 이해했으니 예제를 통해 시뮬레이션을 돌려보자.
주어진 배열 [1 2 3 4 5]로 세그먼트 트리를 초기화하면 다음과 같다.
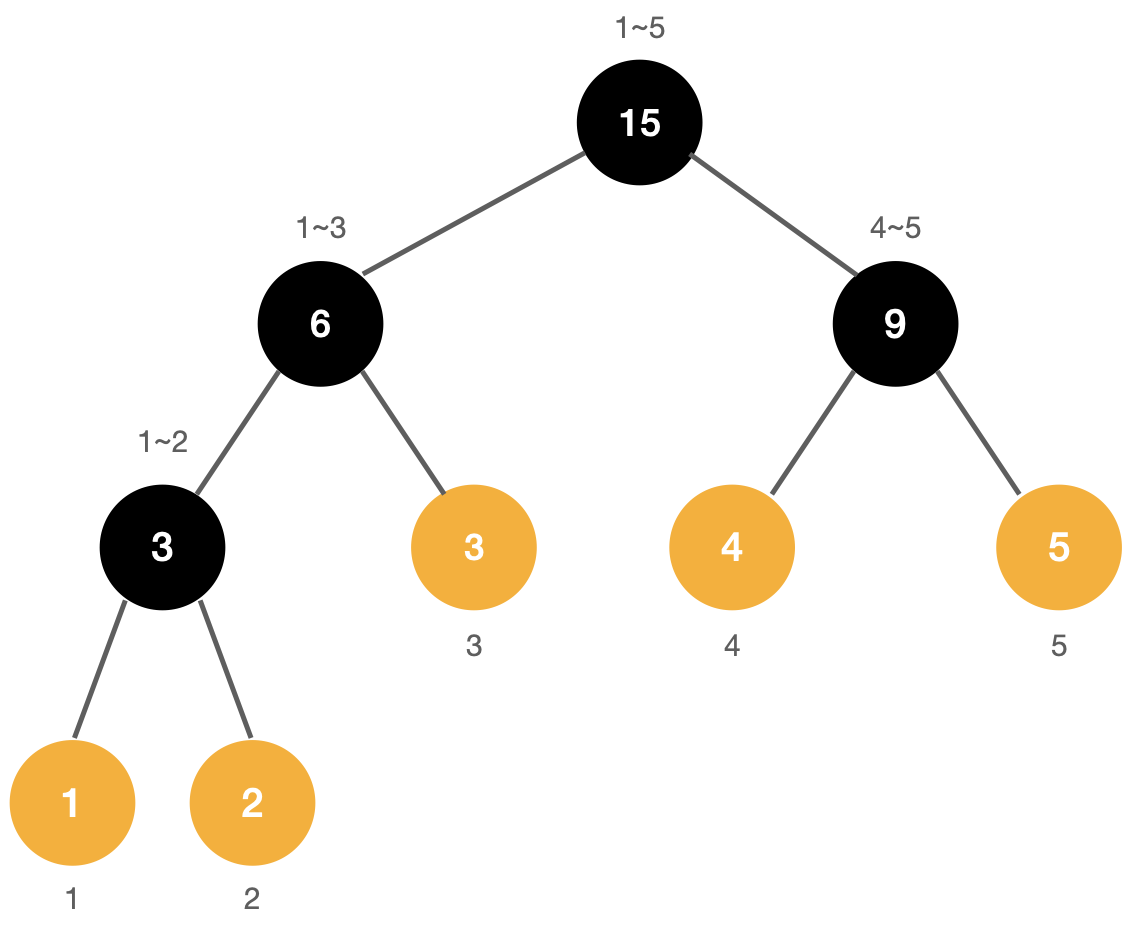
update 1 3 4 6
구간[3,4]에 속한 노드의 값을 +6 갱신해준다.

구간 3과 4에 속하는 리프노드들이 각 propagate(3,3,5), propagate(4,4,6)로직을 처리하는데 해당 노드들은 리프노드라서 lazy를 물려줄 자식이 없어서 물려줌없이 갱신만 되었다.
그 다음 tree[node] = tree[node*2]+tree[node*2+1]; 을 통해 부모노드들에게 갱신된 값을 처리해주고 연산은 끝이 났다. 이번 업데이트는 운좋게 각 노드들이 바로 리프노드에 걸려서 lazy처리된 부분이 없으므로 구간 합 구하는 부분은 넘어간다.
update 1 1 3 -2
구간[1,3]에 속한 노드의 값을-2 갱신해준다.

해당 update처리에서는 1~3의 구간이 2번노드에 딱 걸리게 되어서 propagation(1,3,2)을 처리해주고 update 처리는 종료된다.
이 때 propagation로직에서 자식노드들(4,5)에게 lazy를 물려주었다. (start!=end)
그 다음 tree[node] = tree[node*2]+tree[node*2+1];을 통해 부모노드인 1번노드를 갱신해주었다. lazy에 저장된 값들은 나중에 연산이 필요할 때 꺼내어 갱신하게 된다.
pSum 2 2 5
구간[2,5]의 합을 구해야한다.
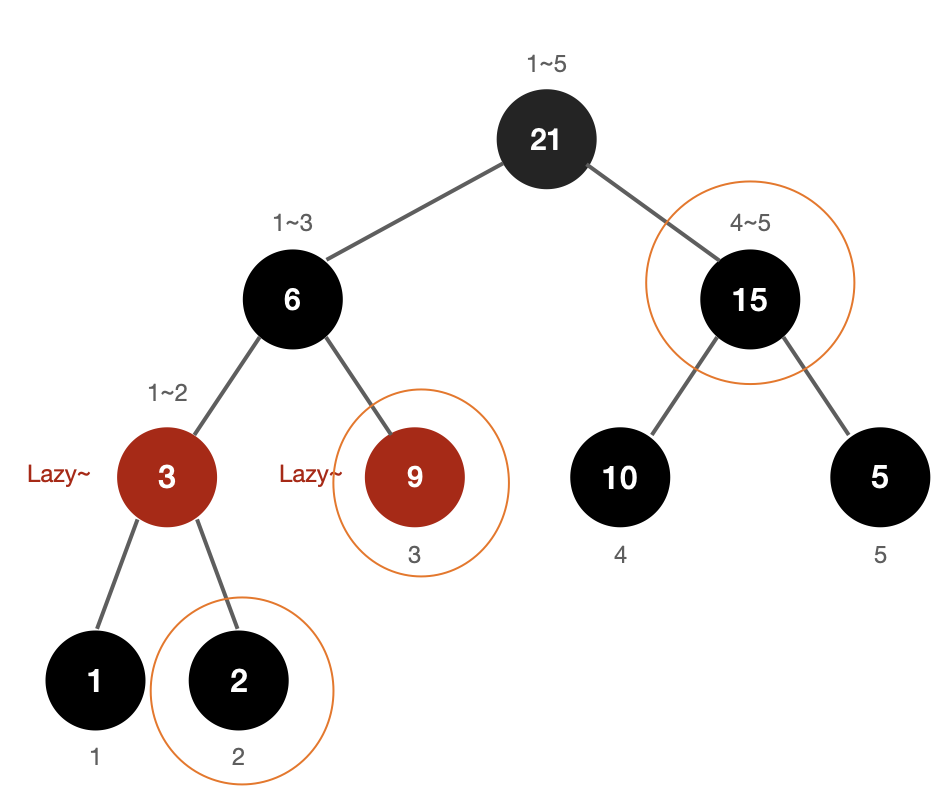
구간합을 구하기 위해서 pSum로직을 통해 해당 주황 동그라미를 친 노드(3, 5, 9)들을 방문해야 한다. 그러기 위해서는 현재 lazy가 걸려있는 4, 5번 노드를 거쳐야하므로 업데이트를 해줘야한다. 만약 [4,5]구간에서의 구간합을 구하는 거였다면 해당 lazy노드들은 이번 단계에서도 업데이트가 되지않고 lazy상태로 머물러있게 되었을 것이다.
따라서 pSum로직에 있는 propagation메소드를 통해 4,5번 lazy노드들 업데이트를 진행해준다.

lazy가 걸려있던 4,5번 노드를 갱신해주고 자식노드(8,9)에게 lazy를 물려준다. 그리고 pSum로직이 또 계산을 위해 9번 노드를 조회하여야 하므로 해당 층에 lazy가 걸려있는 8,9번 노드를 모두 갱신해준다.

이렇게 구간[2,5] = 0 +7 + 15 = 22를 구할 수 있게된다.
풀이 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int n;
static long[] elements, tree, lazy;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
elements = new long[n];
for(int i=0; i<n; i++) {
elements[i] = Long.parseLong(br.readLine());
}
int treeSize = getTreeSize();
tree = new long[treeSize];
lazy = new long[treeSize];
init(0,n-1,1);
for(int i=0; i<m+k; i++) {
st = new StringTokenizer(br.readLine());
int op = Integer.parseInt(st.nextToken());
int l = Integer.parseInt(st.nextToken())-1;
int r = Integer.parseInt(st.nextToken())-1;
if(op==1) {
long dif = Long.parseLong(st.nextToken());
update(0,n-1, 1, l, r, dif);
}else {
bw.write(pSum(0, n-1, 1, l, r)+"\n");
}
}
bw.flush();
bw.close();
}
static int getTreeSize() {
int h = (int)Math.ceil(Math.log(n)/Math.log(2)) +1;
return (int)Math.pow(2, h)-1;
}
static long init(int start, int end, int node) {
if(start == end) return tree[node] = elements[start];
int mid = (start+end)/2;
return tree[node] = init(start, mid, node*2) +init(mid+1, end, node*2+1);
}
static void propagate(int start, int end, int node) {
if(lazy[node] !=0){
if(start != end) {
lazy[node*2] += lazy[node];
lazy[node*2 +1] += lazy[node];
}
tree[node] += lazy[node] * (end-start+1);
lazy[node]=0;
}
}
static void update(int start, int end, int node, int left, int right, long dif) {
propagate(start, end, node);
if(end < left || right < start) return;
if(left <= start && end <= right) {
lazy[node] = dif;
propagate(start, end, node);
return;
}
int mid = (start+end)/2;
update(start, mid, node*2, left, right, dif);
update(mid+1, end, node*2+1, left, right, dif);
tree[node] = tree[node*2]+tree[node*2+1];
}
static long pSum(int start, int end, int node, int left, int right) {
propagate(start, end, node);
if(end < left || right < start) return 0;
if(left <= start && end <= right) return tree[node];
int mid = (start+end)/2;
return pSum(start, mid, node*2, left, right) + pSum(mid+1, end, node*2+1, left, right);
}
}'Dot Algo∙ DS > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘] 가장 긴 증가하는 부분 수열 LIS - DP & 이진탐색 (Java) (2) | 2021.08.09 |
|---|---|
| [알고리즘] 최소 공통 조상 LCA 트리 - DP & 세그먼트 트리 (Java) (2) | 2021.08.04 |
| [알고리즘] 투 포인터와 슬라이딩 윈도우 (Java) (0) | 2021.07.07 |
| [알고리즘] 순열, 조합 알고리즘 정리 (Java) (0) | 2021.06.22 |
| [알고리즘] 외판원 순회 문제(TSP: Travelling Salesman Problem) 정리 (Java) (0) | 2021.06.15 |




