#1149 RGB거리
난이도 : 실버 1
유형 : DP
9466번: 텀 프로젝트
이번 가을학기에 '문제 해결' 강의를 신청한 학생들은 텀 프로젝트를 수행해야 한다. 프로젝트 팀원 수에는 제한이 없다. 심지어 모든 학생들이 동일한 팀의 팀원인 경우와 같이 한 팀만 있을
www.acmicpc.net
▸ 문제
RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다.
집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자.
- 1번 집의 색은 2번 집의 색과 같지 않아야 한다.
- N번 집의 색은 N-1번 집의 색과 같지 않아야 한다.
- i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.
▸ 입력
첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 같은 자연수이다.
▸ 출력
첫째 줄에 모든 집을 칠하는 비용의 최솟값을 출력한다.
문제 풀이
해당 풀이는 2가지 접근이 가능하다.
- 트리 후위순회 탐색으로 N번집부터 시작하여 1번집까지 하향식으로 탐색하여 최소 비용 구하기
- 점화식을 세워 1~N번집을 순차적으로 반복하여 최소 비용 구하기
간단한 것은 2번 일반 DP풀이가 훨씬 간단하지만 후에 응용에 있어서 숙련도를 쌓고자 트리 DP방식으로도 풀이를 해봤다.
설계
- N번의 집(루트 노드)를 시작으로 트리 후위 탐색을 시작한다.
- 상위(pos) 집이 칠한 색을 제외한 나머지 색을 탐색한다. if(color != i)
- 이 중 최소의 비용을 갖는 자식 집(child)의 값을 구한다. Math.min(value, dp[child][i]);
- 자식 집 중 최소 비용을 상위 집에 더해준다. dp[pos][color] = cost[pos][color] + value;
- 위에서 저장한 비용은 자식 집이 변하지 않는 이상 고정이므로 중복되는 연산은 제거해준다. if(dp[pos][color] != 0) return;
- N번집까지 계산을 마친 후 최소 비용을 출력해준다.
시뮬레이션

이를 후위 탐색으로 1번 집부터 최소 비용을 골라 상위 집에 더해주면 최종적으로 3번 집에 최소 비용을 모두 합한 값을 얻을 수 있다.
1) 3번 집을 빨간색으로 칠할 경우
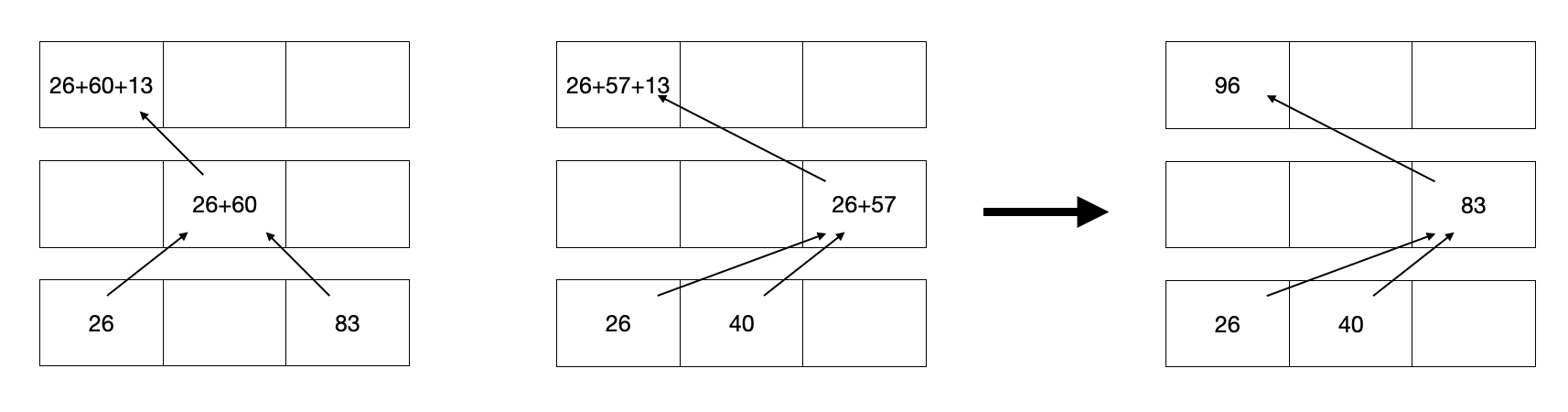
2) 3번 집을 초록색으로 칠할 경우

3) 3번 집을 파랑색으로 칠할 경우

따라서 이 중 최솟값을 구하면 답은 96이 되는 것을 알 수 있다.
풀이 코드 (트리 DP)
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int n;
static int[][] dp, cost;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
cost = new int[n][3];
dp = new int[n][3];
StringTokenizer st = null;
for(int i=0; i<n; i++) {
st = new StringTokenizer(br.readLine());
for(int j=0; j<3; j++) {
cost[i][j] = Integer.parseInt(st.nextToken());
}
}
for(int i=0; i<3; i++) {
dp[0][i] = cost[0][i];
}
for(int i=0; i<3; i++) {
solve(n-1, i);
}
int res = Integer.MAX_VALUE;
for(int i=0; i<3; i++) {
res = Math.min(res, dp[n-1][i]);
}
System.out.print(res);
}
static void solve(int pos, int color) {
if(pos ==0) return;
if(dp[pos][color] != 0) return;
int child = pos-1;
int value = Integer.MAX_VALUE;
for(int i=0; i<3; i++) {
if(color != i) {
solve(child, i);
value = Math.min(value, dp[child][i]);
}
}
dp[pos][color] = cost[pos][color] + value;
}
}
풀이 코드 (일반 DP)
점화식을 통해 푸는 풀이도 위의 설계 구조와 다를 바 없다. 단지 최소 비용을 구하는 순서만 바뀔 뿐이다.
- 1번 집부터 N번 집까지 순차적으로 탐색한다.
- 현재의 집(i)의 색깔과 겹치지 않게 이전 집의 색칠 비용 중 최소의 값을 골라 현재 자신의 비용과 더해서 저장한다. dp[i][0] = Math.min(dp[i-1][1], dp[i-1][2]) + cost[i][0];
- N번집까지 계산을 마친 후 최소 비용을 출력해준다.
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int n;
static int[][] dp, cost;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
cost = new int[n][3];
dp = new int[n][3];
StringTokenizer st = null;
for(int i=0; i<n; i++) {
st = new StringTokenizer(br.readLine());
for(int j=0; j<3; j++) {
cost[i][j] = Integer.parseInt(st.nextToken());
}
}
for(int i=0; i<3; i++) {
dp[0][i] = cost[0][i];
}
for(int i=1; i<n; i++) {
dp[i][0] = Math.min(dp[i-1][1], dp[i-1][2]) + cost[i][0];
dp[i][1] = Math.min(dp[i-1][0], dp[i-1][2])+ cost[i][1];
dp[i][2] = Math.min(dp[i-1][0], dp[i-1][1])+ cost[i][2];
}
int res = Integer.MAX_VALUE;
for(int i=0; i<3; i++) {
res = Math.min(res, dp[n-1][i]);
}
System.out.print(res);
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 1932번 정수 삼각형 (Java) (0) | 2021.08.20 |
|---|---|
| [BOJ] 백준 2250번 트리의 높이와 너비 (Java) (0) | 2021.08.19 |
| [BOJ] 백준 11726 2xn 타일링 (Java) (0) | 2021.08.18 |
| [BOJ] 백준 1275 커피숍2 (Java) (0) | 2021.08.17 |
| [BOJ] 백준 1003번 피보나치 함수 (Java) (0) | 2021.08.16 |




