#2268 수들의 합 7
난이도 : 골드 1
유형 : 펜윅 트리
2268번: 수들의 합 7
첫째 줄에는 N(1 ≤ N ≤ 1,000,000), M(1 ≤ M ≤ 1,000,000)이 주어진다. M은 수행한 명령의 개수이며 다음 M개의 줄에는 수행한 순서대로 함수의 목록이 주어진다. 첫 번째 숫자는 어느 함수를 사용했는
www.acmicpc.net
▸ 문제
N개의 수 A[1], A[2], …, A[N] 이 주어졌을 때, 함수 Sum(i, j)는 A[i] + A[i+1] + … + A[j]를 구하는 함수이다. (i > j일 경우에는 A[j] + A[j+1] + ... + A[i]) A가 주어졌을 때, Sum(i, j)를 구하는 것은 매우 쉬운 문제이다. 이러한 (i, j)가 여러 개 주어졌을 때도 별로 어려운 문제는 아니다.
Sum함수와 더불어 Modify라는 함수를 정의하자. Modify(i, k)를 수행하면 A[i] = k가 되는 함수이다. Sum함수와 Modify 함수의 사용 목록이 주어졌을 때, 이에 해당하는 연산을 하는 프로그램을 작성하시오. 두 함수를 섞어서 사용할 수도 있다.
▸ 입력
첫째 줄에는 N(1 ≤ N ≤ 1,000,000), M(1 ≤ M ≤ 1,000,000)이 주어진다. M은 수행한 명령의 개수이며 다음 M개의 줄에는 수행한 순서대로 함수의 목록이 주어진다. 첫 번째 숫자는 어느 함수를 사용했는지를 나타내며, 0일 경우에는 Sum 함수를, 1일 경우에는 Modify 함수를 나타낸다. 다음 두 수는 각 함수의 인자 (i, j)나 (i, k)를 나타낸다. 처음에는 A[1] = A[2] = … = A[N] = 0이다. Modify인 경우에 1 ≤ k ≤ 100,000 이다.
▸ 출력
Sum 함수의 개수만큼 각 줄에 Sum 함수의 리턴값을 출력한다.
i
문제 풀이
일반 세그먼트 트리로도 풀이할 수 있고 펜윅 트리로도 풀이할 수 있다. 보통 구간 합을 구하는 문제는 펜윅트리 구현이 더 간단하기 때문에 이를 이용하는 게 좋다.
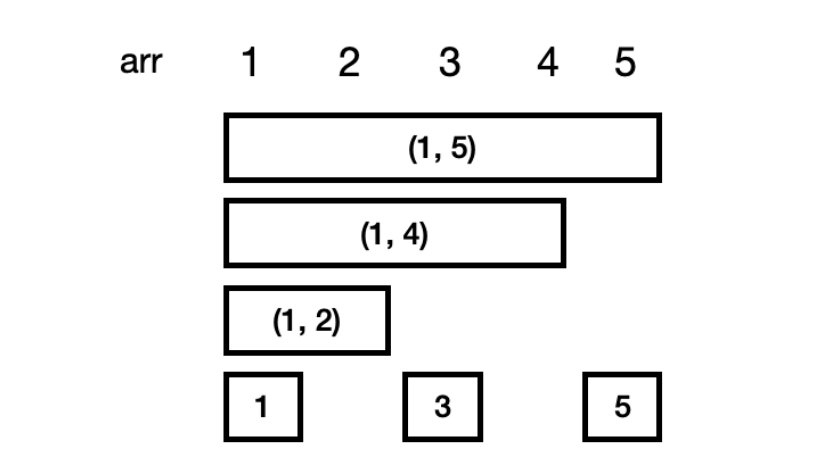
1. 배열 값 변경하기
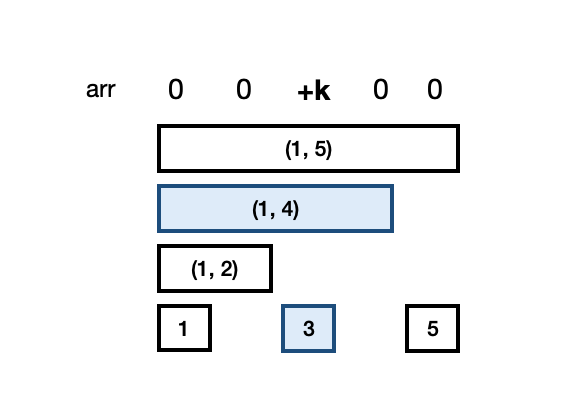
arr[pos]값을 +k를 해줘야 한다. 펜웍트리에서 배열 값을 변경하는 것은 해당 위치의 값에 숫자를 더하고 빼는 것으로 구현한다. 맨 오른쪽에 있는 1인 비트를 스스로에게 더해주는 연산을 반복하여 해당 위치를 포함하는 구간들을 모두 만날 수 있다.
만약 구간 3에 +k를 한다면 다음과 같다. arr[3]을 포함하는 모든 구간의 합을 k씩 늘려주면 된다.
- 이때 늘려줘야 할 값들은 3번 노드, 4번 노드 로 이진수로 표현하면 11(2) → 100(2)로 이동한다.
- pos += (pos&-pos);
2. 구간 합 구하기
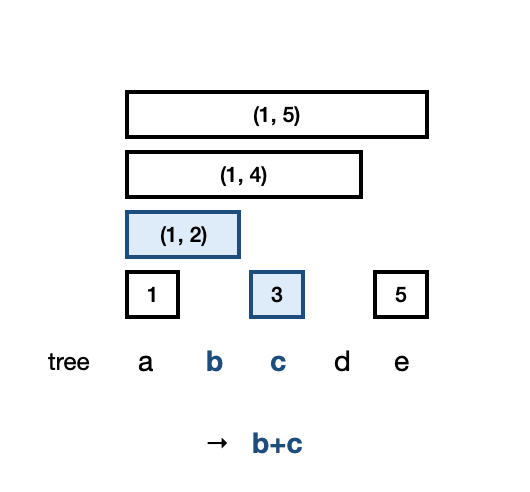
i부터 j까지의 구간 합을 구하려면 psum[j] - psum[i-1]의 값을 구해주면 된다. psum의 값은 오른쪽 끝 위치의 이진수 표현에서 마지막 비트를 지우면 다음 구간을 쉽게 찾을 수 있다.
예를 들어 psum[3]을 구하기 위해 더해야 하는 숫자는 3에서 끝나는 구간의 합 3번 노드, 2에서 끝나는 구간의 합 tree[2]이다.
- 3번 노드, 2번 노드를 이진수로 표현하면 11(2) → 10(2)이다.
- pos &= (pos-1);
풀이 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int[] arr;
static long[] tree;
static int n;
static void add(int pos, long val) {
while(pos <= n) {
tree[pos] += val;
pos += (pos&-pos);
}
}
static long sum(int pos) {
long result = 0;
while(pos > 0) {
result += tree[pos];
pos &= (pos-1);
}
return result;
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
arr = new int[n+1];
tree = new long[n+1];
StringBuilder sb = new StringBuilder();
for(int i=0; i<m; i++) {
st = new StringTokenizer(br.readLine());
int op = Integer.parseInt(st.nextToken());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
if(op == 0) {
if(b < a) {
int tmp = a;
a = b;
b = tmp;
}
sb.append(sum(b)-sum(a-1)+"\n");
}else {
long dif = b - arr[a];
arr[a] = b;
add(a, dif);
}
}
System.out.println(sb.toString());
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 7578번 공장 (Java) (0) | 2022.01.07 |
|---|---|
| [BOJ] 백준 14438번 수열과 쿼리 17 (Java) (0) | 2022.01.06 |
| [BOJ] 백준 16975번 수열과 쿼리 21 (Java) - Fenwick (0) | 2022.01.04 |
| [BOJ] 백준 11377번 열혈강호 3 (Java) (0) | 2022.01.03 |
| [BOJ] 백준 11376번 열혈강호 2 (Java) (0) | 2022.01.02 |




