#7578 공장
난이도 : 플레 5
유형 : 펜윅 트리
7578번: 공장
어떤 공장에는 2N개의 기계가 2열에 걸쳐 N개씩 배치되어 있다. 이 2개의 열을 각각 A열과 B 열이라고 부른다. A열에 있는 N개의 기계는 각각이 B열에 있는 N개의 기계와 하나씩 짝을 이루어 케이블
www.acmicpc.net
▸ 문제
어떤 공장에는 2N개의 기계가 2열에 걸쳐 N개씩 배치되어 있다. 이 2개의 열을 각각 A열과 B 열이라고 부른다. A열에 있는 N개의 기계는 각각이 B열에 있는 N개의 기계와 하나씩 짝을 이루어 케이블로 연결되어 있다. 즉, A열의 임의의 기계는 B열의 유일한 기계와 케이블로 연결되어 있고, B열의 임의의 기계는 A열의 유일한 기계와 케이블로 연결되어 있다
또한, 각 기계에는 식별번호가 붙어있으며, 짝이 맺어진 기계끼리는 같은 식별번호가 붙어있다. 즉, 각 열에 있는 N개의 기계끼리는 서로 다른 식별번호를 가지고 있으며, 반대쪽 열에 있는 같은 식별번호를 가진 기계와 케이블로 이어져 있다.
공장 작업의 효율성을 위해 기계들은 짝을 맺은 순서대로 배치되지 않으며, 필요에 따라 각 열의 기계들의 순서를 바꾼 바람에 케이블은 마구 엉켜있는 상태이다. 이렇게 엉켜버린 케이블은 잦은 고장의 원인이 되기 때문에, 기계의 위치를 바꾸지 않은 상태에서 케이블을 두 기계를 잇는 직선의 형태로 만들기로 했다.

예를 들어, 위의 그림과 같이 N = 5이고, A열에 위치한 기계의 식별번호가 순서대로 132, 392, 311, 351, 231이고 B열에 위치한 기계의 식별번호가 순서대로 392, 351, 132, 311, 231이라면 케이블들의 교차 횟수 혹은 서로 교차하는 케이블 쌍의 개수는 3이 된다.
정수 N과 A열에 위치한 기계, B열에 위치한 기계의 식별번호가 각각 순서대로 주어질 때에 서로 교차하는 케이블 쌍의 개수를 정확하게 세어 출력하는 프로그램을 작성하시오.
▸ 입력
입력은 세 줄로 이루어져 있다. 첫 줄에는 정수 N이 주어지며, 두 번째 줄에는 A열에 위치한 N개 기계의 서로 다른 식별번호가 순서대로 공백문자로 구분되어 주어진다. 세 번째 줄에는 B열에 위치한 N개의 기계의 식별번호가 순서대로 공백문자로 구분되어 주어진다.
단, 1 ≤ N ≤ 500,000이며, 기계의 식별번호는 모두 0 이상 1,000,000 이하의 정수로 주어진다.
▸ 출력
여러분은 읽어 들인 2N개의 기계의 배치로부터 서로 교차하는 케이블 쌍의 개수를 정수 형태로 한 줄에 출력해야 한다.
문제 풀이
Inversion counting 문제로 해당 풀이를 참고하였습니다. 펜윅트리나 세그먼트 트리를 이용해 O(nlogn)으로 풀이가 가능합니다.
arr[1 ... n] 배열이 있을 때, 반전된 쌍은 (i, j)가 i < j 이면서 arr[i] > arr[j]인 경우를 뜻한다.
n+1의 크기를 가진 tree 배열을 만들고 tree[i]는 [1, i]까지 연결된 선분의 수를 나타낸다. 그리고 arr[j]는 j가 연결된 위치라고 할때, j를 인덱스로 반복문을 돌리면서 arr[j]값을 통해 답을 도출해낼 수 있다.
- update(arr[j]) tree의 arr[j]에 해당하는 인덱스에 +1을 더해준다. [1, arr[j]]까지 연결된 수를 효율적으로 카운팅해준다.
- j-sum(arr[j])를 반전 쌍의 갯수에 더해준다.
시뮬레이션
위의 예제를 통해 arr을 구하면 (1, 3), (2, 1), (3, 4), (4, 2), (5,5)가 된다 이를 통해 시뮬레이션를 돌려보자.
j는 현재 노드까지 연결된 선분의 수, sum(arr[j])는 [1, j]까지 연결된 선분의 수이므로 j - sum(arr[j])로 Inversion counting을 할 수 있다.
- 이 풀이는 A의 관점에서 풀이를 하였고 다른 방식으로 B의 관점으로 풀어도 된다. B의 관점에서 풀면, (1, 2), (2,4), (3,1), (4,3), (5,5)로 데이터가 주어진다.
1. j=1 , arr[j] = 3
- 1 - sum(3) = 0 이므로, 반전된 수는 0개이다.

2. j=2, arr[j] = 1
- 2 - sum(1) = 1 이므로, 반전된 수 1개를 카운팅해준다.

3. j=3, arr[j] = 4
- 3 - sum(4) = 0 이므로, 반전된 수는 0개이다.

4. j=4, arr[j] = 2
- 4 - sum(2) = 2 이므로, 반전된 수 2개를 카운팅해준다.
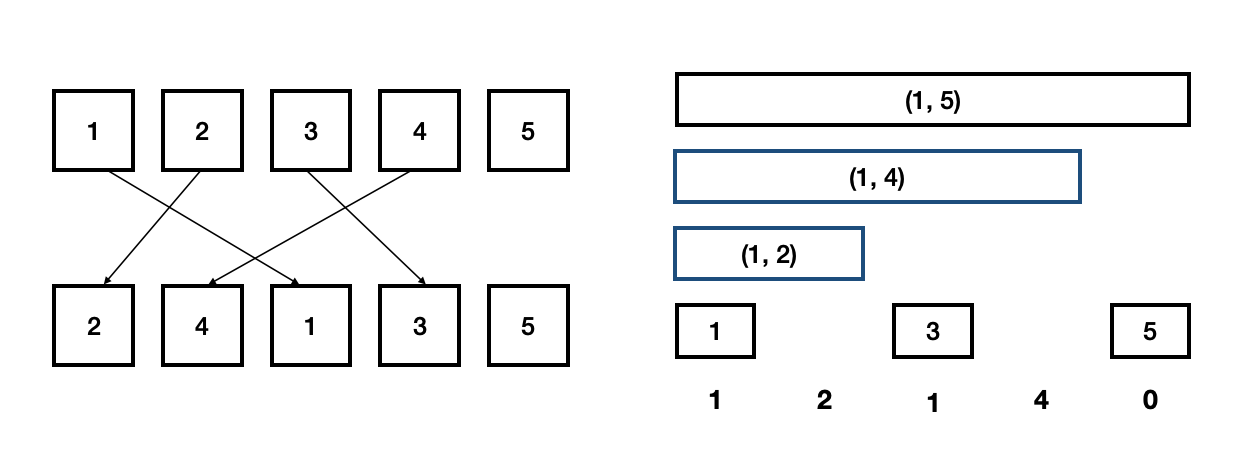
3. j=5, arr[j] = 5
- 5 - sum(5) = 0 이므로, 반전된 수는 0이다.
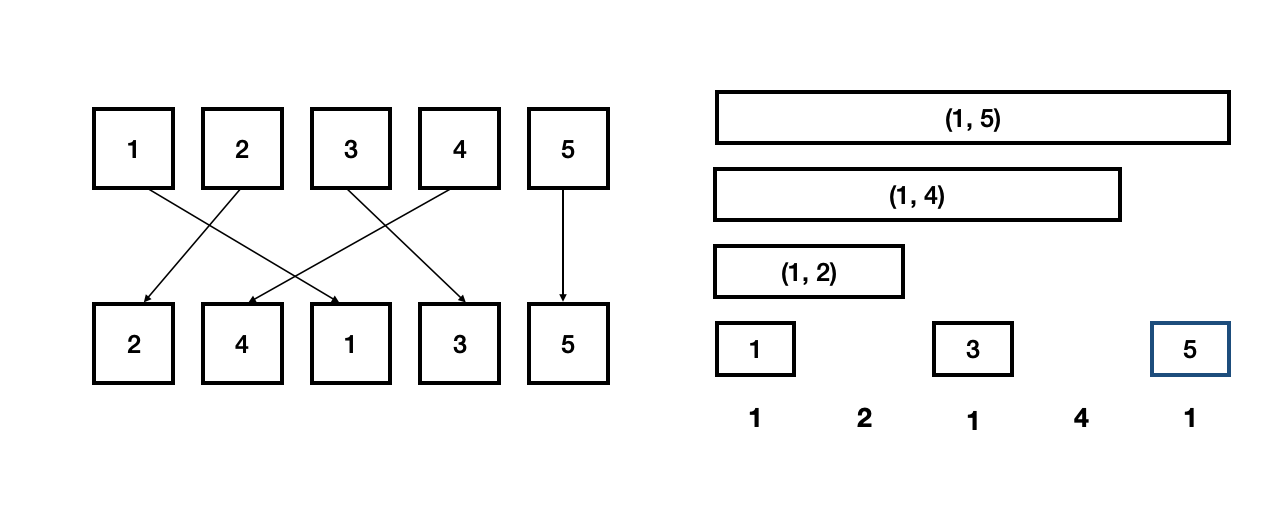
따라서, 총 반전된 수는 3개임을 알 수 있다.
풀이 코드
import java.io.*;
import java.util.*;
public class Main {
static int n;
static long[] tree;
static long sum(int idx) {
long res = 0;
while(idx > 0) {
res += tree[idx];
idx &= (idx - 1);
}
return res;
}
static void update(int idx) {
while(idx <= n) {
tree[idx] += 1;
idx += (idx & -idx);
}
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
Map<Integer, Integer> first = new HashMap<>();
Map<Integer, Integer> second = new TreeMap<>();
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=1; i<=n; i++) {
first.put(Integer.parseInt(st.nextToken()), i);
}
st = new StringTokenizer(br.readLine());
for(int i=1; i<=n; i++) {
second.put(first.get(Integer.parseInt(st.nextToken())), i);
}
tree = new long[n+1];
long answer = 0;
for(int key: second.keySet()) {
int num = second.get(key);
update(num);
answer += (key-sum(num));
}
System.out.println(answer);
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 2517번 달리기 - 펜윅, 세그먼트 (Java) (1) | 2022.01.09 |
|---|---|
| [BOJ] 백준 2243번 사탕상자 (Java) (0) | 2022.01.08 |
| [BOJ] 백준 14438번 수열과 쿼리 17 (Java) (0) | 2022.01.06 |
| [BOJ] 백준 2268번 수들의 합 7 (Java) (0) | 2022.01.05 |
| [BOJ] 백준 16975번 수열과 쿼리 21 (Java) - Fenwick (0) | 2022.01.04 |




