#2517 달리기
난이도 : 플레 4
유형 : 세그먼트 트리 / 펜윅 트리
2517번: 달리기
첫째 줄에는 선수의 수를 의미하는 정수 N이 주어진다. N은 3 이상 500,000 이하이다. 이후 N개의 줄에는 정수가 한 줄에 하나씩 주어진다. 이 값들은 각 선수들의 평소 실력을 앞에서 달리고 있는
www.acmicpc.net
▸ 문제
KOI 장거리 달리기 대회가 진행되어 모든 선수가 반환점을 넘었다. 각 선수의 입장에서 자기보다 앞에 달리고 있는 선수들 중 평소 실력이 자기보다 좋은 선수를 남은 거리 동안 앞지르는 것은 불가능하다. 반대로, 평소 실력이 자기보다 좋지 않은 선수가 앞에 달리고 있으면 남은 거리 동안 앞지르는 것이 가능하다. 이러한 가정 하에서 각 선수는 자신이 앞으로 얻을 수 있는 최선의 등수를 알 수 있다.
각 선수의 평소 실력은 정수로 주어지는데 더 큰 값이 더 좋은 실력을 의미한다. 현재 달리고 있는 선수를 앞에서 부터 표시했을 때 평소 실력이 각각 2, 8, 10, 7, 1, 9, 4, 15라고 하면 각 선수가 얻을 수 있는 최선의 등수는 (같은 순서로) 각각 1, 1, 1, 3, 5, 2, 5, 1이 된다. 예를 들어, 4번째로 달리고 있는 평소 실력이 7인 선수는 그 앞에서 달리고 있는 선수들 중 평소 실력이 2인 선수만 앞지르는 것이 가능하고 평소실력이 8과 10인 선수들은 앞지르는 것이 불가능하므로, 최선의 등수는 3등이 된다.
선수들의 평소 실력을 현재 달리고 있는 순서대로 입력 받아서 각 선수의 최선의 등수를 계산하는 프로그램을 작성하시오.
▸ 입력
첫째 줄에는 선수의 수를 의미하는 정수 N이 주어진다. N은 3 이상 500,000 이하이다. 이후 N개의 줄에는 정수가 한 줄에 하나씩 주어진다. 이 값들은 각 선수들의 평소 실력을 앞에서 달리고 있는 선수부터 제시한 것이다. 각 정수는 1 이상 1,000,000,000 이하이다. 단, 참가한 선수들의 평소 실력은 모두 다르다.
▸ 출력
각 선수의 최선의 등수를 나타내는 정수 N개를 입력에 주어진 선수 순서와 동일한 순서로 한 줄에 하나씩 출력한다.
문제 풀이
최대 50만 플레이어의 등수를 비교하는 문제로 선형으로 하면 시간초과가 발생한다. 그래서 세그먼트 트리 자료구조를 사용하여 로그 시간이 걸리는 쿼리로 풀이를 해줘야 한다.
기본적인 아이디어는 간단하다. 순차대로 선수들의 등수를 입력받는다. 그리고 현재 있는 플레이어 수 중에 자신이 몇등인지 계산해주면 된다.

펜윅 트리로 구현하기
현재 들어있는 선수의 수, 그 중 자신의 능력보다 낮은 선수의 수를 계산해주면 된다. 펜윅트리에는 순차대로 각 선수의 능력에 해당하는 인덱스에 값을 추가해주면 된다.
- 최선 등수 = 현재 들어있는 선수 총합 - 자신의 능력보다 낮은 선수의 수
- 펜윅트리 자료구조에는 능력을 기준으로 값을 저장한다.
- 능력 순위 간격은 일정하지 않기 때문에 좌표압축은 필수이다.
좌표압축하면 선수들의 능력은 2, 5, 7, 4, 1, 6, 3, 8 이 된다. 이를 통해 시뮬레이션을 돌려보자.
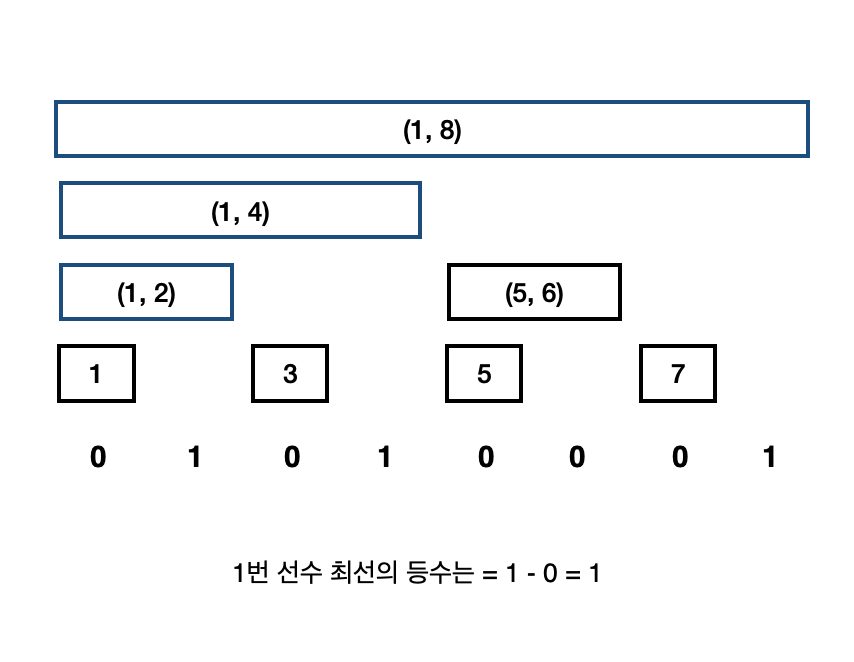
1번 선수 입장 (능력 2)
- 처음 1번 선수의 능력은 2이므로 해당 인덱스의 값을 +1 올려준다.
- 현재 들어있는 선수의 수 : 1, 2의 능력보다 낮은 선수의 수는 0이므로 최선의 등수는 1등이다.
2번 선수 입장 (능력 5)
- 2번 선수의 능력은 5이므로 해당 인덱스의 값을 +1 올려준다.
- 현재 들어있는 선수의 수 : 2, 5의 능력보다 낮은 선수의 수는 1명 있으므로 최선의 등수는 1등이다.

3번 선수 입장 (능력 7)
- 3번 선수의 능력은 7이므로 해당 인덱스의 값을 +1 올려준다.
- 현재 들어있는 선수의 수 : 3, 7의 능력보다 낮은 선수의 수는 2명 있으므로 최선의 등수는 1등이다.

4번 선수 입장 (능력 4)
- 3번 선수의 능력은 4이므로 해당 인덱스의 값을 +1 올려준다.
- 현재 들어있는 선수의 수 : 4, 4의 능력보다 낮은 선수의 수는 1명 있으므로 최선의 등수는 3등이다.

펜윅트리는 이와 같은 방식으로 계속해서 탐색해주면 된다.
세그먼트 트리로 구현하기
기존 세그먼트 트리 또한 방식은 똑같은데 저장 방식만 다르다. 가볍게만 살펴보자.
1번 선수 입장 (능력 2)
- 계산방식은 펜윅과 동일하다.
- 1번 선수의 능력은 2이므로 해당 인덱스의 값을 +1 올려준다.
- 현재 들어있는 선수의 수 :1, 2의 능력보다 낮은 선수의 수는 0명 있으므로 최선의 등수는 1등이다.

2번 선수 입장 (능력 5)
- 계산방식은 펜윅과 동일하다.
- 2번 선수의 능력은 5이므로 해당 인덱스의 값을 +1 올려준다.
- 현재 들어있는 선수의 수 : 2, 5의 능력보다 낮은 선수의 수는 1명 있으므로 최선의 등수는 1등이다.

이와 같은 방식으로 계속해서 연산을 이뤄나가면 된다.
💡 세그먼트트리에 대한 자세한 설명은 여기를 참고해주세요
💡 펜윅트리에 대한 자세한 설명은 여기를 참고해주세요
풀이 코드 - 펜윅 트리
import java.io.*;
import java.util.*;
public class Main {
static class Runner{
int idx;
int skill;
public Runner(int idx, int talent) {
this.idx = idx;
this.skill = talent;
}
}
static int n;
static int[] tree;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
List<Runner> runners = new ArrayList<>();
for(int i=0; i<n; i++) {
runners.add(new Runner(i, Integer.parseInt(br.readLine())));
}
Collections.sort(runners, (a,b)-> (a.skill - b.skill));
for(int i=0; i<runners.size(); i++) {
Runner runner = runners.get(i);
runner.skill = i+1;
}
Collections.sort(runners, (a,b)-> (a.idx - b.idx));
StringBuilder sb = new StringBuilder();
tree = new int[n+1];
for(int i=1; i<=n; i++) {
int skill = runners.get(i-1).skill;
sb.append(i - sum(skill-1) +"\n");
update(skill,1);
}
System.out.println(sb.toString());
}
static int sum(int idx) {
int result = 0;
while(idx > 0) {
result += tree[idx];
idx -= (idx & -idx);
}
return result;
}
static void update(int idx, int val) {
while(idx <= n) {
tree[idx] += val;
idx += (idx & -idx);
}
}
}
풀이 코드 - 세그먼트 트리
import java.io.*;
import java.util.*;
public class Main {
static class Runner{
int idx;
int skill;
public Runner(int idx, int talent) {
this.idx = idx;
this.skill = talent;
}
}
static int n;
static int[] tree;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
List<Runner> runners = new ArrayList<>();
for(int i=0; i<n; i++) {
runners.add(new Runner(i, Integer.parseInt(br.readLine())));
}
Collections.sort(runners, (a,b)-> (a.skill - b.skill));
for(int i=0; i<runners.size(); i++) {
Runner runner = runners.get(i);
runner.skill = i+1;
}
Collections.sort(runners, (a,b)-> (a.idx - b.idx));
StringBuilder sb = new StringBuilder();
tree = new int[n*4];
for(int i=1; i<=n; i++) {
int skill = runners.get(i-1).skill;
sb.append(i- query(1,n, 1, 1,skill) +"\n");
update(1,n,1, skill);
}
System.out.println(sb.toString());
}
static int query(int s, int e, int node, int l, int r) {
if(e < l || r < s) return 0;
if(l <= s && e <= r) {
return tree[node];
}
int mid = (s+e)/2;
return query(s, mid, node*2, l, r) + query(mid+1, e, node*2+1, l, r);
}
static int update(int s, int e, int node, int idx) {
if(idx < s || e < idx) return tree[node];
if(s == e) {
return tree[node] += 1;
}
int mid = (s+e)/2;
return tree[node] = update(s, mid, node*2, idx)+ update(mid+1, e, node*2+1, idx);
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 1395번 스위치 (Java) (0) | 2022.01.11 |
|---|---|
| [BOJ] 백준 3653번 영화 수집 (Java) (0) | 2022.01.10 |
| [BOJ] 백준 2243번 사탕상자 (Java) (0) | 2022.01.08 |
| [BOJ] 백준 7578번 공장 (Java) (0) | 2022.01.07 |
| [BOJ] 백준 14438번 수열과 쿼리 17 (Java) (0) | 2022.01.06 |




