균형잡힌 이진 검색 트리 (Balanced Binary Search Tree)
표준 라이브러리의 이진 검색 트리는 대부분 X보다 작은 원소의 수를 계산하거나 k번째 원소를 찾는 연산을 지원하지 않기 때문에 이진 검색 트리를 직접 구현해야 할 경우가 종종 있다. 단순한 이진 검색 트리는 특정 형태의 입력에 대해 편향트리와 같은 연결 리스트가 되어 버리는 문제가 있기 때문에, 균형잡힌 이진 검색 트리를 구현해야 한다.
AVL 트리나 레드 블랙 트리 등 교과서에 실리는 대부분의 균형잡힌 이진 검색 트리들은 구현이 매우 까다롭다. 다양한 경우의 수를 따져서 구현해야 하기 때문에 코드도 길고, 한정된 시간 안에 코드를 작성해야 하는 프로그래밍 대회에서 사용하기엔 부적합하다.
따라서 대회에서는 구현이 간단한 트립(treap)을 사용한다.
트립 (Treap)
트립은 입력이 특정 순서로 주어질 때 그 성능이 떨어진다는 이진 검색 트리의 단점을 해결하기 위해 고안된 일종의 랜덤화된 이진 검색 트리이다.
트립 성질
트립은 이진 검색 트리와 같은 성질을 가지고 있지만 트리의 형태가 원소들의 추가 순서에 따라 결정되지 않고 난수에 의해 임의대로 결정된다.
- 때문에 원소들이 어느 순서대로 추가되고 삭제되더라도 트리 높이의 기대치는 항상 일정하다.
- 이와 같은 속성을 유지하기 위해 트립은 새 노드가 추가될 때 마다 해당 노드에 우선순위(priority)를 부여한다. 이 우선순위는 원소의 대소 관계나 입력되는 순서와 아무런 상관 없이 난수를 통해 생성한다.
트립 두 가지 조건
트립은 항상 부모의 우선순위가 자식의 우선순위보다 높은 이진 검색 트리를 만든다. 따라서 트립의 조건을 다음 두 가지로 정의할 수 있다.
이진 검색 트리의 조건
- 모든 노드에 대해 왼쪽 서브트리에 있는 노드들의 원소는 해당 노드의 원소보다 작고, 오른쪽 서브트리에 있는 노드들의 원소는 해당 노드의 원소보다 크다.
힙의 조건
- 모든 노드의 우선순위는 각자의 자식 노드보다 크거나 같다.
랜덤화에 의한 트리 구조 개선 - 우선순위를 정하자
왼쪽(a)은 편향된 트리이고 오른쪽(b)은 우선순위 높은 것이 위로 오도록 노드들을 재배치한 결과이다. 모두 똑같은 원소들을 저장하지만 높이가 6이었던 (a)트리에 비해 훨씬 가로로 잘 퍼져있음을 볼 수 있다.
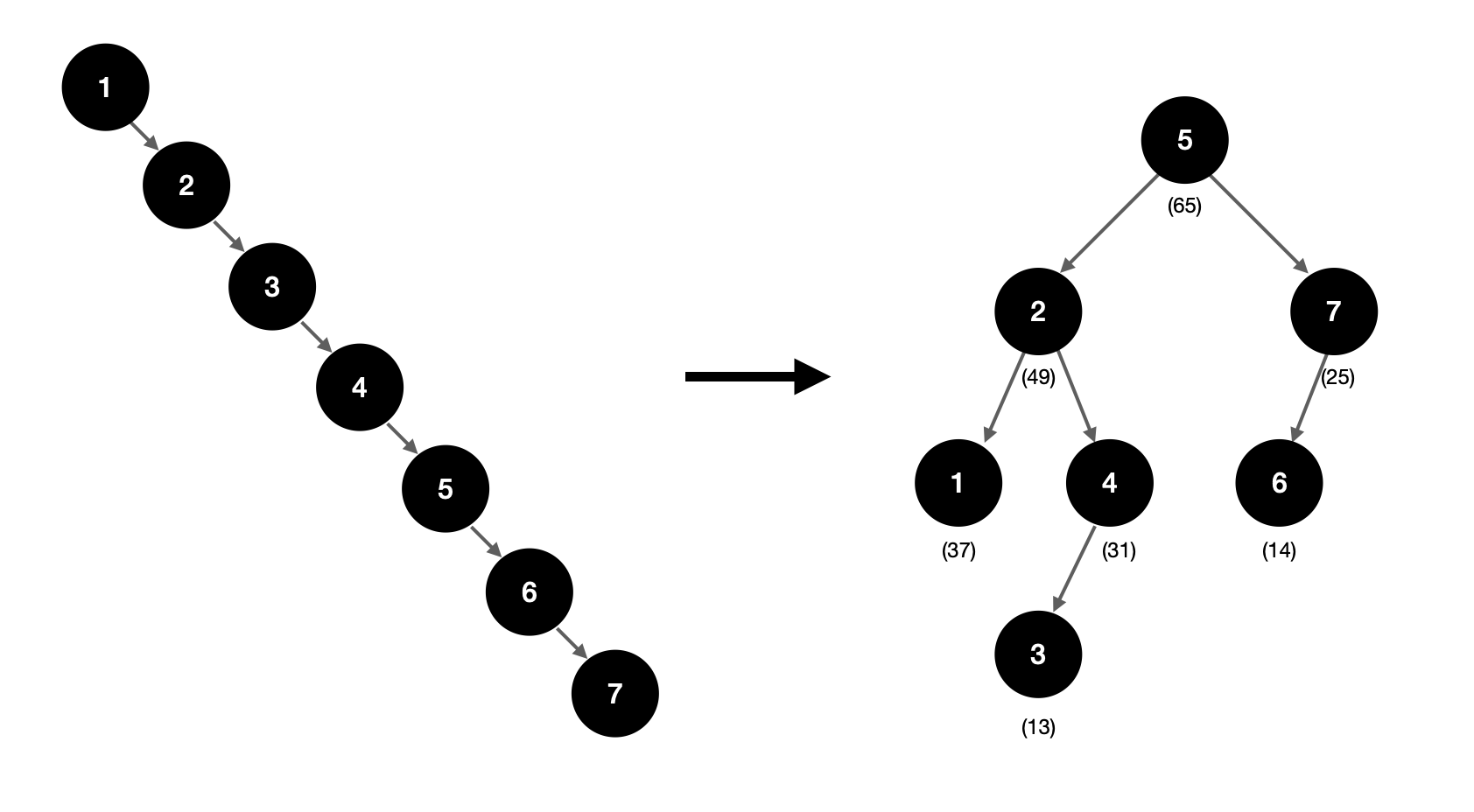
트립을 이해하는 또 다른 방법은 노드들을 우선순위가 높은 것부터 순서대로 추가한 이진 검색 트리라고 생각하는 것이다.
- 실제로 이진 검색 트리는 루트 부터 시작해서 아래로 자라나기 때문에, 부모 노드가 추가된 후에야 자식 노드가 있을 수 있다.
- 따라서 우선순위가 높을수록 위에 간다는 제약을 추가하면 결과적으로 우선순위 순서대로 추가한 이진 검색 트리가 된다.
트립의 높이
이와 같은 랜덤화가 의미가 있으려면 노드의 순서를 임의로 바꿨을 때 트리 높이의 기대치가 O(N)보다 작아야 한다. 그렇지 않으면 제약을 추가한 의미가 없다.
N개의 원소를 갖는 트립에서 어떤 원소 x를 찾으려 한다. 이때 방문해야 하는 노드 수의 기대치가 O(logN)임을 증명해보자.
- 이것을 증명하는 한 가지 방법은 트리를 한 단계 내려갈 때마다 후보가 되는 원소의 수가 선형으로 줄어드는 것이 아니라 지수적으로 줄어드는 점을 보이는 것이다.
트립의 루트는 N개의 노드 중 최대 우선순위를 가진다. 루트가 갖는 원소가 N개의 원소 중에서 r(r≥1)번째로 작은 원소라고 하자. 그러면 왼쪽 서브트리에는 r-1개, 오른쪽 서브트리에는 N-r개의 노드가 있을 것이다.
각 원소가 우리가 원하는 원소일 확률이 모두 동등하다고 가정하면,
- 우리가 찾는 원소가 왼쪽 서브트리에 있을 확률은 (r-1)/N,
- 루트에 있을 확률은 1/N,
- 오른쪽 서브트리에 있을 확률은 (N-r)/N 이 된다.
따라서 다음 단계에서 후보의 수의 기대치는 다음과 같다.
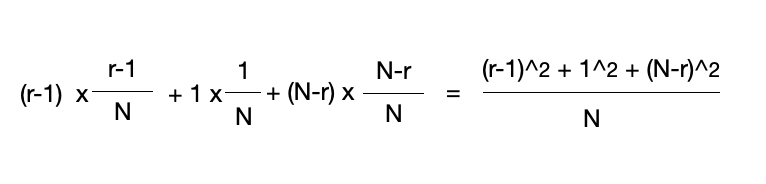
우선순위를 임의로 부여하기 때문에 모든 값은 루트가 될 가능성이 같다. 따라서 모든 r에 대한 값의 평균을 구해보면 대략 2N/3이 나오게 된다. 다시 말해 한 단계 내려갈 때마다 후보의 수가 평균적으로 2/3으로 줄어든다는 뜻이다. 따라서 O(logN) 단계를 거치면 답을 찾을 수 있음을 알 수 있다.
- 증명된 이유는 트리가 한 단계 내려갈 때마다 존재할 수 있는 노드의 수가 지수적으로 줄어들기 때문이다.
- 만약 N = 90이고 루트의 층이 1층이라면, 2층에서의 후보는 60가 되고 3층에서의 후보는 40 ... 로 줄어든다. 따라서 (2/3)^h*N으로 계속해서 줄어들게 된다.

트립 구현
필드에는 key, priority를 가진다. 노드가 생성될 때 랜덤함수로 우선순위를 부여한다. 또 하나 유의할 점은 자신을 루트로 하는 서브트리에 포함된 노드의 수를 저장하는 size 멤버이다.
- 이 값은 left, right가 바뀔 때마다 자동으로 갱신되며, 이 값을 이용하면 k번째 원소를 찾는 연산이나 X보다 작은 원소를 세는 연산등을 쉽게 구현할 수 있다.
class Node {
int data; // 이 노드에 저장된 원소
int priority; // 이 노드의 우선순위(proirity)
int size; // 이 노드를 루트로 하는 서브트리의 크기
Node left, right;
// data, left, right 초기화 및 난수 우선순위 생성
Node(int data) {
this.data = data;
this.priority = new Random().nextInt(100);
this.left = this.right = null;
}
void setLeft(Node left) {
this.left = left;
calcSize();
}
void setRight(Node right) {
this.right = right;
calcSize();
}
void calcSize() {
size = 1;
if (left != null) {
size += left.size;
}
if (right != null) {
size += right.size;
}
}
}
1. 노드 추가와 ‘쪼개기’ 연산
root를 루트로 하는 트립에 새 노드 node를 삽입해보자. 가장 먼저 확인해야 할 것은 root와 node의 우선순위다.
root 우선순위 > node 우선순위
만약 root의 우선순위가 더 높다면 node는 root 아래로 들어가야 한다.
- 왼쪽 서브트리로 가야 할지, 오른쪽 서브 트리로 가야 할지는 두 노드의 원소를 비교해서 정하면 된다. 그러고나서 재귀를 통해 삽입해주면 된다.
root 우선순위 < node 우선순위
문제가 되는 것은 node의 우선순위가 root보다 높은 경우이다. 이때는 node가 기존에 있던 루트 root를 밀어내고 이 트리의 포함되어 있던 노드들은 모두 node의 자손이 되어야만 한다. 이것을 구현하는 좋은 방법은 기존의 트리를 node가 가진 원소를 기준으로 ‘쪼개는’ 것이다.
- 이 트리를 쪼개서 기준보다 작은 원소만을 갖는 서브트리 하나, 큰 원소만을 갖는 서브트리로 두면 삽입 작업은 완료된다.
다행히 이 쪼개기 연산은 구현하기 그렇게 어렵지 않다. root를 루트로 하는 서브트리를 원소가 key보다 작은 노드들과 큰 노드들로 쪼개는 split(root, key)를 작성해보자.
- root의 원소가 key보다 작은 경우와 큰 경우로 나눠서 생각해보면 된다. 다행히 두 경우의 구현은 굉장히 비슷하다.
root 우선순위 < node 우선순위이면서, root의 원소가 더 작은 경우
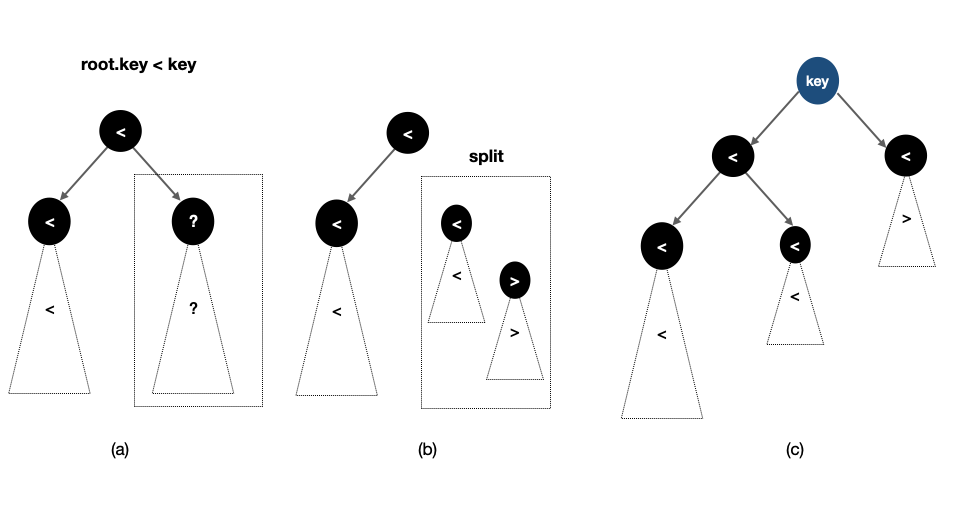
(a)는 root의 원소가 더 작은 경우 트리의 원소들과 key의 대소관계를 보여준다. root의 원소가 key보다 작기 때문에 그 왼쪽 서브트리의 원소들은 전부 key보다 작을 수밖에 없다. 따라서 key보다 큰 원소가 있을 수 있는 곳은 점선으로 표현된 오른쪽 서브트리 뿐이다.
- 따라서 재귀 호출을 적용해 (b)처럼 해당 트리를 key를 기준으로 쪼갠다.
- 쪼갠 결과 중 key보다 작은 원소를 갖는 트리를 root의 오른쪽 자손으로 연결한다.
- 그러면 key보다 작은 원소를 갖는 트리와 key보다 큰 원소를 갖는 트리가 남게되는데, 이 두 개의 트리가 각각의 key를 루트로 하는 왼쪽 서브트리와 오른쪽 서브트리가 되는 것이다.
public class Treap {
public Node insert(Node root, Node node){
if(root == null){
return node;
}
// node가 root를 대체헤야 한다. 해당 서브트리를 반으로 잘라 각각 자손으로 한다.
if(root.priority < node.priority){
Node[] splitted = split(root, node.key);
node.setLeft(splitted[0]);
node.setRight(splitted[1]);
return node;
}else if(root.key > node.key){
root.setLeft(insert(root.left, node));
}else {
root.setRight(insert(root.right, node));
}
return root;
}
// split 두 개의 트립으로 분리한다.
public Node[] split(Node root, int key) {
Node[] pair = new Node[2];
if (root == null) {
return pair;
}
// 루트가 key 미만이면 오른쪽 서브트리를 쪼갠다.
if (root.key < key) {
Node[] rs = split(root.right, key);
root.setRight(rs[0]);
return new Node[]{root, rs[1]};
} else { // root가 key 이상이면 왼쪽 서브트리를 쪼갠다.
Node[] ls = split(root.left, key);
root.setLeft(ls[1]);
return new Node[]{ls[0], root};
}
}
}
2. 노드 삭제와 ‘합치기’ 연산
기존 이진 검색 트리에서의 노드 삭제와 별반 다를 게 없다. 두 서브트리를 합칠 때 어느 쪽이 루트가 되어야 하는지를 우선순위를 통해 판단하는 점만 제외하면 거의 똑같다.
기존 이진 검색 트리에서의 삭제를 구현하는 방법은 여러가지 있지만, 그중 합치기 연산으로 구현하는 것이 간편하다. 노드 t를 지울 거라면, t의 두 서브트리를 합친 새로운 트리를 만든 뒤 이 트리를 t를 루트로 하는 서브트리와 바꿔치기한다.
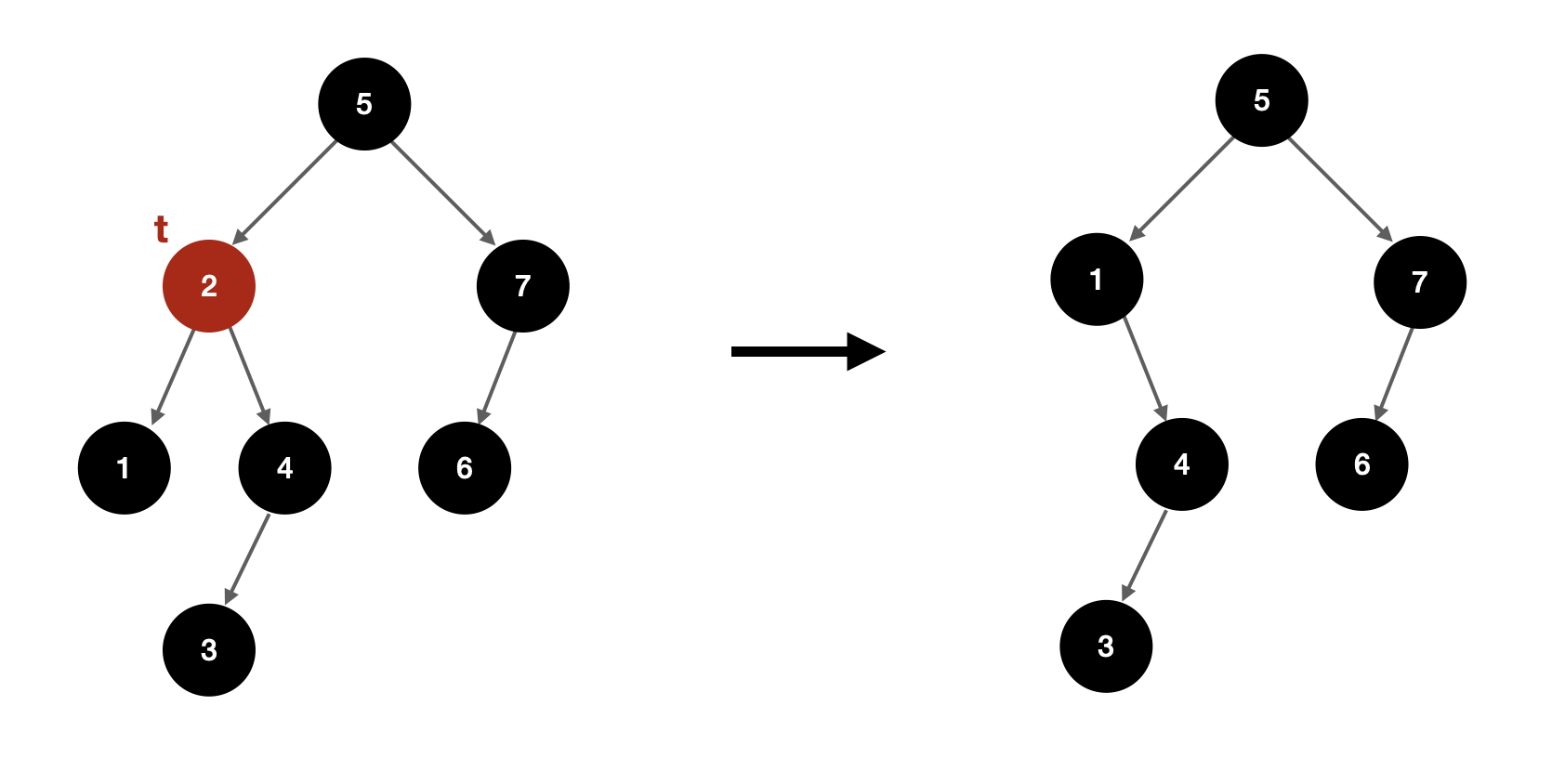
합치기 연산 구현은 어렵지 않다. 두 트리 A와 B를 합치려고 할 때, A의 최대 원소가 B의 최소 원소보다 작다고 하자. 원래 A와 B는 t의 왼쪽/ 오른쪽 서브트리였으므로 이 성질은 자연스레 성립한다.
다음은 기존 이진 검색 트리의 합치기 과정이다. 이제 A의 루트 a가 합쳐진 트리의 루트가 되도록 두 트리를 합쳐보자.
- 이때 a의 왼쪽 서브트리에 있는 원소들은 모두 a의 원소보다 작고, a의 오른쪽 서브트리와 B에 있는 원소들은 모두 a의 원소보다 크다.
- 따라서 오른쪽 서브트리와 B를 재귀적으로 합친 뒤 a의 오른쪽 자식으로 두면 합치기 연산은 완료된다.
트립의 루트는 우선순위로 결정되기 때문에, A의 최대 우선순위와 B의 최대 우선순위를 비교해줘야 한다.
- a의 우선순위가 b의 우선순위보다 더 크다면 a의 오른쪽 자식으로 a의 오른쪽 서브트리와 b를 합쳐서 붙인다. a.setRight(merge(a.right, b));
- 반대로 b의 우선순위가 더 크다면 b의 왼쪽 자식으로 a와 b의 왼쪽 자식을 합쳐서 붙인다. b.setLeft(merge(a, b.left));

// root를 루트로 하는 트립에서 key를 지우고 결과 트립의 루트를 반환한다.
public Node erase(Node root, int key){
if(root == null) return root;
// root를 지우고 양 서브트리를 합친 뒤 반환한다.
if(root.key == key){
Node ret = merge(root.left, root.right);
root = null;
return ret;
}
if(root.key > key){
root.setLeft(erase(root.left, key));
} else{
root.setRight(erase(root.right, key));
}
return root;
}
// a와 b가 두 개의 트립이고, max(a) < min(b)일 때 이 둘을 합친다.
private Node merge(Node a, Node b){
if(a == null) return b;
if(b == null) return a;
if(a.priority < b.priority){
b.setLeft(merge(a, b.left));
return b;
}
a.setRight(merge(a.right, b));
return a;
}
3. K번째 원소 찾기
위에서도 말했지만 BST를 직접 작성하는 경우는 표준 라이브러리의 구현에 원하는 기능이 없을 때 뿐이다. 그와 같은 기능 중 하나가 주어진 서브트리의 노드들을 포함한 원소의 크기 순으로 나열했을 때 k번째로 오는 노드를 찾는 연산이다. Node 클래스에서 서브트리의 크기 size를 계산해 저장해 두기 때문에 이것을 구현하기란 어렵지 않다.
root를 루트로 하는 서브트리는 왼쪽 자식 root → left를 루트로 하는 서브트리와 오른쪽 자식 root → right를 루트로 하는 서브트리 그리고 root 자신으로 구성되어 있다.
각 서브트리의 크기를 알고 있으면 k번째 노드가 어디에 속해 있을지 쉽게 알 수 있다. 왼쪽 서브트리의 크기를 l이라 할 때, 다음과 같이 세 가지의 경우로 나눌 수 있다.
- k ≤ l : k번째 노드는 왼쪽 서브트리에 속해 있다.
- k = l+1 : 루트가 k번째 노드이다.
- k > l+1 : k번째 노드는 오른쪽 서브트리에서 k-l-1번째 노드가 된다.
다음 구현을 보면 알겠지만 k번째 원소를 구하는 로직은 트립에 한정되어 있지 않다. 어느 BST에서나 적용이 될 수 있다.
// root를 루트로 하는 트리 중에서 k번째 원소를 반환한다.
public Node kth(Node root, int k) {
// 왼쪽 서브트리의 크기를 우선 계산한다.
int leftSize = 0;
if (root.left != null) {
leftSize = root.left.size;
}
if (k <= leftSize){
return kth(root.left, k);
}
if (k == leftSize + 1)
return root;
}
return kth(root.right, k - leftSize - 1);
}
4. X보다 작은 원소 세기
또 다른 유용한 연산으로 특정 범위 [a, b)가 주어질 때 이 범위 안에 들어가는 원소들의 숫자를 계산하는 연산이 있다. 이 연산은 주어진 원소 X보다 작은 원소의 수를 반환하는 countLessThan(x)가 있으면 간단하게 구현할 수 있다.
- [a, b) 범위 안에 들어가는 원소들의 수는 countLessThan(b) - countLessThan(a)로 표현할 수 있기 때문이다.
countLessThan(x)는 탐색 함수를 변형해 간단하게 만들 수 있다.
- 먼저 root의 원소가 x보다 큰지 비교한다.
- 만약 root의 원소가 x보다 같거나 크면 root와 오른쪽 서브트리에 있는 원소들은 모두 x이상이므로, 왼쪽 서브트리에 있는 원소들만 재귀적으로 세서 반환하면 된다.
- 만약 root의 원소가 x보다 작다면,
- 그 왼쪽 서브트리에 있는 원소들을 모두 x보다 작으므로 재귀적으로 세지 않아도 전부 답에 들어간다는 것을 알 수 있다.
- 오른쪽 서브트리에서 x보다 작은 원소를 재귀적으로 찾고 이것에 왼쪽 서브트리에 포함돈 노드 및 루트의 개수를 더해주면 된다.
이 구현 또한 트립에 한정되어 있지 않고 BST이기만 하면 잘 동작한다.
// X보다 작은 키를 갖는 노드의 수를 반환한다.
public int countLessThan(Node root, int x) {
if (root == null) {
return 0;
}
if (root.key >= x) {
return countLessThan(root.left, x);
}
// x가 현재 노드보다 클 경우
// 왼쪽 서브트리 크기 + 현재 노드 + 오른쪽에서 x보다 작은 노드 수
int ls = root.left == null ? 0 : root.left.size;
return ls + 1 + countLessThan(root.right, x);
}
💡 트립(Treap) 전체 구현 코드는 github에서 확인할 수 있습니다.
'Dot Algo∙ DS > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘] 접미사 배열(Suffix Array)와 LCP 배열(Lognest Common Prefix Array) (Java) (0) | 2022.04.07 |
|---|---|
| [알고리즘] 펜윅 트리(Fenwick Tree) 빠르고 간단한 구간 합 구하기 (Java) (0) | 2022.01.03 |
| [알고리즘] 이분 매칭 (Bipartite Matching) 알고리즘 (Java) (0) | 2022.01.01 |
| [알고리즘] 네트워크 유량, 포드-폴커슨(Ford-Fulkerson) 알고리즘 (Java) (0) | 2021.12.27 |
| [알고리즘] SCC(Strongly Connected Component) (백준 2150번 풀이) (0) | 2021.12.05 |




