서로소 집합(Disjoint Sets)이란?
서로소 집합(Disjoint Sets)은 공통원소가 없는 두 집합을 뜻한다.

서로소 집합 자료구조 (Union-find)
서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조로, 합치기 찾기(Union-find) 자료구조라고도 불린다.
서로소 집합 자료구조는 두 종류의 연산을 지원한다.
- Union(합집합) : 두개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산
- Find(찾기) : 특정한 원소가 속한 집합이 어떤 집합인지 알려주는 연산
동작 과정
서로소 집합 자료구조에서는 연결성을 통해 손쉽게 집합의 형태를 확인할 수 있다.
- 합치기(Union) 연산을 확인하여, 서로 연결된 두 노드 A,B를 확인한다.
- A와 B의 루트 노드 A', B'를 각각 찾는다.
- A'를 B'의 부모 노드로 설정한다.
- 모든 합집합(Union) 연산을 처리할 때까지 1번의 과정을 반복한다.
예시) Union(1,4), Union(2,3), Union(2,4), Union(5,6)

문제점
기본적인 형태의 서로소 집합 자료구조에서는 루트 노드에 즉시 접근할 수 있다. (순차탐색 -> 탐색 효율 낮음)
그래서 Union 연산이 편향되게 이루어지는 경우 Find 연산이 비효율적으로 동작할 수 있다.
해결방안
Find 연산을 최적화하기 위한 방법으로 경로 압축(Path Compression)을 이용할 수 있다.
- parent[n] = find(parent[n]); Find 함수를 재귀적으로 호출한 뒤에 부모 테이블 값을 바로 갱신한다.
static int parent(int x){
if(parent[x] != x){
parent[n] = find(parent[n]);
}
return parent[n];
}
Union-Find 코드
public class tt {
private static int n;
private static int[] parents;
public static void main(String[] args) {
n = 10;
parents = new int[n + 1]; // 값 초기화 및 노드 연결 전
int[][] graph = {{1,2},{2,3},{3,4},{5,6},{6,7},{7,8},{9,10}};
System.out.println("< 연결 전 >");
for (int i = 1; i <= n; i++) {
parents[i] = i;
System.out.print(parents[i] + " ");
}
System.out.println();
//노드 연결
for(int i=0; i<graph.length; i++) {
int a = graph[i][0];
int b = graph[i][1];
union(a,b);
}
//연결 후
System.out.println("< 연결 후 >");
for (int i = 1; i <= n; i++) {
System.out.print(parents[i] + " ");
}
System.out.println();
}
static int find(int[] parents, int x) {
if (parents[x] == x) {
return x;
}
int parent = find(parents, parents[x]);
return parent;
}
static void union(int[] parents, int x, int y) {
x = find(parents, x);
y = find(parents, y);
// 더 find 값으로 부모 노드 설정
if (x < y) {
parents[y] = x;
}
else {
parents[x] = y;
}
}
}
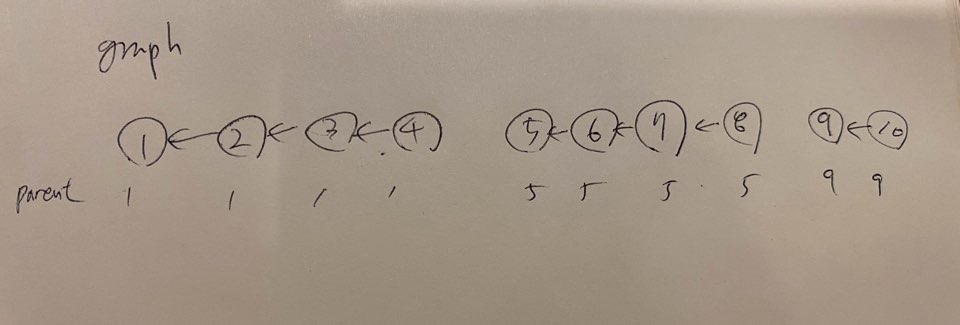
실행결과

Union-Find로 사이클 판별하기 (무방향그래프)
서로소 집합은 무방향 그래프 내에서의 사이클을 판별할 때 사용할 수 있다.
- 방향 그래프의 사이클 여부는 DFS를 이용하여 판별할 수 있다.
사이클 판별 알고리즘 과정
- 각 간선을 하나씩 확인하며 두 노드의 루트 노드를 확인한다.
- 루트 노드가 서로 다르다면 두 노드에 대하여 Union 연산을 수행한다.
- 루트 노드가 서로 같다면 사이클(Cycle)이 발생한 것이다.
- 그래프에 포함되어 있는 모든 간선에 대하여 1번 과정을 반복한다.
public class tt {
private static int n;
private static int[] parents;
public static void main(String[] args) {
n = 10;
parents = new int[n + 1]; // 값 초기화 및 노드 연결 전
int[][] graph = {{1,2},{2,3},{3,4},{1,4}};
System.out.println("< 연결 전 >");
for (int i = 1; i <= n; i++) {
parents[i] = i;
System.out.print(parents[i] + " ");
}
System.out.println();
//노드 연결 // 사이클 판별하기
for(int i=0; i<graph.length; i++) {
int a = graph[i][0];
int b = graph[i][1];
if(isCycle(a,b)) {
System.out.println("cycle!");
break;
}else {
union(a,b);
}
}
//연결 후
System.out.println("< 연결 후 >");
for (int i = 1; i <= n; i++) {
System.out.print(parents[i] + " ");
}
System.out.println();
}
static int find(int x) {
if (parents[x] == x) {
return x;
}
int parent = find(parents[x]);
return parent;
}
static void union(int x, int y) {
x = find(x);
y = find(y);
// 더 find 값으로 부모 노드 설정
if (x < y) {
parents[y] = x;
}
else {
parents[x] = y;
}
}
static boolean isCycle(int x, int y) {
boolean result = false;
if (parents[x] == parents[y]) result = true;
return result;
}
}

실행결과

'Dot Algo∙ DS > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘/ 그래프] 위상 정렬 (topology Sort) (Java) (0) | 2021.04.23 |
|---|---|
| [알고리즘/ 그래프] 최소 스패닝 트리 - 크루스칼(Kruskal)과 프림(Prim) 알고리즘 (Java) (0) | 2021.04.22 |
| [알고리즘/ 그래프] DFS와 BFS 정리 (Java) (0) | 2021.03.22 |
| [알고리즘] 동적계획법 DP (Dynamic Programming) 정리 (Java) (7) | 2021.03.09 |
| [알고리즘/ 그래프] 다익스트라(Dijkstra) vs 플로이드 와샬(Floyd Warshall) (JAVA) (0) | 2021.03.05 |




