다익스트라(Dijkstra) vs 플로이드 와샬(Floyd Warshall)
- Dijkstra 알고리즘은 하나의 정점에서 출발했을 때 다른 모든 정점으로의 최단 경로를 구하는 알고리즘이다.
- 그에 반해 Floyd Warshall 알고리즘은 모든 정점에서 다른 모든 정점으로의 최단 경로를 구하는 알고리즘이다.
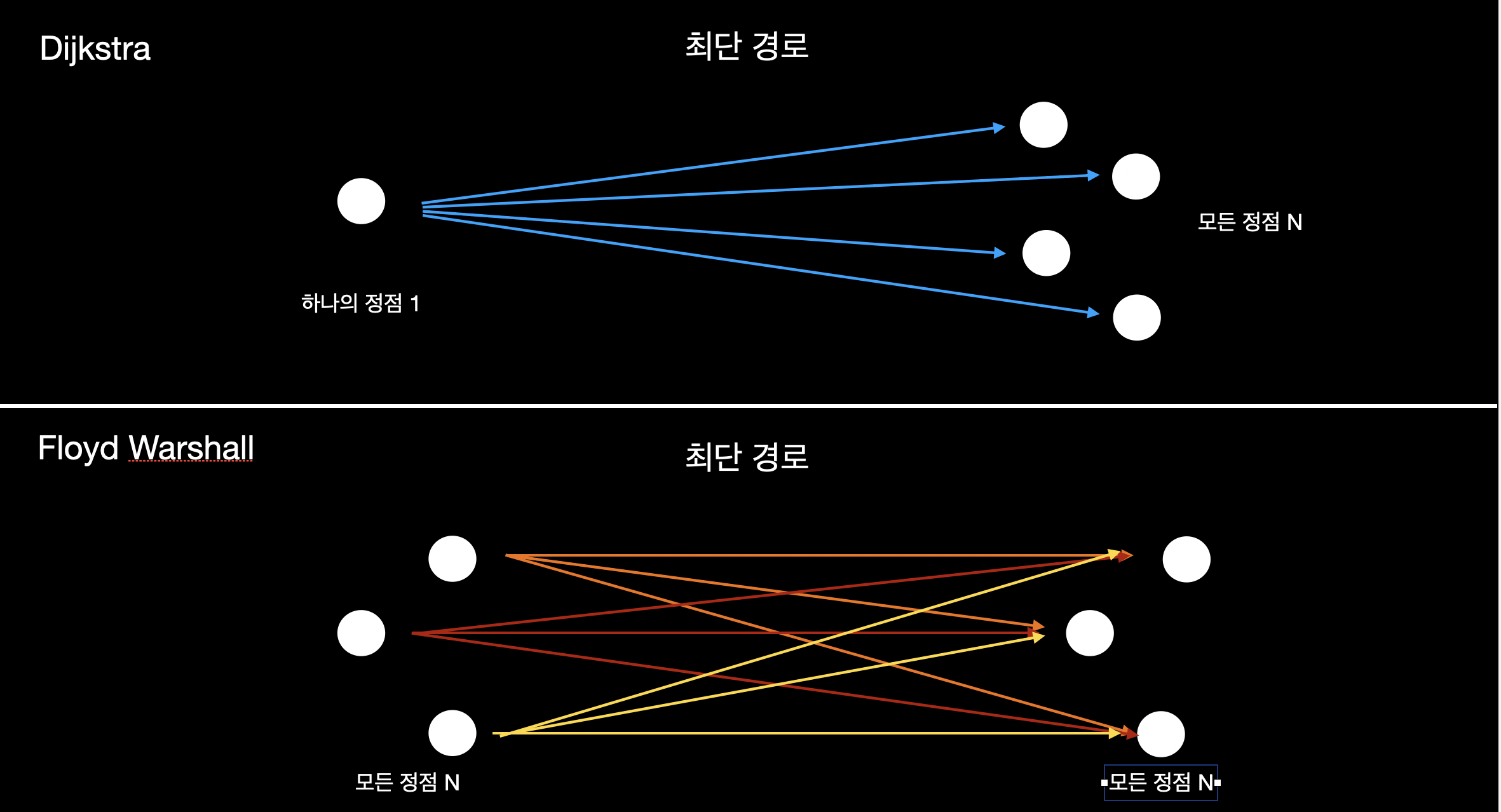
- Dijkstra 알고리즘은 매번 가장 적은 비용을 가진 노드를 하나씩 꺼낸 다음 그 노드를 거쳐가는 비용, 즉 가장 적은 비용을 하나씩 선택하는 로직으로 구성되었다면,
- Floyd Warshall 알고리즘의 핵심 아이디어는 애초에 거쳐가는 정점을 하나씩 다 설정을 하여 직접 확인하는 방법, 즉 거쳐가는 정점을 기준으로 최단 거리를 구하도록 구성되어있다.

다익스트라(Dijkstra) 알고리즘
다익스트라의 최단 경로 알고리즘은 가장 유명한 그래프 알고리즘 중 하나이다. 단일 시작점 최단 경로 알고리즘으로, 시작 정점 s에서부터 다른 정점들 까지의 최단 거리를 계산한다.
- DP를 활용한 최단경로 탐색 알고리즘으로 흔히 인공위성 GPS 소프트웨어에서 가장 많이 사용된다.
아래와 같은 그래프가 존재할 때 Dijkstra 알고리즘을 통해 하나의 정점에서 다른 모든 정점의 최단 경로를 구해보자.

실제로 코드에 사용하는 것은 1차원 배열이지만 컴퓨터 안에서 처리할 때는 이차원 배열 형태로 처리해야 한다. 아래의 표는 특정 노드에서 다른 노드로가는 그래프이다.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0 | 2 | 5 | 1 | inf | inf |
| 2 | 2 | 0 | 3 | 2 | inf | inf |
| 3 | 5 | 3 | 0 | 3 | 1 | 5 |
| 4 | 1 | 2 | 3 | 0 | 1 | inf |
| 5 | inf | inf | 5 | 1 | 0 | 2 |
| 6 | inf | inf | 5 | inf | 2 | 0 |
1번 노드를 기준으로 잡고 최단 경로를 구해보자.
해당 노드에 직접적으로 연결된 노드는 2, 3, 4번 노드로 이 중에서 가장 적은 비용이 드는 노드는 4번 노드(값 : 1)이다.
| 0 | 2 | 5 | 1 | inf | inf |
근데 위의 그래프를 보면 5로 가는 최소비용은 inf이지만 4를 거쳐 5로 가는 비용은 2이므로 최소 비용을 갱신해준다.
또한 4를 거쳐서 3으로 가는 경우 비용이 4이므로 기존보다 작기 때문에 이 또한 갱신해준다
| 0 | 2 | 4 | 1 | 2 | inf |
이제 4번 다음으로 비용이 적은 노드는 2번 노드이다.
하지만 2번 노드를 통해서는 갱신되는 경우가 없기 때문에 배열은 그대로 유지한다
2번 노드 다음에는 5번 노드(값 : 2)의 비용이 가장 적다.
5번을 거쳐서 가는 경우에 3번 비용이 3, 6으로 가는비용은 4가 되므로 최단 경로의 값을 갱신해준다.
| 0 | 2 | 3 | 1 | 2 | 4 |
이러한 방식으로 3번, 6번 노드를 방문하여 계산을 하면 최종적으로 아래와 같은 배열이 완성된다
| 0 | 2 | 3 | 1 | 2 | 4 |
우선순위 큐를 사용하는 다익스트라(Dijkstra) 알고리즘
다익스트라 알고리즘은 너비 우선 탐색과 유사한 형태를 가진 알고리즘으로, 너비 우선 탐색처럼 시작점에서 가까운 순서대로 정점을 방문해간다. 물론 가중치가 있는 그래프에서는 너비 우선 탐색을 그대로 적용할 순 없기 때문에 우선순위 큐를 사용하여 이를 해결한다.
- 다익스트라 알고리즘은 우선순위 큐 + BFS의 형태를 가지고 있다.
- 각 정점까지의 최단 거리를 저장하는 배열 dp[]를 유지하며, 정점을 방문할 때마다 인접한 정점을 모두 검사한다.
- 간선 (u, v)를 검사한다고하면 u까지의 최단 거리에 (u, v)의 가중치를 더해 v까지의 경로의 길이를 찾는다. 만약 이 길이가 최단거리라면 dp[v]를 갱신하고, (v, dp[v])를 큐에 넣는다.
public class DijkstraExample {
static List<Node>[] list;
static int[] dp;
static boolean[] check;
public static void main(String[] args) {
int[][] a = {{1,2,2}, {1,4,1}, {1,3,5}, {2,3,3}, {2,4,2},
{3,4,3}, {3,5,1}, {4,5,1}, {5,6,2}, {3,6,5}};
int n =6;
solution(n,a);
}
// Dijkstra 배열 초기화
static void solution(int n , int maps[][]) {
check = new boolean[n+1];
dp = new int[n+1];
list = new ArrayList[n+1];
for(int i=1; i<n+1; i++ ) {
list[i] = new ArrayList<>();
}
for(int i=0; i<maps.length; i++) {
int a = maps[i][0];
int b = maps[i][1];
int c = maps[i][2];
list[a].add(new Node(b,c));
list[b].add(new Node(a,c));
}
dijkstra(1);
for(int num : dp) {
System.out.print(num +" ");
}
}
// Dijktstra 알고리즘 (우선순위 큐(Heap)을 이용한 알고리즘)
static void dijkstra(int start) {
Queue<Node> q = new PriorityQueue<>();
Arrays.fill(dp, Integer.MAX_VALUE);
q.add(new Node(start,0));
dp[start] = 0;
while(!q.isEmpty()) {
Node node = q.poll();
int to = node.to;
if(check[to]) continue;
else check[to] = true;
for(Node nxt : list[to]) {
if(dp[nxt.to] >= dp[to] + nxt.weight) {
dp[nxt.to] = dp[to] + nxt.weight;
q.add(new Node(nxt.to, dp[nxt.to]));
}
}
}
}
}
class Node implements Comparable<Node>{
int to;
int weight;
Node(int to, int weight){
this.to = to;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
return Integer.compare(this.weight, o.weight);
}
}
플로이드 와샬(Floyd Warshall) 알고리즘
다익스트라나 벨만포드는 한 시작점에서 다른 모든 정점까지의 거리를 구해준다. 모든 쌍 간의 최단 거리를 구하고 싶다면 플로이드 와샬 알고리즘을 사용하면 된다.
경유점
플로이드 알고리즘은 경로의 경유점 개념을 알아야한다. 두 정점 u, v를 잇는 어떤 경로가 있다고 할때 이 경로는 시작점 u와 끝점 v를 가지는 것이다. 이 외에 이 경로는 다른 정점들을 지나쳐 갈 수 도 있다.
- u와 v를 직접 연결하는 간선이 없거나, 다른 정점을 경유해서 가는 편이 전체 경로가 더 짧아지기 때문이다. 이와 같이 경로가 거쳐가는 정점들을 경유점이라 한다.
아래와 같은 그래프가 존재할 때 플로이드 와샬 알고리즘을 통해 모든 정점들의 최단 경로를 구해보자.

각각의 정점이 다른 정점으로 가는 비용을 이차원 배열로 출력하면 다음과 같다.
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 5 | inf | 8 |
| 2 | 7 | 0 | 9 | inf |
| 3 | 2 | inf | 0 | 4 |
| 4 | inf | inf | 3 | 0 |
이제 각각의 노드를 차례대로 기준으로 잡고 최단 경로를 구하면 된다
1) 노드 1을 거쳐가는 경우
1을 거쳐서 가는 경우가 더 빠르다면 그 경우로 최단 경로의 길이를 갱신해주는 것으로 파란색으로 된 6곳만 갱신이 되었다
X에서 Y로 가는 최소 비용 VS X에서 노드 1로 가는 비용 + 노드 1에서 Y로 가는 비용
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 5 | inf | 8 |
| 2 | 7 | 0 | 9 | 15 |
| 3 | 2 | 7 | 0 | 4 |
| 4 | inf | inf | 3 | 0 |
2) 노드 2을 거쳐가는 경우
노드 1과 마찬가지로 계산을 해주면 된다
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 5 | 14 | 8 |
| 2 | 7 | 0 | 9 | 15 |
| 3 | 2 | 7 | 0 | 4 |
| 4 | inf | inf | 3 | 0 |
위와 같은 방식으로 노드3, 노드4도 수행해주면 최종적으로 아래와 같은 결과가 나오게 된다
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 5 | 11 | 8 |
| 2 | 7 | 0 | 9 | 13 |
| 3 | 2 | 7 | 0 | 4 |
| 4 | 5 | 10 | 3 | 0 |
플로이드 와샬(Floyd Warshall) 알고리즘 코드
위의 과정들을 보면 경유점을 지나는 최단 거리는 다음과 같이 구할 수 있다. C(u, v)는 0번 정점부터 k번 정점까지만을 경유점으로 썼을 때 u에서 v까지 가는 최단 경로의 길이가 된다.
- Ck(u, v) = Math.min( (Ck-1(u, k)+Ck-1(k, v)), Ck-1(u,v) )
이 점화식에서 Ck의 모든 값은 Ck-1에만 의존하기 때문에 반복 DP로 쉽게 풀 수 있다. 이렇게 구현한 플로이드 와샬 알고리즘은 3중 for문을 사용하기 때문에 O(V^3)이 된다.
public class FloydWarshall {
public static void main(String[] args) {
int[][] a = {{1,2,5}, {2,1,7},{3,1,2},{1,4,8},{2,3,9},
{3,4,3}, {4,3,3}};
int n =4;
solution(n,a);
}
static void solution(int n, int[][] arr) {
int[][] floyd = new int[n][n];
// 결과 그래프 초기화
for(int i=0; i<n; i++) {
for(int j=0; j<n; j++){
if(i==j) {
floyd[i][j] =0;
}else floyd[i][j] = 1_000_000_000;
}
}
// 결과 그래프 입력
for(int i=0; i<arr.length; i++) {
floyd[arr[i][0]-1][arr[i][1]-1] = arr[i][2];
}
// k : 거쳐가는 노드 (기준)
for(int k=0; k<n; k++) {
// i : 출발 노드
for(int i=0; i<n; i++) {
// j : 도착 노드
for(int j=0; j<n; j++) {
// i에서 j로 가는 최소 비용 VS
// i에서 노드 k로 가는 비용 + 노드 k에서 jY로 가는 비용
if(floyd[i][k] + floyd[k][j] < floyd[i][j]) {
floyd[i][j] = floyd[i][k] + floyd[k][j];
}
}
}
}
for(int i=0; i<n; i++) {
for(int j=0; j<n; j++) {
System.out.print(floyd[i][j]+ " ");
}
System.out.println();
}
}
}
다익스트라(Dijkstra) vs 플로이드 와샬(Floyd Warshall) 총 정리
| 다익스트라(Dijkstra) | 플로이드 와샬(Floyd Warshall) | |
| 용도 | 한 정점 → 다른 모든 정점 최단 거리를 구할 때 | 모든 정점 → 모든 정점 최단 거리를 구할 때 |
| 공간복잡도 | 인접행렬 O(V^2) 인접리스트 O(V+E) - 사용 권장 |
이차원배열 O(V^2) |
| 시간 복잡도 | 인접행렬 O(V^2) 인접리스트 + 우선순위 큐 O((V+E)logV) |
3중 포문 O(V^3) |
플로이드 와샬 알고리즘은 시간 복잡도가 매우 높기 때문에 효율적인 코드 작성이 필요할 때(코테)는 V의 크기가 크다(500 이상)면 가급적 피하는 것이 좋다. 그 대신 다익스트라나 다른 방법을 이용해서 더 효율적인 코드를 작성해야 한다.
❐ V의 크기가 큰 모든 정점 최단 경로 찾기 예제 (플로이드 -> 다익스트라)
그래도 플로이드 와샬 입장에서도 변론을 하자면 V의 범위가 적당하다면 모든 정점의 최단 경로를 구할 때는 플로이드 와샬 알고리즘이 최고다.
'Dot Algo∙ DS > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘/ 그래프] 위상 정렬 (topology Sort) (Java) (0) | 2021.04.23 |
|---|---|
| [알고리즘/ 그래프] 최소 스패닝 트리 - 크루스칼(Kruskal)과 프림(Prim) 알고리즘 (Java) (0) | 2021.04.22 |
| [알고리즘/ 그래프] 서로소 집합 자료구조 Union-find (Java) (0) | 2021.04.21 |
| [알고리즘/ 그래프] DFS와 BFS 정리 (Java) (0) | 2021.03.22 |
| [알고리즘] 동적계획법 DP (Dynamic Programming) 정리 (Java) (7) | 2021.03.09 |




