#9663 N-Queen
난이도 : 골드 5
유형 : DP / 백트래킹
9663번: N-Queen
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다. N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
www.acmicpc.net
▸ 문제
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.
N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
▸ 입력
첫째 줄에 N이 주어진다. (1 ≤ N < 15)
▸ 출력
첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.
문제 풀이
백트래킹의 대표문제이다. DFS를 통해 모든 경우를 탐색하되 백트래킹을 사용하여 서로 공격할 수 없는 위치에만 놓으면 된다.
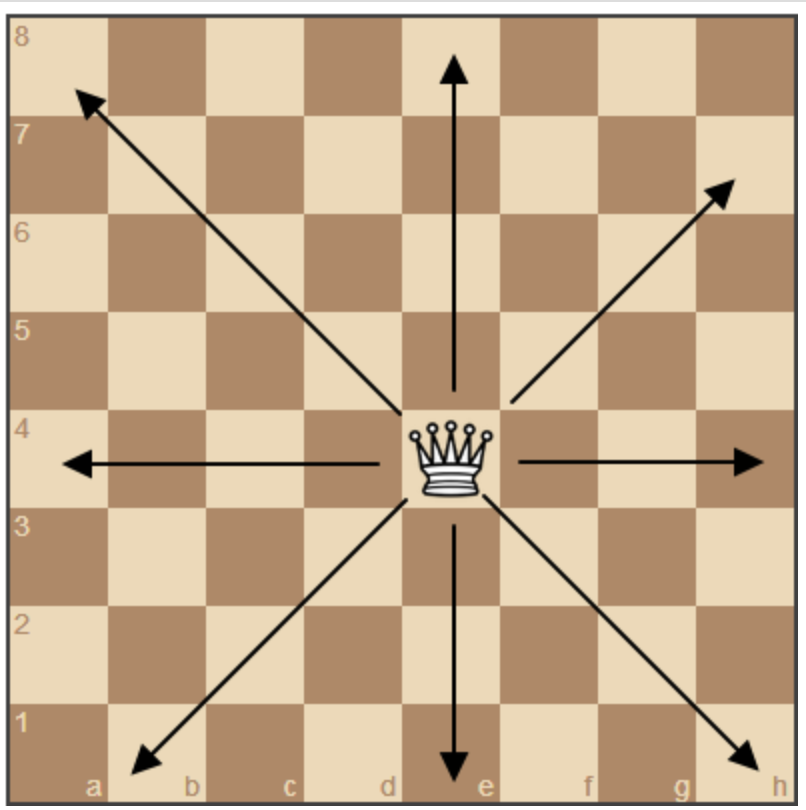
퀸의 움직임은 가로방향, 세로방향, 대각선 방향(오른쪽, 왼쪽) 총 4가지이다.
아래에 있는 방향은 아직 미지수이고, 가로 방향은 dfs를 열을 기준으로 탐색하면 되어서 따로 조건으로 넣지 않아도 된다.
그래서 조건을 따질 때 아래의 두가지를 체크해주면 된다.
1) 세로방향에 이미 퀸이 놓여져있는지
2) \ 또는 / 방향으로 나보다 낮은 열에 이미 퀸이 놓여져있는지
NxN 체스판이라고 할 때, 전체적인 흐름을 보면 다음과 같다.
행 : x, 열 : depth 이라고 하자. >> map[depth][x]
1) 1열에서 행의 모든 start 경우로 다 탐색을 시작
> (1,1) (1,2) (1,3) .... (1,n-1)
2) 2열부터 DFS 탐색 시작 dfs(map,2);
2-1) 1)과 마찬가지로 2열에서 모든 행의 경우를 탐색
3) 여기서 노드 유망성 체크 (단, 서로 공격할 수 없는 위치에 있는 경우만 허용한다.)
3-1) 노드 유망성이 허용되면(퀸 공격x) 그대로 탐색
3-2) 현재 놓여져 있는 퀸으로 부터 공격을 받으면 탐색 종료 후 그 부모노드로 되돌아감 - ✂️백트래킹(가지치기)
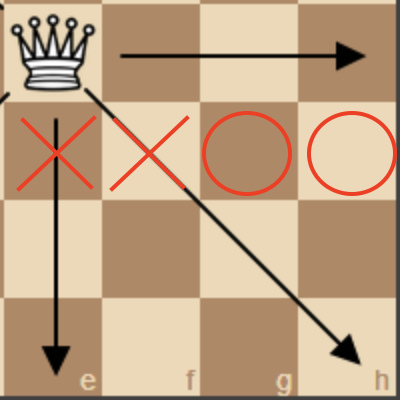
만약 퀸이 1행 1열에 놓여있다면, 다음 2열 탐색에서 (1행 2열), (2행 2열)에는 퀸의 위치가 올 수 없다
노드 유망성 체크 코드
static boolean condition(int[][] map, int x, int depth) {
// 세로 방향
for(int i=1; i<depth; i++) {
if(map[i][x] == 1) return false;
}
// \방향
int px = x - 1;
int py = depth - 1;
while(px > 0 && py > 0) {
if(map[py--][px--] == 1)
return false;
}
// /방향
px = x+1;
py = depth-1;
while(px < n+1 && py > 0) {
if(map[py--][px++] == 1)
return false;
}
return true;
}
풀이 코드
import java.io.*;
public class Main {
static int n;
static int[][] map;
static int count=0;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
for(int i=1; i<n+1; i++) {
map = new int[n+1][n+1];
map[1][i] =1;
dfs(map, 2);
}
System.out.println(count);
}
static void dfs(int[][] map, int depth) {
if(depth == n+1) {
count++;
System.out.println("coin!");
return;
}
for(int i=1; i<n+1; i++) {
if(condition(map, i, depth)) {
map[depth][i] = 1;
dfs(map, depth+1);
map[depth][i] = 0;
}
}
}
static boolean condition(int[][] map, int x, int depth) {
// 세로 방향
for(int i=1; i<depth; i++) {
if(map[i][x] == 1) return false;
}
// \방향
int px = x - 1;
int py = depth - 1;
while(px > 0 && py > 0) {
if(map[py--][px--] == 1)
return false;
}
// /방향
px = x+1;
py = depth-1;
while(px < n+1 && py > 0) {
if(map[py--][px++] == 1)
return false;
}
return true;
}
}
2차 풀이 코드
이제 위의 코드에서 좀 더 멋있고 효율성있게 코드하고 싶다하면 아래와 같이 하면된다.
2차원 배열을 1차원 배열로 바꾸면 메모리 공간과 조건을 따질 때 연산 시간이 줄어들어 효율성이 더 좋아진다.
2차원 배열은 map[depth][x] = 1 로 퀸의 여부를 체크했다면,
1차원 배열에서는 map[depth] = x 로 퀸의 여부를 체크한다.
그래서 예로, map[1] =1 은 (1,1)에 퀸이 있다는 뜻이다.
이게 가능한 이유는 애초에 한 열(depth)에 퀸이 하나만 올 수 있기 때문이다.
* 위의 경우 (1,2) (1,3) .. (1,n-1) 에는 올 수 없음
import java.io.*;
public class Main {
static int n;
static int[] map;
static int count=0;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
for(int i=1; i<n+1; i++) {
map = new int[n+1];
map[1] = i; // (1,i)에 queen
dfs(2);
}
System.out.println(count);
}
static void dfs(int depth) {
if(depth > n) {
count++;
}
else {
for(int i=1; i<n+1; i++) {
map[depth] = i; // (depth,i)에 queen
if(check(depth)) {
dfs(depth+1);
}
// 없어도 됨. 이미 map[depth] = i에서 부모 퀸의 위치가 초기화 되었기 때문이다.
// map[depth] = 0;
}
}
}
static boolean check(int depth) {
for(int i=1; i<depth; i++) {
// 열이 같으면 false
if(map[i] == map[depth]) return false;
// 00 01 02 03
// 10 11 12 13
// 20 21 22 23
// 30 31 32 33
// (/\) 양방향 대각선
if(Math.abs(i-depth) == Math.abs(map[i]-map[depth])) return false;
}
return true;
}
}
'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 2573번 빙산 (Java) (0) | 2021.05.16 |
|---|---|
| [BOJ] 백준 1261번 알고스팟 (Java) (0) | 2021.05.15 |
| [BOJ] 백준 16234번 인구 이동 (Java) (0) | 2021.05.12 |
| [BOJ] 백준 16916번 부분 문자열 KMP (Java) (0) | 2021.05.11 |
| [BOJ] 백준 1389번 케빈 베이컨의 6단계 법칙 (Java) (0) | 2021.05.09 |




