#7453 합이 0인 네 정수
난이도 : 골드 2
유형 : 이진탐색/ 투 포인터
7453번: 합이 0인 네 정수
첫째 줄에 배열의 크기 n (1 ≤ n ≤ 4000)이 주어진다. 다음 n개 줄에는 A, B, C, D에 포함되는 정수가 공백으로 구분되어져서 주어진다. 배열에 들어있는 정수의 절댓값은 최대 228이다.
www.acmicpc.net
▸ 문제
정수로 이루어진 크기가 같은 배열 A, B, C, D가 있다.
A[a], B[b], C[c], D[d]의 합이 0인 (a, b, c, d) 쌍의 개수를 구하는 프로그램을 작성하시오.
▸ 입력
첫째 줄에 배열의 크기 n (1 ≤ n ≤ 4000)이 주어진다. 다음 n개 줄에는 A, B, C, D에 포함되는 정수가 공백으로 구분되어져서 주어진다. 배열에 들어있는 정수의 절댓값은 최대 228이다.
▸ 출력
합이 0이 되는 쌍의 개수를 출력한다.
문제 풀이
최대 4000개의 원소를 가지므로 브루트포스하게 모든 경우의 수를 조사하면 4000^4 = 256,000,000,000,000번의 연산이 진행된다. 딱봐도 시간초과가 발생할 정도의 연산크기이다. 그래서 연산을 나눠줘야 하는데 이는 A,B 그리고 C,D를 각 하나의 집합으로 합친 다음에 생성된 두개의 집합 AB와 CD를 선형 시간복잡도보다 더 낮은 방법으로 탐색을 해주면 된다.

AB[]와 CD[]의 두 배열의 값을 비교하면서 0이되는 값을 찾아주는 로직을 설계하면 되는데 여기서 투 포인터와 이진탐색 기법을 사용하여 선형시간보다 더 빠르게 탐색해주면 된다.
시뮬레이션
기존 이진탐색처럼 크기를 반으로 갈라치는 기법은 아니지만 각 정렬된 배열에 투 포인터를 사용하여 빠르게 합이 0이 되는 값을 탐색할 수 있는 방법을 사용하여 선형탐색시간보다 더 빠르게 동작하는 모습을 확인할 수 있다.
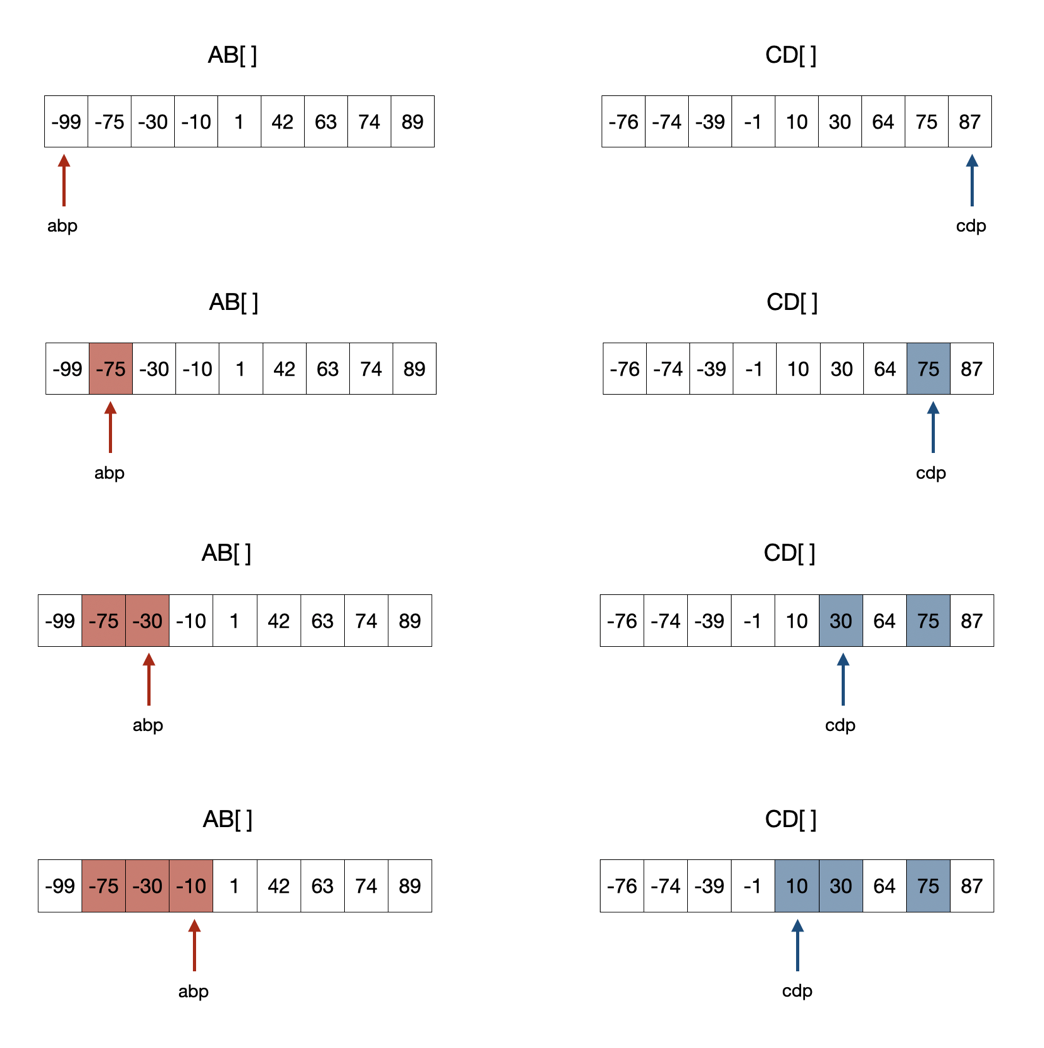

설계
- a,b,c,d를 ab, cd배열로 압축시킨다.
- ab와 cd배열을 정렬한 후 이진탐색을 통해 합이 0이 되는 지점을 탐색한다.
- abv+cdv <0, 값을 올려야 하므로 ab포인터가 한 칸 앞으로 이동한다. abp+=1;
- abv+cdv >0, 값을 내려야 하므로 cd포인터가 한 칸 뒤로 이동한다. cdp-=1;
- abv+cdv=0, 0이 되는 구간이므로 중복되는 원소가 있는지 확인한 후 카운트를 해준다.
- ab포인터가 n*n이 되거나 cd포인터가 -1이 되는 순간 탐색을 종료한다.
풀이 코드
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[][] abcd = new int[n][4];
StringTokenizer st;
for(int i=0; i<n; i++) {
st = new StringTokenizer(br.readLine());
for(int j=0; j<4; j++) {
abcd[i][j] = Integer.parseInt(st.nextToken());
}
}
int[] ab = new int[n*n];
int[] cd = new int[n*n];
for(int i=0; i<n; i++) {
for(int j=0; j<n; j++) {
ab[i*n+j]=abcd[i][0]+ abcd[j][1];
cd[i*n+j]=(abcd[i][2]+ abcd[j][3]);
}
}
Arrays.sort(ab);
Arrays.sort(cd);
int abp = 0;
int cdp = n*n-1;
long cnt=0;
while(abp<n*n && cdp >-1) {
long abv = ab[abp], cdv = cd[cdp];
long res = abv+cdv;
if(res<0) {
abp+=1;
}else if(res>0){
cdp-=1;
}else {
long xc=0, yc=0;
while(abp<n*n && abv==ab[abp]) {
abp++;
xc++;
}
while(cdp>-1 &&cdv==cd[cdp]) {
cdp--;
yc++;
}
cnt+= xc*yc;
}
}
System.out.println(cnt);
}
}'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 3020번 개똥벌레 (Java) (0) | 2021.11.11 |
|---|---|
| [BOJ] 백준 2352번 반도체 설계 (Java) (0) | 2021.11.10 |
| [BOJ] 백준 2512번 예산 (Java) (0) | 2021.11.08 |
| [BOJ] 백준 2805번 나무 자르기 (Java) (1) | 2021.11.08 |
| [프로그래머스] 위클리 챌린지 12주차 피로도 (Java) (0) | 2021.11.07 |




