#3020 개똥벌레
난이도 : 골드 5
유형 : 누적합 / 이진탐색
3020번: 개똥벌레
개똥벌레 한 마리가 장애물(석순과 종유석)로 가득찬 동굴에 들어갔다. 동굴의 길이는 N미터이고, 높이는 H미터이다. (N은 짝수) 첫 번째 장애물은 항상 석순이고, 그 다음에는 종유석과 석순이
www.acmicpc.net
▸ 문제
개똥벌레 한 마리가 장애물(석순과 종유석)로 가득찬 동굴에 들어갔다. 동굴의 길이는 N미터이고, 높이는 H미터이다. (N은 짝수) 첫 번째 장애물은 항상 석순이고, 그 다음에는 종유석과 석순이 번갈아가면서 등장한다. 아래 그림은 길이가 14미터이고 높이가 5미터인 동굴이다. (예제 그림)

이 개똥벌레는 장애물을 피하지 않는다. 자신이 지나갈 구간을 정한 다음 일직선으로 지나가면서 만나는 모든 장애물을 파괴한다.
위의 그림에서 4번째 구간으로 개똥벌레가 날아간다면 파괴해야하는 장애물의 수는 총 여덟개이다. (4번째 구간은 길이가 3인 석순과 길이가 4인 석순의 중간지점을 말한다)
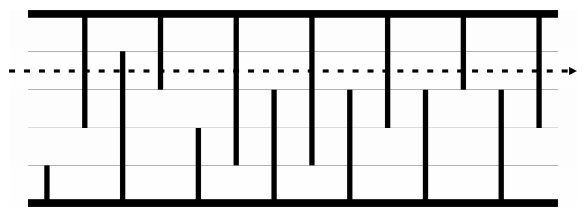
하지만, 첫 번째 구간이나 다섯 번째 구간으로 날아간다면 개똥벌레는 장애물 일곱개만 파괴하면 된다.
동굴의 크기와 높이, 모든 장애물의 크기가 주어진다. 이때, 개똥벌레가 파괴해야하는 장애물의 최솟값과 그러한 구간이 총 몇 개 있는지 구하는 프로그램을 작성하시오.
▸ 입력
첫째 줄에 N과 H가 주어진다. N은 항상 짝수이다. (2 ≤ N ≤ 200,000, 2 ≤ H ≤ 500,000)
다음 N개 줄에는 장애물의 크기가 순서대로 주어진다. 장애물의 크기는 H보다 작은 양수이다.
▸ 출력
첫째 줄에 개똥벌레가 파괴해야 하는 장애물의 최솟값과 그러한 구간의 수를 공백으로 구분하여 출력한다.
문제 풀이
완전탐색으로 각 높이에 대한 장애물의 수를 모두 파악해주는 방식을 사용하면 시간초과가 발생한다. N*H만 해도 1000억 정도의 연산이 필요하다. 그래서 이러한 효율적인 연산을 위해서 두가지 풀이방법이 있다. 첫 번째로는 이진탐색, 그리고 두 번째로는 누적합이다.
두가지 모두 풀이 아이디어는 똑같으나 탐색과정에서 차이가 있다.
이진탐색 풀이
각 층에 대한 장애물에 대한 높이 정보를 down[]과 up[]에 각각 넣는다.
- down[구간] = 장애물 높이;
- up[구간] = 장애물 높이;
위에서 저장한 데이터를 가지고 각 높이에 해당하는 각 원소의 갯수를 이진탐색으로 구해주면 된다. lower_bound를 사용하여 해당 높이보다 크거나 같은 첫번째 인덱스를 찾아 전체 크기에서 빼주면 그 구간에 존재하는 장애물의 갯수를 구할 수 있다. 물론, 각 데이터는 이진탐색을 위해 정렬해줘야 한다.
- i 높이에 존재하는 장애물의 갯수 구하기
- down : (전체 크기 - i보다 크거나 같은 첫번째 idx)
- up : (전체 크기 - (h-i+1)보다 크거나 같은 첫번째 idx)
- int conflict =binarySearch(0, n/2, i, down) + binarySearch(0, n/2, h-i+1, up);
탐색 과정에 대한 예시를 돌려보면 다음과 같다. 단순하게 높이에 대한 장애물 갯수를 카운트해 준 다음 더해주는 거라고 보면 된다. 그 다음 최솟값을 구해 해당하는 갯수를 카운트 해준다.

누적합 풀이
이는 down[]과 up[]에 각 장애물 높이를 카운트해준다. 그런 다음 해당 정보를 누적합으로 저장한다.
- down[장애물 높이]++;
- up[h-장애물 높이+1]++;
// 누적합
for(int i=1; i<=h; i++) {
down[i] += down[i-1];
}
for(int i=h; i>=1; i--) {
up[i] += up[i+1];
}
누적합에 대한 정보를 가지고 해당 구간에 존재하는 장애물의 수를 구해서 탐색해주면 된다.
- i구간에 해당하는 장애물 갯수 구하기
- down : (down 장애물 최대 갯수) - 이전 장애물 갯수(i-1)
- up : (up 장애물 최대 갯수) - 이전 장애물 갯수(i+1)
- int dif = (down[h]-down[i-1]) + (up[1]-up[i+1]);
탐색과정에 대한 예시를 돌려보면 다음과 같다. 이진탐색보다 구상하기 어렵지만 더 효율적인 탐색으로 답을 얻어낼 수 있다.

이진탐색 풀이코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int h = Integer.parseInt(st.nextToken());
int[] down = new int[n/2];
int[] up = new int[n/2];
for(int i=0; i<n/2; i++) {
int a = Integer.parseInt(br.readLine());
int b = Integer.parseInt(br.readLine());
down[i]=a;
up[i]=b;
}
Arrays.sort(up);
Arrays.sort(down);
int min = n;
int cnt=0;
for(int i=1; i<h+1; i++) {
int conflict =binarySearch(0, n/2, i, down) + binarySearch(0, n/2, h-i+1, up);
if(min == conflict) {
cnt++;
continue;
}
if(min > conflict) {
min = conflict;
cnt=1;
}
}
System.out.println(min +" " +cnt);
}
static int binarySearch(int left, int right, int h, int[] arr) {
while(left<right) {
int mid = (left+right)/2;
if(arr[mid] >= h) {
right = mid;
}else {
left = mid+1;
}
}
return arr.length-right;
}
}
누적합 풀이코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int h = Integer.parseInt(st.nextToken());
int[] down = new int[h+2];
int[] up = new int[h+2];
for(int i=1; i<=(n)/2; i++) {
int a = Integer.parseInt(br.readLine());
int b = h-Integer.parseInt(br.readLine())+1;
down[a]++;
up[b]++;
}
for(int i=1; i<=h; i++) {
down[i] += down[i-1];
}
for(int i=h; i>=1; i--) {
up[i] += up[i+1];
}
int min = n;
int cnt=0;
for(int i=1; i<h+1; i++ ) {
int dif = (down[h]-down[i-1]) + (up[1]-up[i+1]);
if(dif<min) {
min = dif;
cnt=1;
}else if(dif == min) cnt++;
}
System.out.println(min +" " + cnt);
}
}
실행결과


누적합 풀이는 굳이 lower_bound로 장애물의 갯수를 카운트하지 않고 누적합 데이터를 가지고 O(h)연산 만에 답을 얻으므로 더 빠른 실행결과를 보여준다.
'Dot Algo∙ DS > PS' 카테고리의 다른 글
| [BOJ] 백준 2143번 두 배열의 합 (Java) (0) | 2021.11.13 |
|---|---|
| [BOJ] 백준 2467번 용액 (Java) (0) | 2021.11.12 |
| [BOJ] 백준 2352번 반도체 설계 (Java) (0) | 2021.11.10 |
| [BOJ] 백준 7453번 합이 0인 네 정수 (Java) (0) | 2021.11.09 |
| [BOJ] 백준 2512번 예산 (Java) (0) | 2021.11.08 |




